Stefan Schmerler - Softwaretest in der Praxis

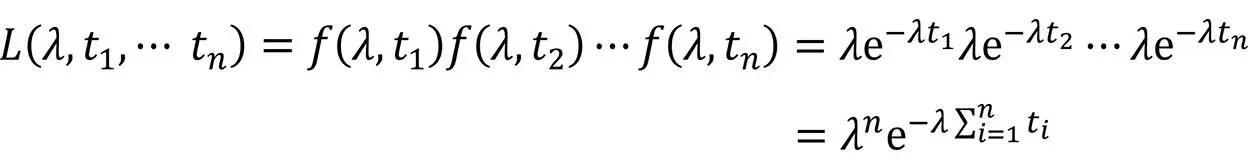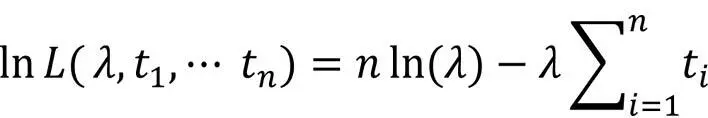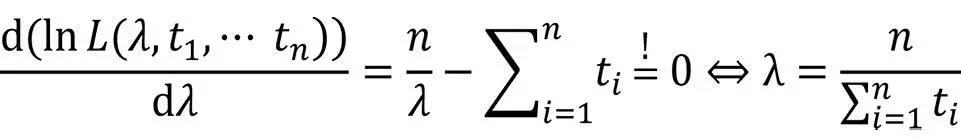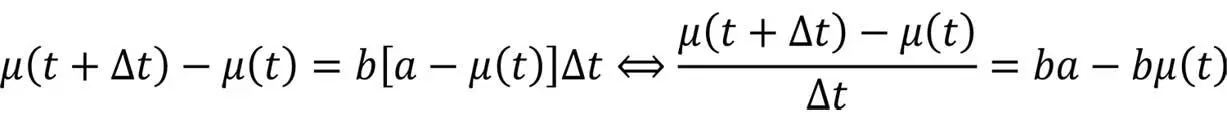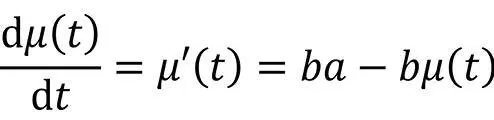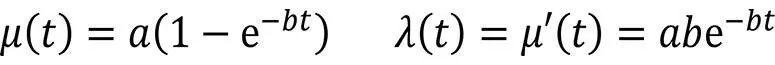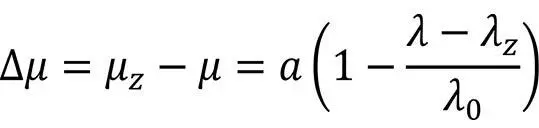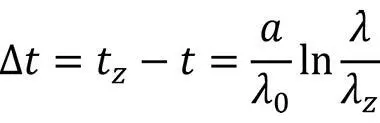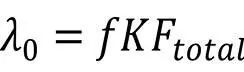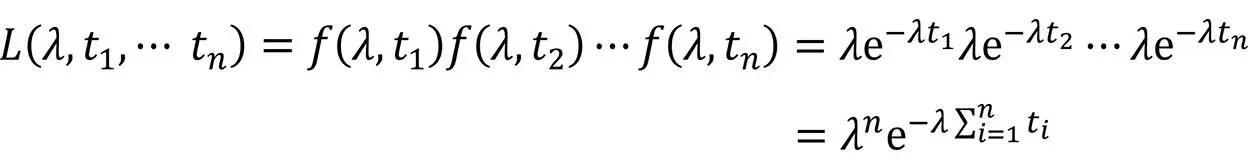
Aufgrund der Monotonie der Logarithmusfunktion besitzen L und ln(L) dieselben Extrema:

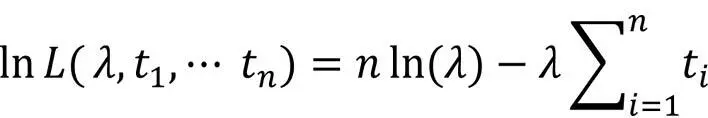
Das Maximum der Likelihood-Funktion ergibt sich zu:

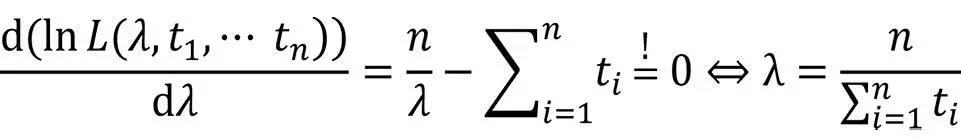
2.2.6 Zuverlässigkeitsmodell nach Musa

Auch wenn dieses Verfahren der Zuverlässigkeitsmodellierung schon etwas betagt ist, kann man beim Zuverlässigkeitsmodell nach Musa sehr schön Vorgehensweise und Nutzen von Zuverlässigkeitsmodellen erkennen.

Welchen Nutzen bietet dieser Ansatz?

Es gilt wiederum, aus Beobachtungen des Ausfallverhaltens in einer Beobachtungsphase bzw. während der Entwicklung auf das künftig zu erwartende Ausfallverhalten zu schließen. Musa liefert am Ende unter bestimmten Prämissen quantitative Aussagen hierfür und sogar eine Abschätzung für den Aufwand, der noch in den Test investiert werden muss, um ein bestimmtes Ausfall-/Reifegradziel zu erreichen. Dies ist schon allerhand für eine in der Praxis doch eher von Intuition geprägten Disziplin wie dem Softwaretest.

Doch beginnen wir mit den Prämissen. Die Annahme ist, dass ein Softwaresystem aufgrund von Fehlern zu (zumindest aus Anwendersicht) zufälligen Zeitpunkten t1, t2 usw. ausfällt. Um implementierungsunabhängiger zu werden, ist unter Zeit immer CPU-Zeit zu verstehen.

Prämissen für diesen Ansatz

Musa nimmt ferner an, dass die Anzahl der in einem Zeitintervall Δt beobachteten Ausfälle proportional zur Anzahl der zu dieser Zeit in der Software vorhandenen Fehler ist. Die bis zum Zeitpunkt t ≥ 0 beobachtete Anzahl von Ausfällen wird in μ(t) beschrieben und es gilt:

▶μ(t) steigt monoton mit μ(0) = 0.

▶Für die Anzahl der insgesamt erwarteten Ausfälle gilt μ(t → ∞) = a, mit a als Anzahl der im SUT beobachtbaren Fehler.

Die Anzahl der in Δt beobachteten Ausfälle ist proportional zu Δt und zur Zahl der noch nicht entdeckten Fehler – dies in Formeln ausgedrückt bedeutet mit a und b als Geradenparameter (Proportionalität):

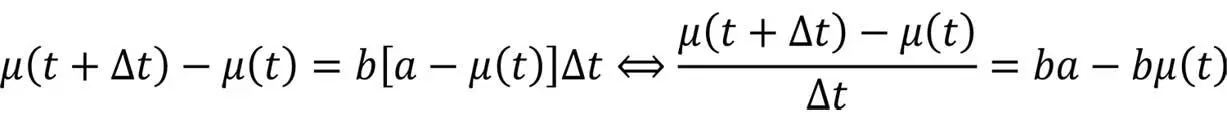
Für Δt → 0 ergibt sich

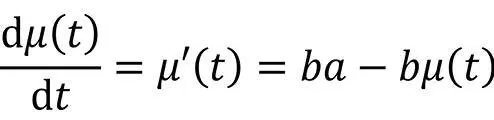
Mit μ(0) = 0 und μ(t → ∞) = a findet man als Lösung der DGL

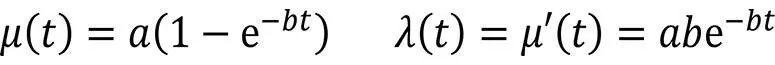
Wie viele Fehler sind noch zu beheben,

bis ein Zielreifegrad erreicht wird?

Weitere Umformungen, die ich uns hier ersparen möchte, liefern zwei Ergebnisse: Falls λ die aktuelle Ausfallrate der Software ist sowie λ0 diejenige zum Zeitpunkt 0 (zu Beginn von Test und Fehlerbeseitigung) und für die Ausfallrate ein Ziel λZ definiert ist, müssen bis zur Erreichung dieses Ziels noch Δμ zusätzliche Ausfälle beobachtet und deren Ursachen behoben worden sein (ohne Herleitung):

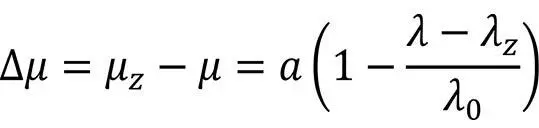
Für die zusätzliche Zeit Δt bis zur Erreichung dieses Ziels gibt Musa an (hier auch ohne Herleitung):

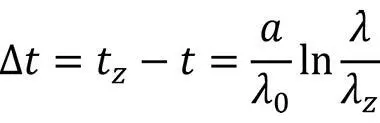
… und wie lange dauert dies?

Dies sind recht interessante Ergebnisse. Man kann auf diese Weise etwas konkretere Vorstellungen dafür erhalten, wie weit man im Absicherungsprozess bislang vorangekommen ist und wie lange es noch dauern könnte, um ein definiertes Reifegradziel λZ zu erreichen.

Das vorgestellte Modell besitzt zwei Parameter, die für einen spezifischen Anwendungsfall vorliegen müssen:

▶a: Die Gesamtzahl der beobachteten Ausfälle für t → ∞

▶λ0: Die Ausfallrate zu Beginn. Für sie wird später noch eine Abschätzung angegeben.

Auch zur Bestimmung oder wenigstens guten Abschätzung dieser Parameter hat sich Musa Gedanken gemacht – auch hierzu gleich mehr.

Nachbesserung bei den Prämissen

Eine Verbesserung dieses Ansatzes adressiert den Umstand, dass nicht jeder Ausfall zu einer Fehlerkorrektur führt – dies war aber eine Grundprämisse von Musa. In der Realität werden manche Fehler toleriert aufgrund zu geringer Fehlerwirkung und bei einem Teil der Fehlerkorrekturen werden gar neue Fehler in das System eingebracht.

Beobachtbarkeit von Fehlern

Zudem ist eine Prämisse, dass die Anzahl der in einem System vorhandenen Fehler gleich der Anzahl der Ausfälle für t → ∞ ist, genauer betrachtet unhaltbar. Nicht jeder Fehler ist beobachtbar! Auch hier muss daher noch nachgebessert werden. Musa tut dies, indem er einen Faktor B einführt als Verhältnis der für t → ∞ gefundenen und korrigierten Fehler fk zur Anzahl aller beobachtbaren Fehler a: B = fk /a. Wird jeder beobachtete Fehler durch die Korrekturmaßnahme auch korrigiert, so ist B = 1. Allerdings führt nicht jede Korrektur zur Fehlerbeseitigung, manchmal werden sogar bei der Korrektur neue Fehler eingebracht. Es wird für B auf Basis empirischer Untersuchungen ein Wert von 0,955 angegeben.

5% der Fehlerkorrekturen sind erfolg-

los oder selbst fehlerbehaftet.

Dies bedeutet nichts anderes, als dass etwa 5 % aller Fehlerkorrekturen erfolglos sind oder durch die Korrektur neue Fehler eingebracht wurden. Geht man davon aus, dass für t → ∞ alle in einer Software vorhandenen Fehler Ftotal aufgrund von Ausfällen gefunden und korrigiert werden, so ist mit der Anzahl an Ausfällen Fein software-

a zu rechnen: a = Ftotal /B. Es bleibt noch der Parameter λ0, für den man nach Musa die Abschätzung abgeben kann

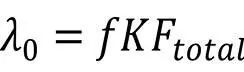
wobei für Ftotal die in Abb. 2-7 aufgeführten Abschätzungen gegeben werden:

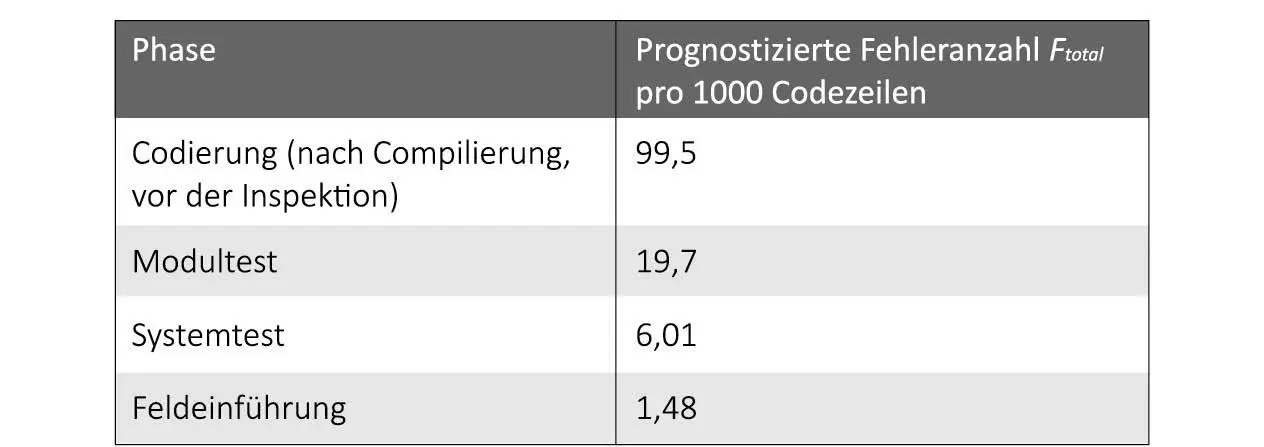
Abb. 2-7: Abschätzung für Ftotal

Bestimmung von f

Der Performancefaktor f wird durch Musa angegeben durch das Verhältnis der Ausführungsgeschwindigkeit (in Objektcode-Anweisungen pro Zeiteinheit) zum Softwareumfang (in Objektcode-Instruktionsanzahl).

Bestimmung von K

Zuletzt benötigen wir noch Werte für den Parameter K, der folgende Faktoren erfasst:

▶Nicht jede (fehlerhafte) Anweisung wird bei jeder Programmausführung durchlaufen.

▶Nicht jede Ausführung einer fehlerhaften Anweisung führt zu einem Fehlverhalten, da das Auftreten mancher Fehler an bestimmte Datenwerte gebunden ist.

Hinsichtlich des Parameters K wurden einige empirische Untersuchungen angestellt, nach welchen K unabhängig vom Codeumfang mit einem durchschnittlichen Wert von 4,2 . 10–7 angegeben werden kann.