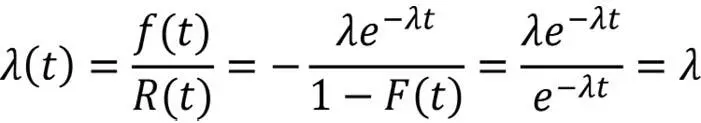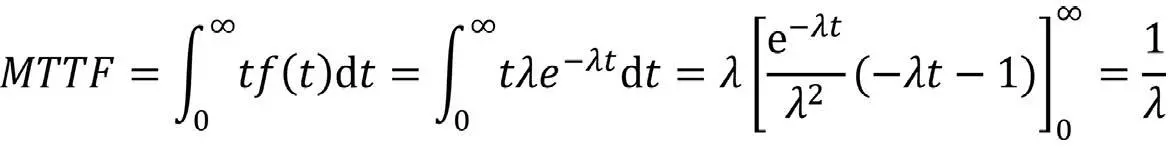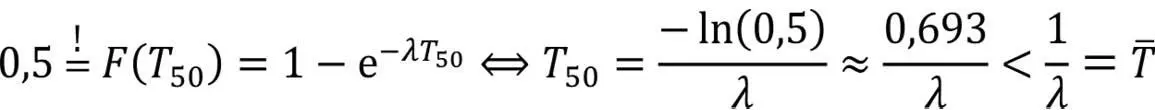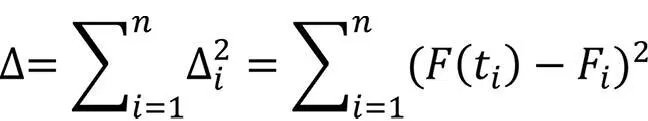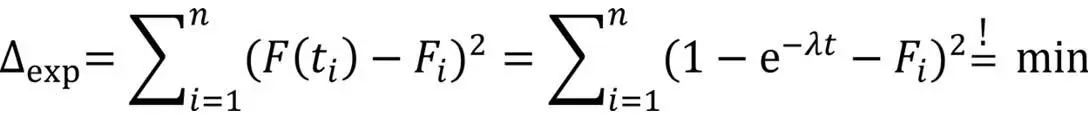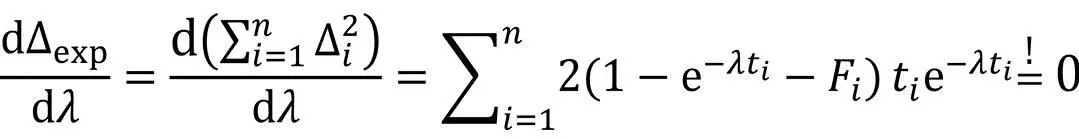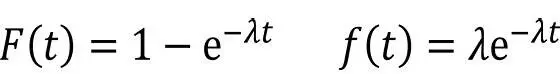Stefan Schmerler - Softwaretest in der Praxis

Ausfallverhaltens von Software

Leider haben wir aber noch keine Dichte der Ausfallfunktion f (t) bzw. Verteilungsfunktion für das Ausfallverhalten für Software, um diese Größen auswerten zu können. Es ist auch nicht klar, ob es überhaupt eine dedizierte Ausfallfunktion für Software gibt. Wir kennen aber die Randwerte F(0) = 0 und F(t → ∞) = 1 und treffen hier die Annahme einer Exponentialfunktion F(t) = 1 – e-λ(t) mit dem Parameter λ(t) (Abb. 2-4).

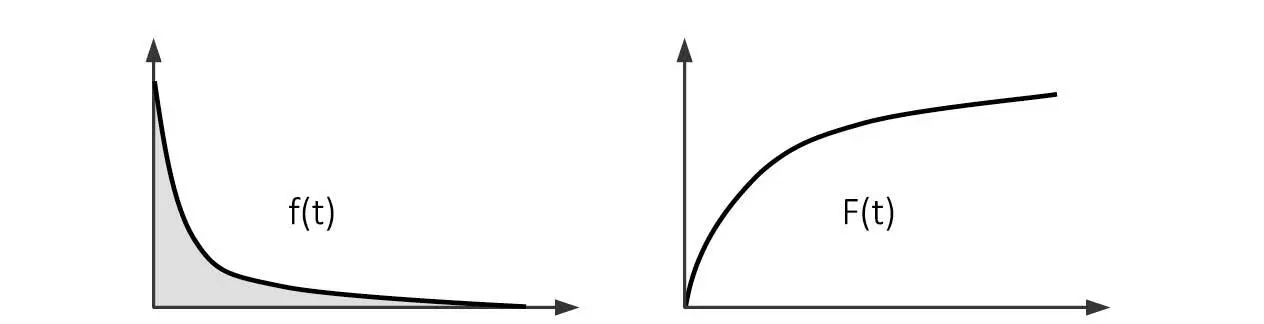
Abb. 2-4: Annahme exponentialverteilter Ausfallfunktion für Software

Unter dieser Annahme (deren Korrektheit wir im Übrigen noch beurteilen werden) können wir unsere Kenngrößen Lebensdauer und MTTF nun in alleiniger Abhängigkeit vom Parameter Ausfallrate λ ausdrücken.

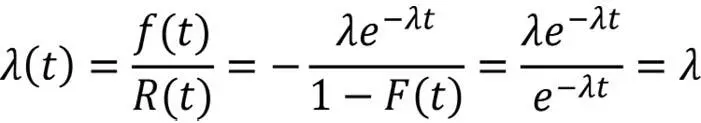
Dies ist interessant: Unter der Annahme einer exponentialverteilten Ausfallfunktion verliert die Ausfallrate ihre Abhängigkeit von der Zeit, sie wird zeitlich konstant.

zeitunabhängiges Ausfall-

verhalten von Software

Dies ist ein Indiz dafür, dass unsere Annahme einer exponentialverteilten Ausfallfunktion, die wir ja noch beurteilen wollten, korrekt war. In der Tat kann das Ausfallverhalten von Software ja nicht zeitabhängig sein – Software verändert sich nicht oder verliert ihren Reifegrad, je länger sie benutzt wird. Ganz im Gegensatz zu Glühbirnen oder Halbleitern in der Mikroelektronik. Dort haben wir es mit einem ausgeprägt zeitabhängigen Ausfallverhalten zu tun: Wir erinnern uns an die Badewannenkurve des Ausfallverhaltens von Halbleitern, das ganz zu Beginn (Produktionsfehler) und nach einigen Jahren Betrieb (Halbleiteralterung) ansteigt und in den zwischenzeitlichen Nutzungsjahren konstant niedrige Werte aufweist.

Die MTTF für Softwareausfälle wird damit ebenfalls zeitunabhängig:

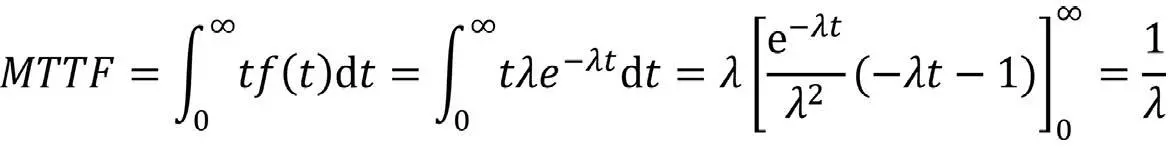
Interessant ist noch die Ausfallzeit T50 , also diejenige Zeit, zu der die Wahrscheinlichkeit eines Softwareausfalls 50 % beträgt: F(T50 ) = 0,5:

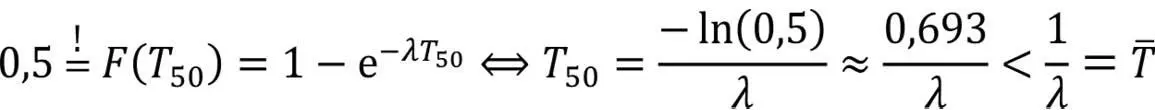
unterschiedliches Ausfallverhalten

von Hardware und Software

Bemerkenswerterweise ist diese Zeit nicht der Erwartungswert der Lebensdauer (also die mittlere Lebensdauer) – sie ist deutlich kleiner, d. h. die Überlebenswahrscheinlichkeit 50 % wird bereits deutlich früher erreicht als der mittleren Lebensdauer entspricht.

Das unterschiedliche Ausfallverhalten von Hardware und Software wird in der folgenden Darstellung illustriert. Die zeitabhängige Ausfallrate λ bei Hardware führt dazu, dass im Laufe der Zeit neue Fehler hinzukommen. Alle zu einem Zeitpunkt vorhandenen Fehler sind immer sichtbar, d. h. beobachtbar und zeigen Fehlerwirkung (linkes Bild in Abb. 2-5).

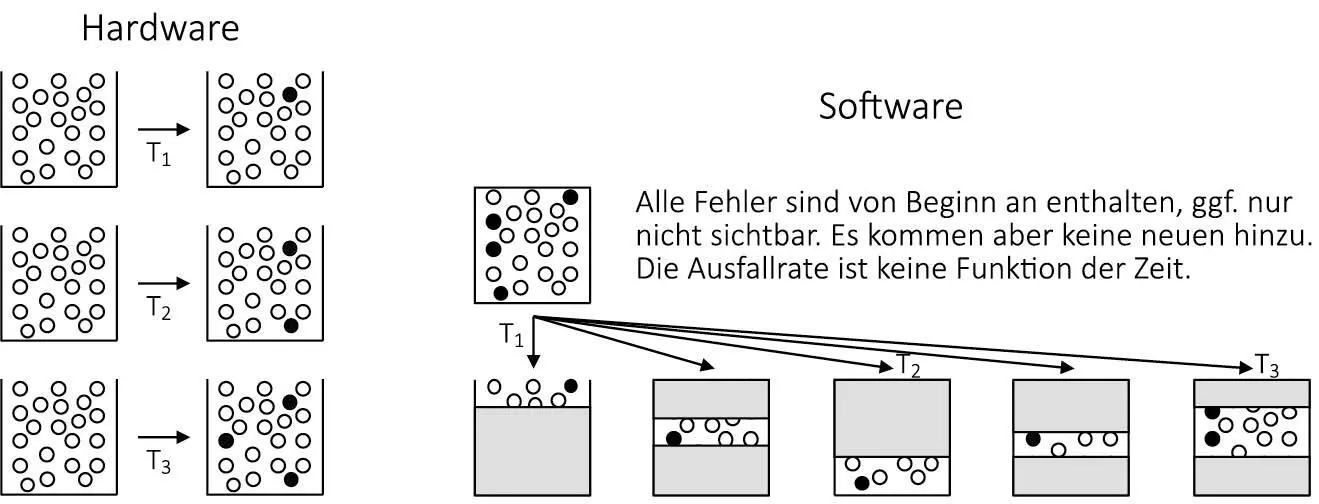
Abb. 2-5: Zeitabhängigkeit von Ausfallraten bei HW und SW

2.2.5 Stochastische Zuverlässigkeitsmodelle für Software

Musa, Jelinski-Moranda,

Littlewood-Verrall

Seit den 1970er Jahren wurde eine Reihe von Zuverlässigkeitsmodellen für Software entwickelt. Verbreitet und noch immer anwendbar sind die Modelle nach John D. Musa [8], das Jelinski-Moranda-Modell [9] und auch das Littlewood-Verrall-Modell [10].

Allen gemeinsam ist das Vorgehen, die freien Parameter des Zuverlässigkeitsmodells so zu bestimmen, dass das Verhalten des Modells möglichst nahe am zu beobachtenden Ausfallverhalten in der Realität liegt. Hierfür gibt es mehrere Ansätze, zwei davon werden im Folgenden vorgestellt.

Im Verfahren der kleinsten Fehlerquadrate werden die Quadrate der Abweichungen zwischen jeder Beobachtung und dem Wert, den das Zuverlässigkeitsmodell an dieser Stelle liefert, durch Parameteradjustierung minimiert.

Maximiert wird die Wahrschein-

lichkeit für ähnliches Verhalten.

Im Maximum-Likelihood-Verfahren werden freie Parameter so gewählt, dass die Wahrscheinlichkeit maximiert wird, ein zur vorliegenden Beobachtung ähnliches Verhalten zu erzielen.

Wer auf den ersten Blick keinen wesentlichen Unterschied zwischen den beiden Arten der Parameterbestimmung erkennt, dem sei dies anhand eines kleinen Beispiels erläutert. Wir betrachten das Ausfallverhalten und die Lebensdauer T von N Komponenten (man könnte sich wieder 1000 Glühbirnen vorstellen). Nach und nach fallen einzelne Komponenten aus und nach langer Zeit ist zu erwarten, dass n = N Komponenten ausgefallen sind. Dies ist das beobachtete Ausfallverhalten:

Abb. 2-6: Beobachtetes zeitliches Ausfallverhalten

Beispiel für kleinste Fehlerquadrate

Nach der Methode der kleinsten Fehlerquadrate sollen nun die Parameter der Verteilungsfunktion bestimmt werden. Fi bezeichnen hier die Werte dieser empirischen Verteilungsfunktion entsprechend der obigen Tabelle, wohingegen F(ti) den Wert repräsentiert, den hier unser Zuverlässigkeitsmodell liefert und dessen Parameter wir bestimmen wollen. Die Methode der kleinsten Fehlerquadrate ergibt

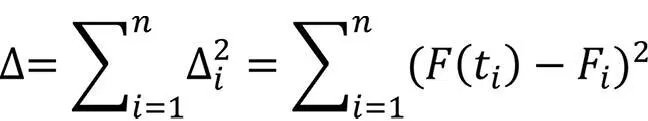
Annahme: Exponential-

verteiltes Ausfallverhalten

Da wir ein Zuverlässigkeitsmodell für Software parametrieren, wird für das Ausfallverhalten eine Exponentialverteilung angesetzt. Die Minimierung der Differenzfunktion Δexp ergibt unter diesen Randbedingungen das folgende Gleichungssystem:

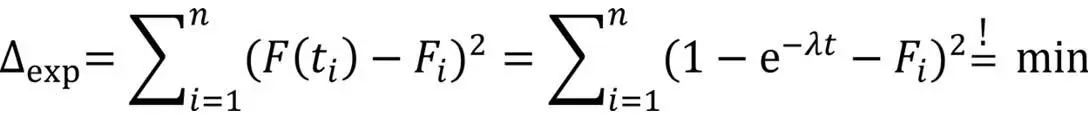
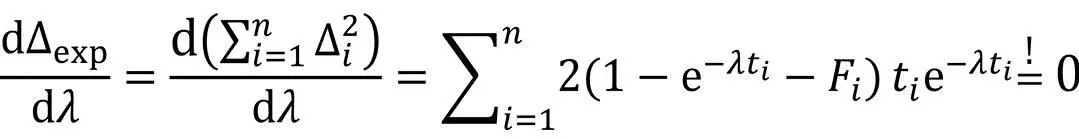
Ein numerisches Lösungsverfahren liefert die Lösung λ = 3,93 . 10-5/h. Die Summe der Fehlerquadrate beträgt dann 2,81 . 10-3.

dasselbe Beispiel für

Maximum-Likelihood

Wenden wir auf unser kleines Beispiel aber das Maximum-Likelihood-Kriterium an, so werden die Parameter der Verteilung so ermittelt, dass die Wahrscheinlichkeit maximiert wird, über die Verteilungsfunktion eine möglichst ähnliche Ausfallcharakteristik zu erhalten wie das beobachtete Verhalten.

Likelihood-Funktion

Die Likelihood-Funktion L muss also das Produkt der Dichten an den beobachteten Ausfallzeitpunkten sein – in gleicher Weise wie Wahrscheinlichkeiten multipliziert werden, wenn Ereignisse gemeinsam eintreten sollen. Ihr Wert ist proportional zu der Wahrscheinlichkeit, Ausfallzeitpunkte zu beobachten, die von der vorliegenden Beobachtung maximal Δt abweichen. Diese gilt es zu maximieren. Für das Ausfallverhalten wird wieder eine Exponentialverteilung angenommen.

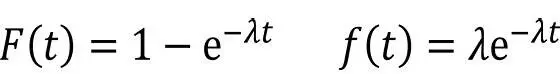
Für die Likelihood-Funktion L bei n beobachteten Ausfallzeiten ergibt sich also: