Stefan Schmerler - Softwaretest in der Praxis

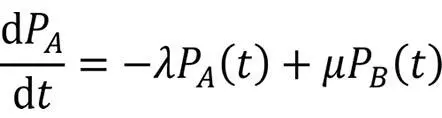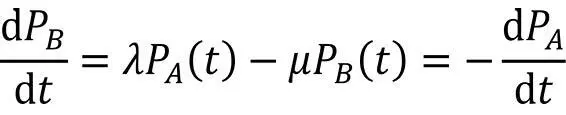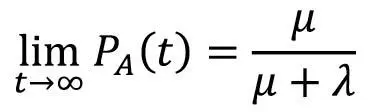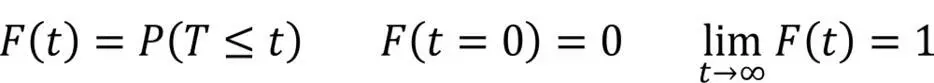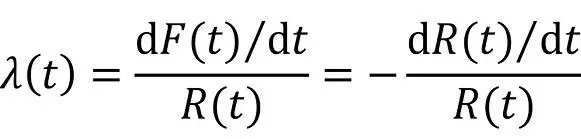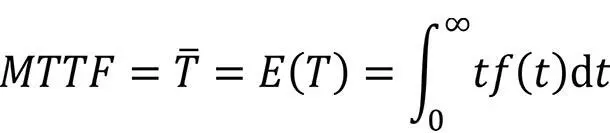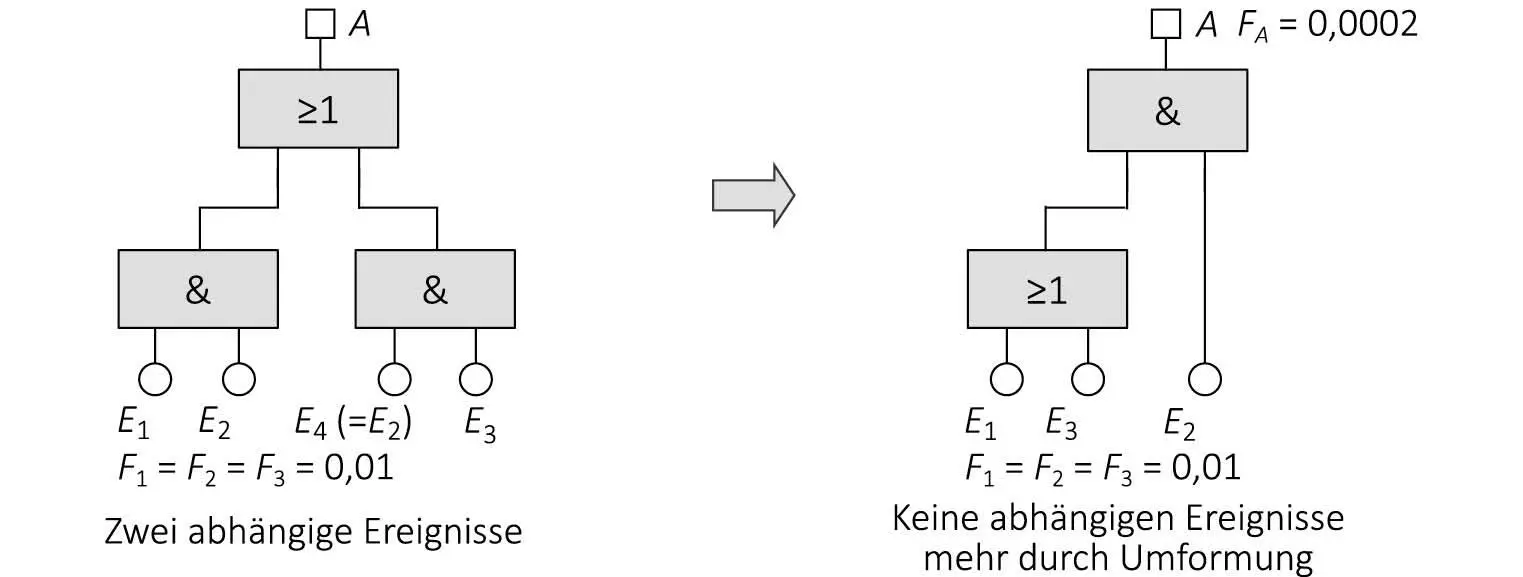
Abb. 2-2: Boolesche Umformungen sind hilfreich.

2.2.3 Markov-Modellierung

Das Systemverhalten wird als sto-

chastischer Prozess verstanden.

Eine weitere gängige Methode der Zuverlässigkeitsmodellierung ist die Markov-Modellierung. Sie beschreibt das Systemverhalten mit Zustandsautomaten als stochastischen Prozess. Ziel ist es, die Wahrscheinlichkeit für das Eintreten zukünftiger Ereignisse anzugeben. Fasst man das Auftreten eines Fehlers als Ereignis auf, dessen Wahrscheinlichkeit für die Beurteilung des Reifegrads von Bedeutung ist, kann eine Analyse von Markov-Modellen wertvolle Aussagen liefern. Insbesondere ist die Frage interessant, mit welcher Wahrscheinlichkeit unser System denn nun defekt ist, wenn man es zu einem zufälligen Zeitpunkt betrachtet.

zufällige Zustandsübergänge

Bei einer Markov-Kette besteht die Möglichkeit, die Kanten eines Zustandsautomaten mit Wahrscheinlichkeiten zu versehen und somit zufällige Zustandsänderungen im Modell zu hinterlegen.

Dies gestattet die Beschreibung eines zufälligen Ausfallverhaltens mittels der statistischen Ausfallrate λ und der Reparaturrate μ. Im Beispiel ist der intakte Systemzustand mit A bezeichnet, der Systemausfallzustand mit B.

Ausfallrate λ

Die Ausfallrate λ ist zu verstehen als Grenzwert der in einem Zeitintervall Δt ausgefallenen Einheiten bezogen auf die zu Beginn noch funktionsfähigen Einheiten R(t) für Δt → 0.

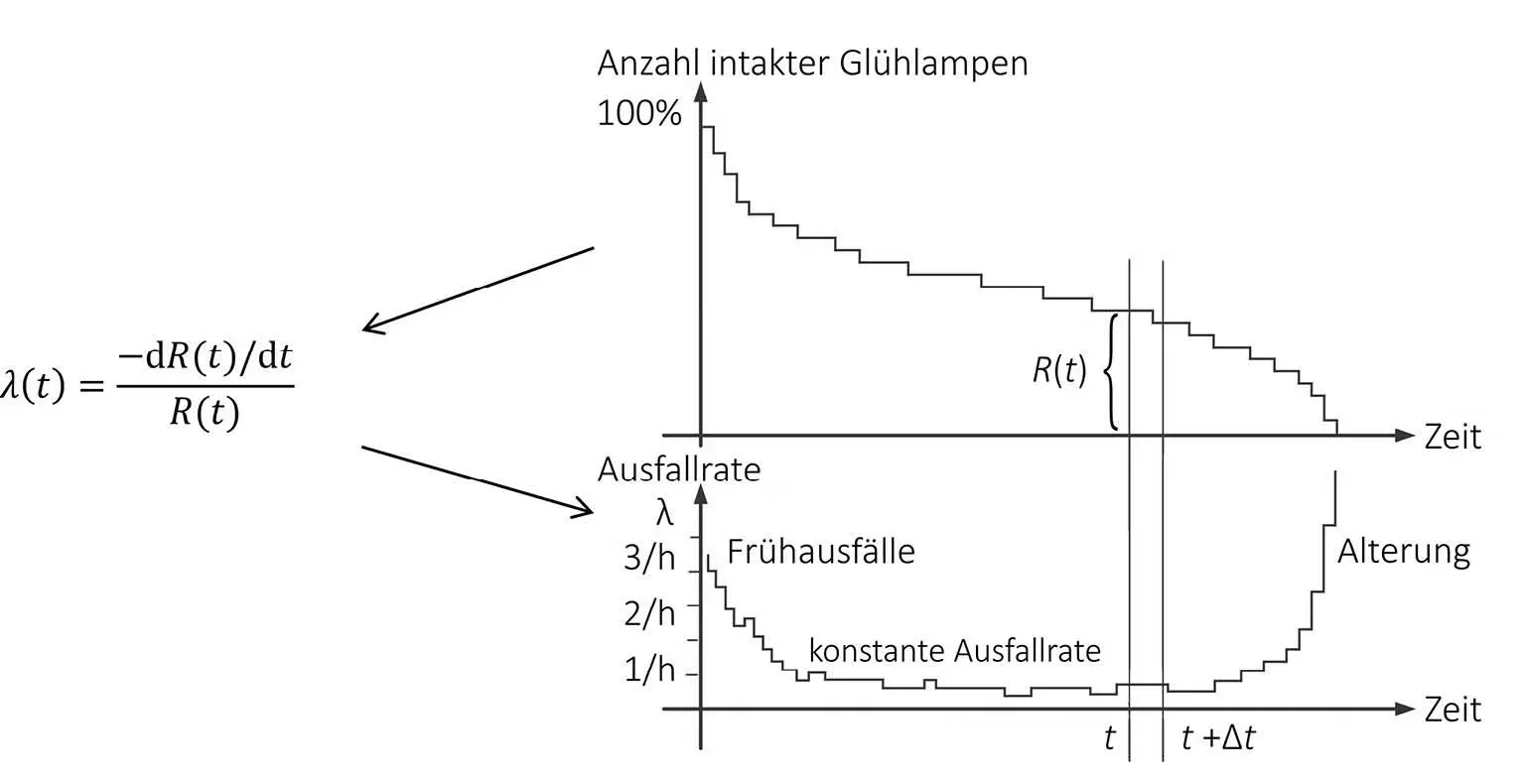
Abb. 2-3: Illustration der Ausfallrate am Beispiel von Glühbirnen

Es handelt sich um die bedingte Wahrscheinlichkeit, dass ein System, das bis zum Zeitpunkt t ausfallfrei war, auch noch das Zeitintervall Δt ohne Ausfall übersteht.

Reparaturrate μ

Die Reparaturrate μ ist entsprechend zu verstehen als Anzahl der Reparaturen bezogen auf die Zeiteinheit. Für die zeitliche Veränderung der Aufenthaltswahrscheinlichkeit in den Zuständen A oder B gilt schließlich:

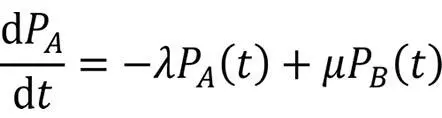
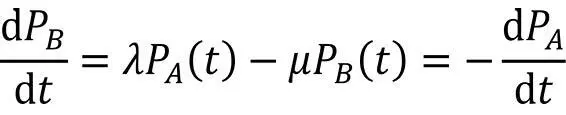
Mit welcher Wahrscheinlichkeit ist ein

System defekt, wenn man es zu einem

zufälligen Zeitpunkt betrachtet?

Die erste Gleichung bedeutet, dass die Änderung der Wahrscheinlichkeit, dass sich das System in Zustand A befindet, also funktionstüchtig ist, verursacht werden kann durch einen Wechsel von B (»defekt«) nach A (also positives Vorzeichen) abzüglich einer Bewegung von A nach B (negatives Vorzeichen). Eine ähnliche Interpretation findet sich für die zweite Gleichung, die eine Veränderung des Systems beschreibt, das sich in Zustand B befindet.

Es bleibt noch festzustellen, dass PA(t) + PB(t) = 1 gilt, da sich das System stets in einem der beiden Zustände befinden muss. Ohne Herleitung ergibt sich nach Lösung des Differenzialgleichungssystems für die Wahrscheinlichkeit, ein System mit gegebener Ausfall- und Reparaturrate im fehlerfreien Zustand anzutreffen, der Ausdruck

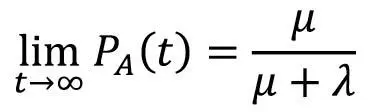
Wir haben eine quantitative

Aussage über die Zuverlässigkeit!

Auch dies kann eine interessante Aussage über die Zuverlässigkeit von reparierbaren Systemen sein, wenn Ausfall- und Reparaturrate bekannt sind.

2.2.4 Stochastische Zuverlässigkeitsanalyse für Software

Wir versuchen, Aussagen über das zu-

künftige Ausfallverhalten zu erhalten.

Mit Zuverlässigkeitsmodellen versucht man, durch Beobachtung des Ausfallverhaltens über einen bestimmten Zeitraum Prognosen über das zukünftig zu erwartende Ausfallverhalten zu erlangen. Zuverlässigkeitsmodelle werden häufig durch Kenngrößen parametriert, wobei die Parameter in einer Beobachtungsphase stochastisch ermittelt werden.

Fällt Software wirklich zufällig aus?

Die Aussagekraft der Ergebnisse von Softwarezuverlässigkeitsmodellen hängt natürlich stark von der Qualität der zugrunde liegenden Modelle ab, besitzt aber einen präventiven Charakter. Die Frage ist dabei allerdings, inwieweit Software überhaupt stochastisches Ausfallverhalten aufweist. Ein spontaner – also rein zufälliger – Ausfall ist zwar nicht möglich und Software verschleißt auch nicht, dennoch erscheint der Ausfall aus Sicht des Benutzers oft als durchaus zufällig und unmotiviert. Viele Softwarefehlerzustände, wie z. B. nichtinitialisierte Zeiger in der Sprache C, treten quasi zufällig auf, zumindest abhängig von zufälligen Speicherinhalten im nichtinitialisierten Arbeitsspeicher. Auch die Art und Intensität der Benutzung von Software beeinflusst die Häufigkeit, mit der vorhandene Fehler tatsächlich zutage treten.

Wenn Software aber stochastisches Ausfallverhalten aufweist, können Software und Hardware mit analogen Zuverlässigkeitsmodellen betrachtet werden, d. h., wir können Kenngrößen übertragen, die wir aus der Hardwarezuverlässigkeit kennen.

Lebensdauer T - wir ziehen eine Analogie

zwischen Software und Glühbirnen.

Interessant wäre zunächst die Lebensdauer T. Hinsichtlich der Lebensdauer als stochastischer Kenngröße bemühen wir hier die Analogie zu einem Kollektiv von sagen wir N = 1000 Glühbirnen, die eine gewisse Lebensdauer bis zu ihrem ersten (und letzten) Ausfall aufweisen. Bei N Glühbirnen ergibt sich eine Wahrscheinlichkeitsverteilungsfunktion F(t) für den Ausfall. Die Lebensdauer T repräsentiert hierbei die Zufallsvariable und F(t) die zugehörige Verteilungsfunktion. Es gilt: F(t1) ist die Wahrscheinlichkeit, dass der Ausfall in 0 ≤ t ≤ t1 erfolgt ist, die Lebensdauer also T ≤ t1 beträgt, und es ergibt sich

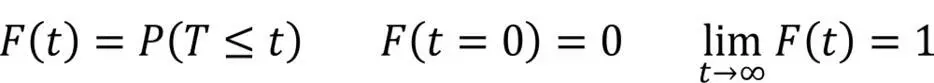
Überlebenswahrscheinlichkeit R(t)

R(t) bezeichnet die Überlebenswahrscheinlichkeit 1 − F(t), d. h. die Wahrscheinlichkeit, dass bis zum Zeitpunkt t noch kein Ausfall aufgetreten ist. Da F(t) die Verteilungsfunktion einer Zufallsvariable ist, ergibt sich als Wahrscheinlichkeitsdichtefunktion f (t) = dF(t) / dt.

Ermittlung der Ausfallrate λ

Des Weiteren lässt sich eine Ausfallrate λ(t) bestimmen als Grenzwert der in einem Zeitintervall Δt ausgefallenen Einheiten pro Zeiteinheit bezogen auf die zu Beginn von Δt noch funktionsfähigen Elemente R(t) für Δt → 0:

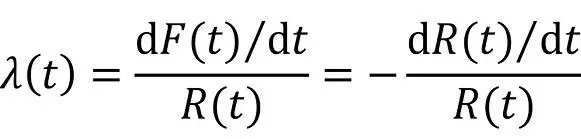
Die MTTF bzw. Mean Time between Failure (MTBF) bei reparierbaren Systemen ergibt sich gemäß der Definition des stochastischen Erwartungswerts E(T ) zu

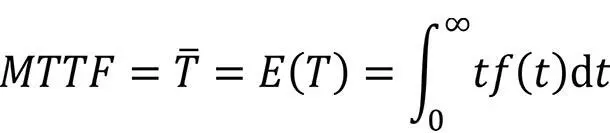
Annahme eines exponentialverteilten