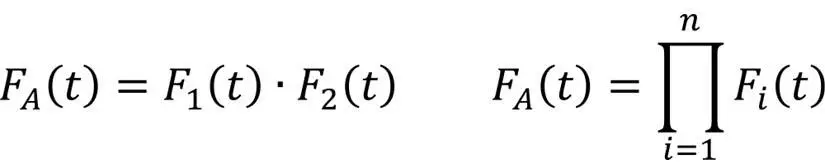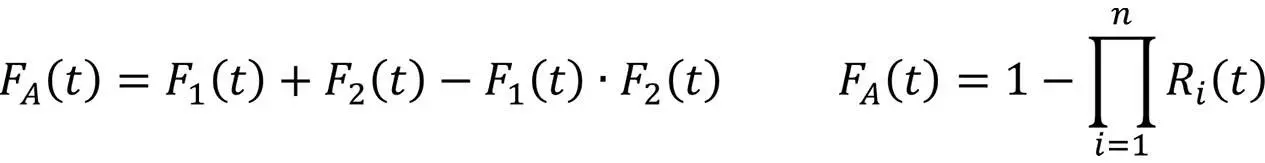Stefan Schmerler - Softwaretest in der Praxis

▶FMECA (Failure Mode, Effects and Criticality Analysis): IEC 6081206

▶Zuverlässigkeitsblockdiagramm: IEC 6107806

▶FTA (Fault Tree Analysis/Fehlerbaumanalyse): DIN 2542490

▶Markov-Analysen: IEC 6116506

Auf einen Teil dieser Methoden wird im weiteren Verlauf noch eingegangen. Allen gemein ist das Ansinnen, Struktur und Metrik in den Beurteilungsprozess für die Zuverlässigkeit von Software zu bringen.

2.2.1 Software-FMECA

Bei der Software-FMECA handelt es sich um eine präventive Methode zur Identifikation von Fehlern, ihrer Risiken und Auswirkungen. Ziel ist die Quantifizierung von Risiken sowie das Finden geeigneter Abhilfemaßnahmen. Die Durchführung einer Software-FMECA erfolgt in einer Abfolge von vier Schritten, die im Folgenden dargestellt werden. Die Einführung einer Risikoprioritätszahl hilft bei der quantitativen Bewertung von Risiken.

1.Ausfallanalyse: Hier macht man sich Gedanken über die wesentlichen Ausfälle, die das System zeigen könnte. Insbesondere die Fragestellung »Was darf unter keinen Umständen passieren?« ist hier sehr hilfreich.

2.Dann erfolgt für jedes dieser Risiken eine Risikobewertung durch Ermittlung einer Risikoprioritätszahl (RPZ).

RPZ = Eintrittswskt × Gewicht der Folgen × Wskt des Nichtentdeckens

Für jeden der drei Einflussfaktoren wird ein Wert zwischen 1 und 10 angesetzt (1: niedrig/gering, 10: hoch), sodass sich für jedes der Risiken eine RPZ im Bereich 1 bis 1000 ergibt.

3.Für jedes der Risiken sind Maßnahmenvorschläge zu erarbeiten, beginnend bei Risiken mit hoher RPZ. Dies sind die Risiken, die z. B. eine hohe Eintrittswahrscheinlichkeit bei moderatem Schaden aufweisen bzw. immensen Schaden bei moderater Eintrittswahrscheinlichkeit.

4.Die RPZ wird nach Einarbeiten der Maßnahmen erneut analysiert.

Oftmals wird in der Praxis bei größeren Entwicklungsprojekten eine Software-FMECA vorgeschrieben. Dies ist ein einfaches Hilfsmittel und bringt Systematik und vor allem Metrik in den Reifegradprozess. Man ist gezwungen, sich ggf. noch vor Beginn der Entwicklung Gedanken über mögliches Fehlverhalten zu machen und Gegenmaßnahmen vorzusehen. Auch hier möchte man die Vorteile der Prävention nutzen und ein System nicht nachträglich durch aufgetretene Fehler kennenlernen. Die FMECA zielt auf die Erkennung gravierender Mängel ab und hat sich in der Praxis sehr bewährt.

2.2.2 Fehlerbaumanalyse

Die Fehlerbaumanalyse gehört zur Gruppe der qualitativen wie auch zu den quantitativen Analysemethoden. Sie kommt zum Einsatz bei sicherheitskritischen, komplexen Systemen.

komplexe Fehlermechanismen herunter-

brechen auf beherrschbare Problemgrößen

Das Prinzip der Fehlerbauanalyse ist es, komplexe funktionale Zusammenhänge, über deren Ausfallverhalten man keine klaren Aussagen treffen kann, aufzubrechen in kleinere, beurteilbare Einheiten und die Teilergebnisse zu einer Gesamtaussage zu aggregieren. Hochkomplexe Systeme werden auf diese Weise in ihrem Ausfallverhalten quantitativ beurteilbar.

Eine Besonderheit der Fehlerbaumanalyse ist die Möglichkeit der grafischen Repräsentation, um den Zusammenhang zwischen Fehlerursache und -wirkung zu veranschaulichen.

Zum Einsatz kommen nach DIN 25424 genormte Symbole als Elementarbausteine, aus denen der Baum des Gesamtsystems sukzessive zusammengesetzt wird (Abb. 2-1).

die elementaren Verknüpfungen

Die Grundlogik für die drei elementaren Verknüpfungen NICHT, ODER und UND ist jeweils, dass eine Fehlerwirkung (A = 1) eintritt, falls die verknüpften Ereignisse die jeweils genannte Eigenschaft erfüllen.

Durch Aufbau komplexer Strukturen aus Elementarbausteinen mit bekanntem Ausfallverhalten kann also modelliert werden, wie Fehler sich in einem System fortpflanzen bzw. ausbreiten. Am Ende steht ein Blick auf das Ausfallverhalten des Gesamtsystems. Dies sind interessante Erkenntnisse, insbesondere, wenn bereits Vorkehrungen zur aktiven Fehlererkennung und -beseitigung im laufenden Betrieb vorgesehen sind.

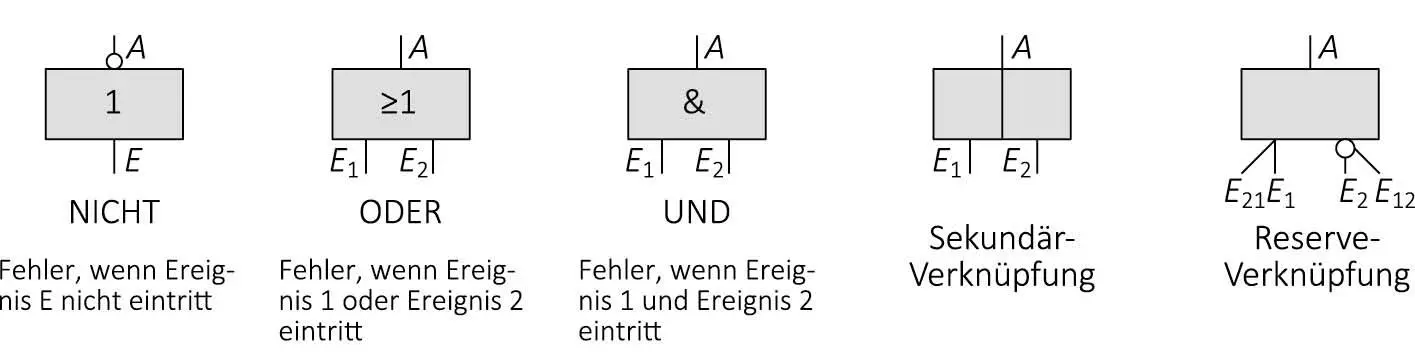
Abb. 2-1: Symbole Fehlerbaumanalyse gemäß DIN 25424

Sekundärverknüpfung für Fehler, die

sich nur möglicherweise fortpflanzen

Vor diesem Hintergrund sind auch die beiden letzten Elementarbausteine in Abb. 2-1 zu sehen. Bei der Sekundärverknüpfung gilt folgende Logik: Falls sich der Wert an Eingang E1 einer Sekundärverknüpfung von logisch 0 nach 1 ändert, so wird mit einer an Eingang E2 angegebenen Dauer und Wahrscheinlichkeit der Wert des Ausgangs auf logisch 1 gesetzt. Es werden also Sekundärausfälle beschrieben, die nur möglicherweise von Primärausfällen hervorgerufen werden.

Modellierung von Redundanz

Mit der Reserveverknüpfung lässt sich eine Strategie der aktiven Fehlerbehebung durch Redundanz (z. B. bei sicherheitskritischen Systemen) modellieren.

E1 und E2 sind die Eingänge der Verknüpfung. Sie stellen redundante Funktionselemente dar: E1 für Betrieb, E2 für Reserve. Fällt E1 aus (E1: 0 → 1), so wird auf E2 durch die Umschalteinrichtung E12 (E12: 0 → 1) umgeschaltet. Nach der Reparatur kann durch die Umschalteinrichtung E21 auf die Einheit E1 zurückgeschaltet werden (E21: 0 → 1). Der Ausgang A besitzt den Wert 1, falls beide Einheiten ausgefallen sind (E1 = E2 = 1). Das System fällt somit nur dann aus, wenn auch die redundante Reserveeinheit ausgefallen ist.

Aufbau des Fehlerbaums top-down

von der Wurzel bis zu den Blättern

Die Erstellung eines Fehlerbaums für ein System erfolgt nun derart, dass komplexe Systeme top-down aus ihren Teilsystemen modelliert werden. Der Ausgang eines Teilsystems S1 wird dabei mit dem Eingang eines anderen Teilsystems S2 verknüpft, wenn der Ausfall von S1 Auswirkungen auf die Funktionsfähigkeit von S2 hat.

Eine Weiterentwicklung dieses Vorgehens ist es, anstelle von Binärwerten 0/1 die Ereignisse mit Ausfallfunktionen F(t) zu belegen, wobei Folgendes gilt:

▶Der Ausfallfunktionswert F(t1) ist die Wahrscheinlichkeit eines Ausfalls bis zur Zeit t1.

▶F(t) ist eine monoton steigende Funktion: Zum Zeitpunkt t = 0 ist die Ausfallwahrscheinlichkeit 0, für t → ∞ wird sie 1.

Sind den Eingängen einer UND-Verknüpfung die Verteilungsfunktionen F1(t) und F2(t) zugeordnet, so ergibt sich für die Ausfallfunktion des Ausgangs FA(t):

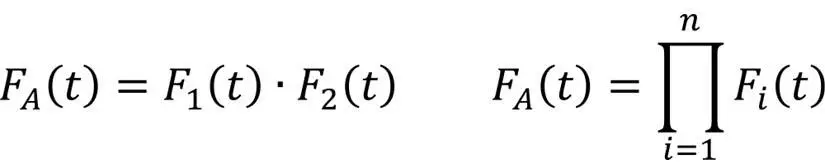
Sind den Eingängen einer ODER-Verknüpfung die Verteilungsfunktionen F1(t) und F2(t) zugeordnet, so ist die Ausfallfunktion des Ausgangs FA(t):

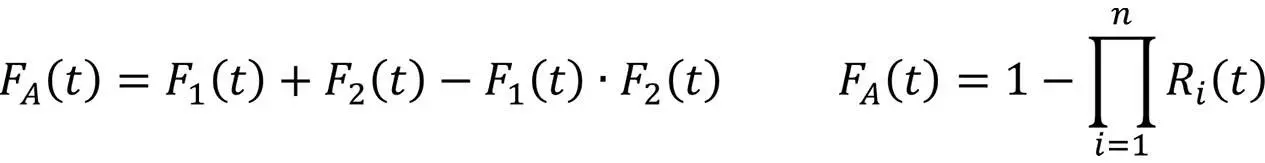
wobei die Überlebenswahrscheinlichkeit R(t) = 1 – F(t) beträgt.

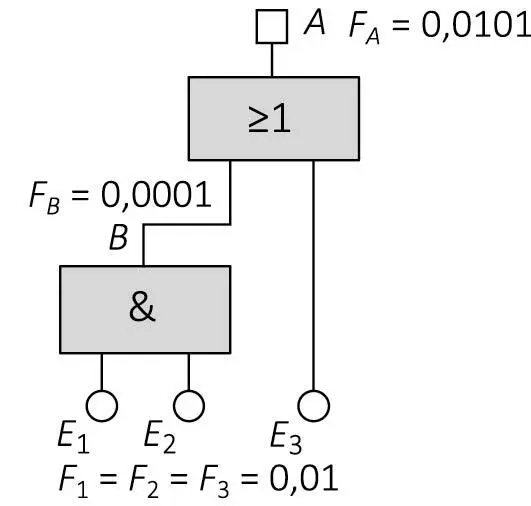
Voraussetzung für die Gültigkeit der angegebenen Formeln ist die statistische Unabhängigkeit der verknüpften Ereignisse. Ist diese gegeben, ergibt sich z. B. für die Ermittlung der resultierenden Ausfallfunktion des kleinen Beispielsystems mit den Elementarverknüpfungen UND und ODER der folgende Graph. Die quantitative Auswertung versagt allerdings, falls statistische Abhängigkeit der Ereignisse Ei vorliegt. Die Identität zweier Ereignisse (ein Ereignis tritt mehrfach auf) als Sonderfall statistischer Abhängigkeit wäre somit unzulässig. Tritt aber ein Ereignis mehrfach auf, kann ggf. der Fehlerbaum durch einfache Anwendung boolescher Algebra, in diesem Fall des Distributivgesetzes, so umgeformt werden, dass keine Ereignisredundanz mehr vorliegt (Abb. 2-2).