Anthony R. West - Solid State Chemistry and its Applications

Materials such as diamond and silicon carbide, which have very strong, directional, covalent bonds, can also be described as cp structures or eutactic structures; many have the same structures as ionic compounds. Thus, one polymorph of SiC has the wurtzite structure and it is immaterial whether Si or C is regarded as the packing atom since the net result, a 3D framework of corner‐sharing tetrahedra, is the same. Diamond can be regarded as a sphalerite structure in which half of the C atoms form a ccp array and the other half occupy T +sites, but again the two types of atom are equivalent. Classification of diamond as a eutactic structure is useful since in diamond all atoms are of the same size and it is unrealistic to distinguish between packing atoms and interstitial atoms.

Many structures have mixed ionic–covalent bonding, e.g. ZnS and CrCl 3; one advantage of describing them in terms of cp is that this can be done, if necessary, without reference to the type of bonding that is present.

Since cp structures provide an efficient means of packing atoms, many molecular compounds crystallise as cp structures even though the bonding forces between adjacent molecules are weak van der Waals forces. If the molecules are roughly spherical or become spherical because they can rotate or occupy different orientations at random, then simple hcp or ccp structures result, e.g. in crystalline H 2, CH 4and HCl. Non‐spherical molecules, especially if they are built of tetrahedra and octahedra, can also fit into a cp arrangement. For example, Al 2Br 6is a dimer with two AlBr 4tetrahedra sharing a common edge, Fig. 1.26(a). In crystalline Al 2Br 6, the Br atoms form an hcp array and Al atoms occupy one‐sixth of the available tetrahedral sites. One molecule, with the Br atoms in heavy outline is shown in Fig. 1.26(b); Al atoms occupy one pair of adjacent T +and T –sites. Br atoms 3 and 5 are common to both tetrahedra and are the bridging atoms in (a). Adjacent Al 2Br 6molecules are arranged so that each Br in the hcp array belongs to only one molecule. SnBr 4is a tetrahedral molecule and also crystallises with an hcp Br array, but only one‐eighth of the tetrahedral sites are occupied.

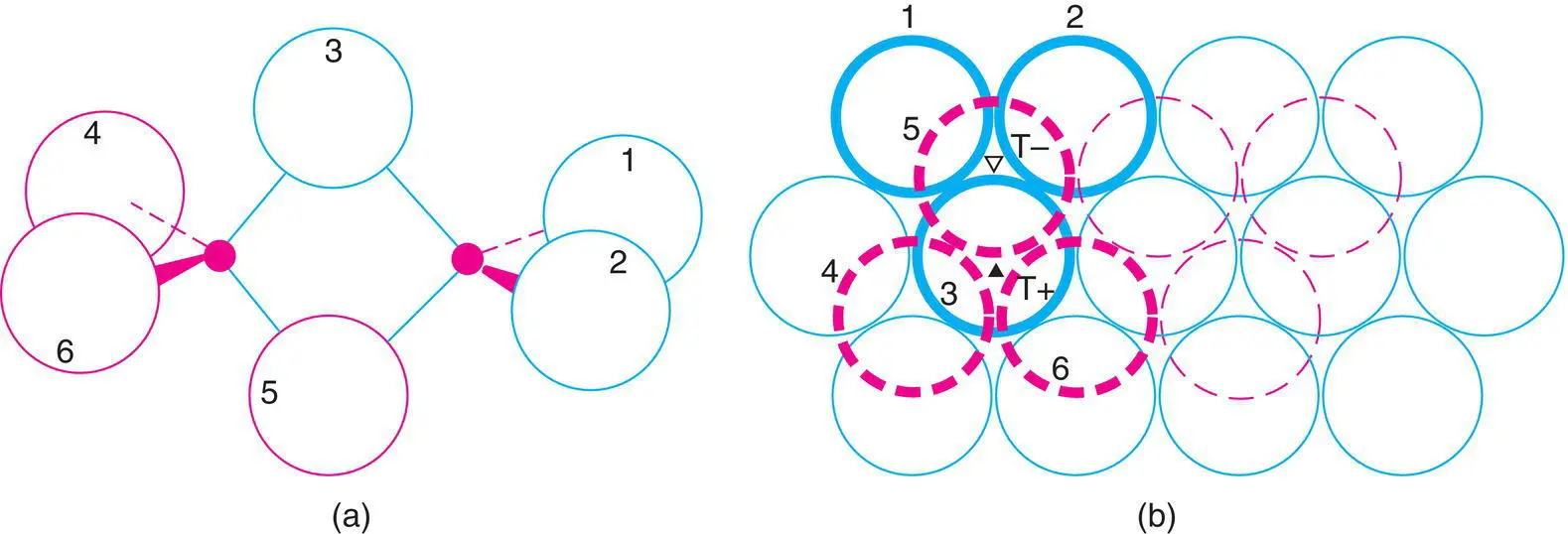
Figure 1.26 (a) hcp arrangement of Br atoms in crystalline Al2Br6; (b) Al atoms occupy T+ and T– sites. Dashed circles are below the plane of the paper.

The simplest, best known and symmetrical fullerene is C 60whose discovery led to the 1996 Nobel Prize in Chemistry awarded to Kroto, Curl and Smalley. It is a hollow, spherical cage of diameter 7.1 Å formed from 3‐coordinate (approximately sp 2hybridised) C atoms which link to form a network of 12 pentagons and 20 hexagons, Fig. 1.27(a), that match exactly the pattern on a soccer ball (hence the alternative, colloquial, American name ‘buckyball’; the name ‘fullerene’ is in honour of Buckminster Fuller, who designed the geodesic dome that has the same network structure as C 60).

Not surprisingly, in crystalline C 60, the C 60molecules arrange themselves according to the principles of close packing. At room temperature, crystalline C 60is face centred cubic, Z = 4 (C 60), a = 14.17 Å, and the C 60molecules are orientationally disordered. The separation of adjacent C 60molecules can be calculated with the aid of Fig. 1.22(a); a cube face diagonal corresponds to a cp direction from which we calculate that the centres of adjacent molecules are separated by 10.0 Å. The ‘hard diameter’ of a C 60molecule is calculated to be 7.1 Å which leaves a gap of 2.9 Å between adjacent molecules for van der Waals bonding.

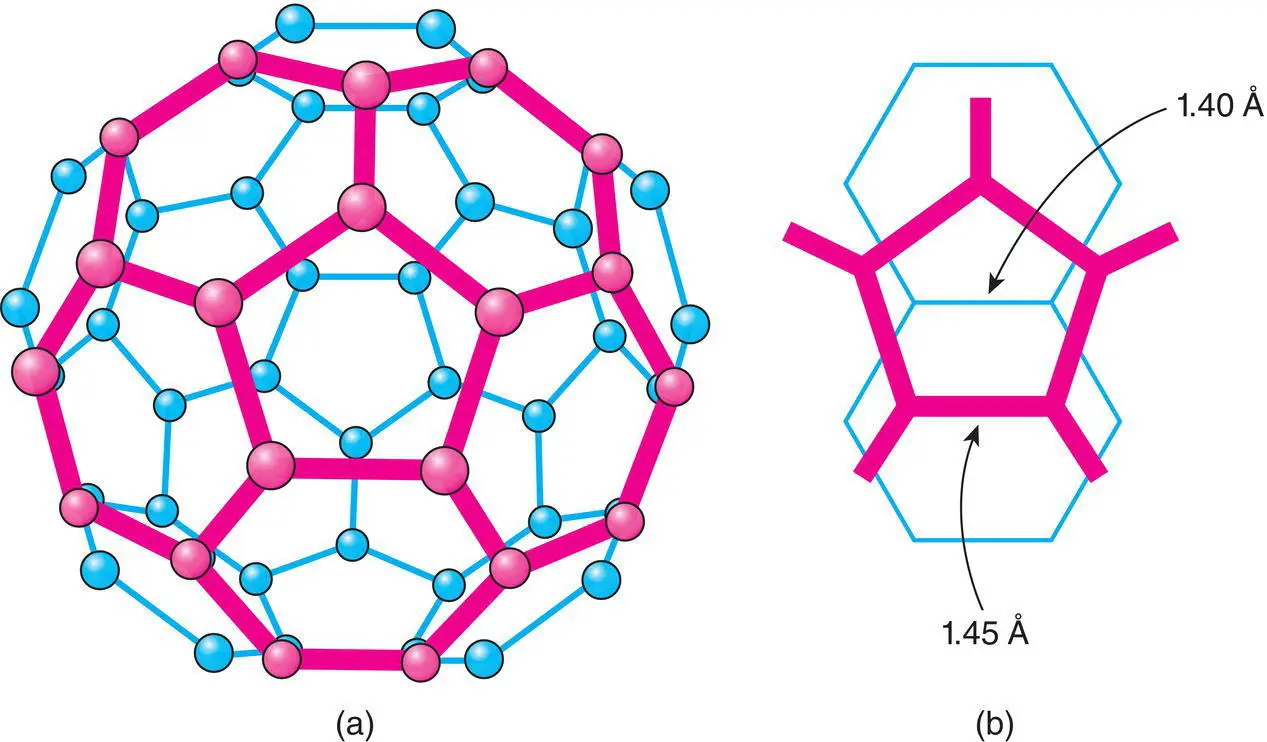
Figure 1.27 (a) The C60 molecule; one pentagon surrounded by five hexagons is shown in bold. (b) Parts of two C60 molecules in the region of closest contact showing a short C–C bond separating two hexagons in one molecule pointing towards the middle of a pentagon in an adjacent molecule.

Adapted from W. I. R. David et al., Nature 353, 147 (1991).

Because the C 60molecules are not perfectly spherical, Fig. 1.27(a), they settle into an ordered arrangement below 249 K. The driving force for this ordering is optimisation of the bonding between adjacent C 60molecules. In particular, in a given [110] cp direction, the short electron‐rich C–C bond that links two hexagons in one C 60molecule points directly at the centre of an electron‐deficient pentagon, on an adjacent C 60molecule, as shown for two ring fragments in Fig. 1.27(b).

This arrangement minimises direct C–C overlap but maximises donor–acceptor electronic interactions between adjacent molecules. The C–C bonds in fullerene fall into two groups, 1.40 Å for C–C bonds linking two hexagons and 1.45 Å for bonds linking one hexagon and one pentagon; pentagons are isolated in C 60. Comparing these with typical single and double bond lengths in organic compounds, 1.54 and 1.33 Å, respectively, we can see that the C–C bonds in C 60are of intermediate bond order.

Some other fullerenes, such as C 70, also form cp structures, even though the molecules are not spherical. Thus, the C 70molecule is an ellipsoid (shaped like a rugby ball with a long axis of 8.34 Å and a short axis of 7.66 Å), but in crystalline C 70at room temperature the ellipsoids are able to rotate freely to give quasispherical molecules on a time average which form an fcc structure, a = 15.01 Å.

cp structures have, of course, tetrahedral and octahedral interstitial sites and in C 60these may be occupied by a range of large alkali metal cations to give materials known as fullerides . The most studied C 60fullerides have general formula A 3C 60as in Rb 3C 60or K 2RbC 60, in which all T +, T –and O sites are occupied. These materials are metallic since the alkali metals ionise and donate their electrons to the conduction band of the C 60network, which is half full in A 3C 60. At low temperatures, many of these fullerides become superconducting. The highest T c(the temperature at which the metal–superconductor transition occurs on cooling, Chapter 8) to date in the fullerides is 45 K in Tl 2RbC 60.

Other fullerides exist with different patterns of occupancy of interstitial sites, e.g. rock salt or zinc blende analogues in AC 60and fluorite analogues in A 2C 60. It is also possible to increase the number of A ions per C 60beyond 3; in A 4C 60(A = Na), A 4clusters form in the octahedral sites. In A 6C 60, the packing arrangement of the C 60molecules changes from ccp to bcc ; the bcc structure has a large number of interstitial sites, e.g. twelve distorted tetrahedral sites, distributed over the cube faces in the bcc array of anions (discussed in Chapter 8, for α ‐AgI, Fig. 8.28). 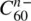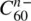This wide range of formulae arises because the C 60molecule can accept a number of electrons to give anions : n = 1, 2, 3, 4, … Part of the excitement in C 60chemistry is that the electronic properties range from insulating to metallic/superconducting, depending on the value of n .