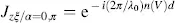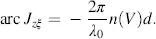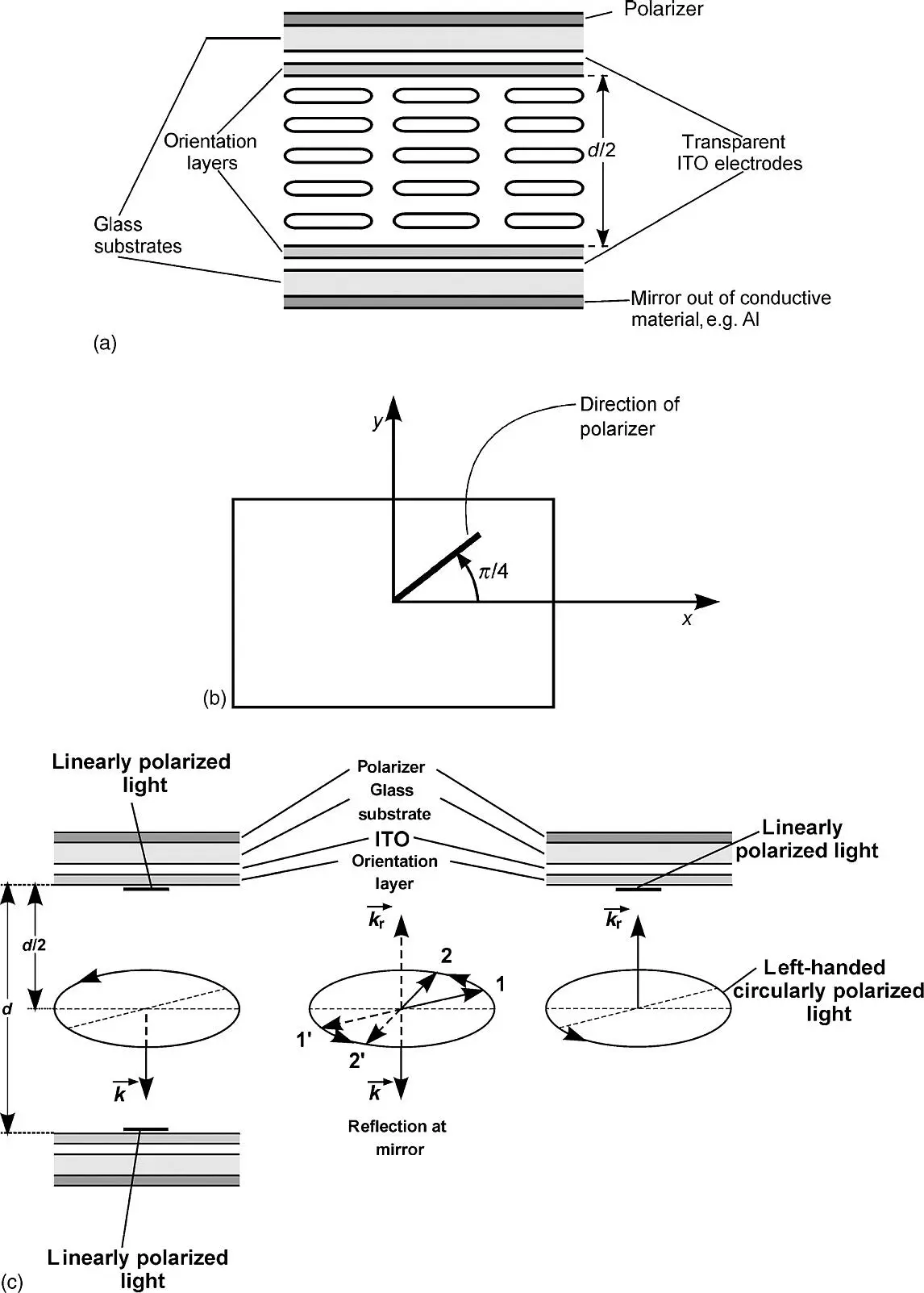
Figure 3.12 The reflective Fréedericksz cell. (a) Cross-section; (b) top view; (c) explanation of the operation of a reflective cell in the field-free state
The normally white cell with crossed polarizers cannot be transformed into a reflective version as this version has only one polarizer able to realize only parallel polarizers. This fact, however, renders the reflective cell somewhat more economic as the added mirror is cheaper than the saved polarizer.
The surface of the mirror and the lower edge of the LC material in Figure 3.12(a)are supposed to be located at z = d /2, which is not exactly feasible because of the presence of the ITO and the orientation layers. As both layers are very thin, around 100 nm each, this does not show up in the performance of the cell.
3.2.4 The Fréedericksz cell as a phase-only modulator
So far we have treated the Fréedericksz cell as an amplitude modulator, as it is required for realizing grey shades in displays. The phase was of no importance. In coherent optical signal processing, the phase of the light wave is crucial; a voltage controlled phase shift without altering the amplitude is often required. A component with that performance belongs to the group of Spatial Light Modulators (SLMs). Another SLM is a pixellated optical multiplier in the form of an LCD placed behind a picture in Figure 3.13. Each area in front of the pixels of the multiplier is multiplied by the grey shade in those pixels. In other words, it is multiplied by a value 1 corresponding to a fully transparent pixel, a value 0 corresponding to a black pixel, and all values ε(0, 1) corresponding to the grey shades. As this multiplication occurs with the speed of light and with all pixels operating in parallel, extremely high processing speeds are feasible with the SLMs of an electro-optical processor (Lu and Saleh, 1990).
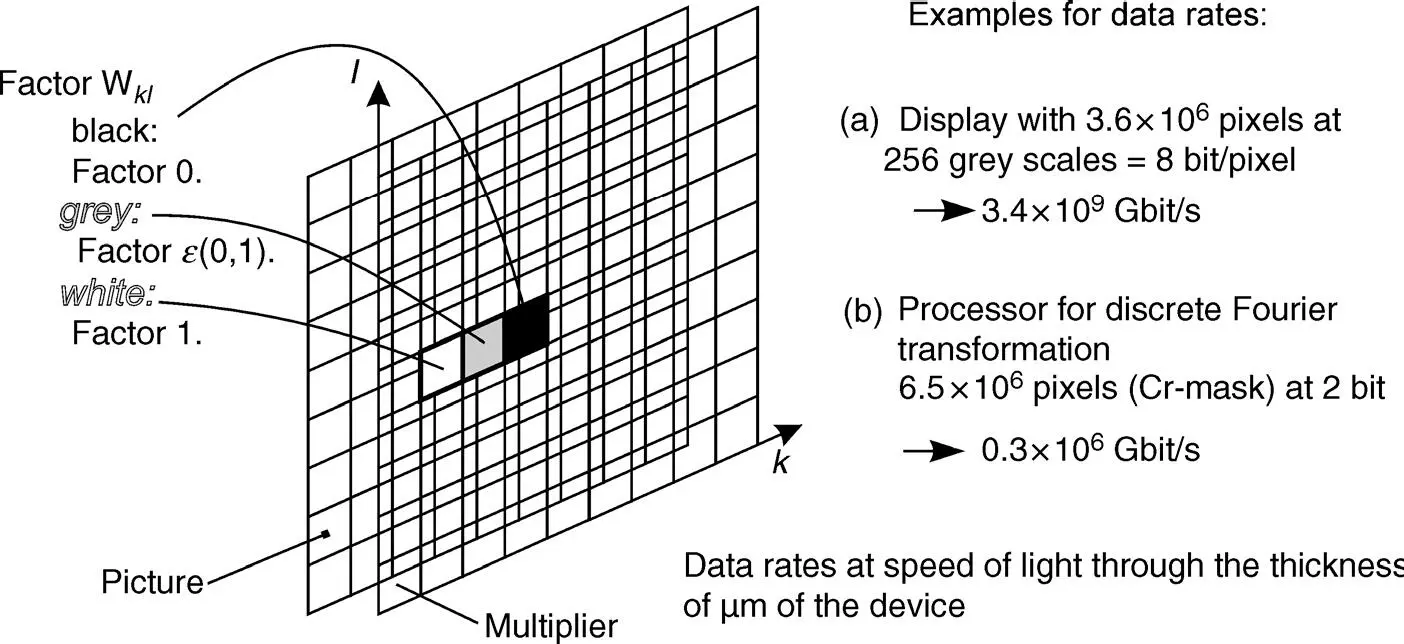
Figure 3.13 An LCD used as an SLM operating as a multiplier
The explanation of the SLM for phase-shifts starts with the most general Equations (3.40)and (3.41)of the Freedericksz cell containing the arbitrary angle a of the polarizer at the input and the pertinent angle γ of the analyser ( Figures 3.4(a)and 3.8).
Equations (3.40)and (3.41)yield, for γ = α (that is, for parallel polarizers), the Jones vectors Jzξ and Jzη measured in the ξ−η coordinates in Figure 3.4(a)
(3.88) 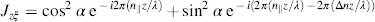
(3.89) 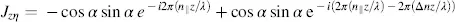
The Jones vector Jz% of the light passing through the analyser parallel to the polarizer is, for a = 0, n and a = n/2 and for no voltage applied,
(3.90) 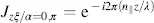
and
(3.91) 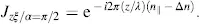
The magnitude is constant, whereas the phase changes with the distance z from the input.
| Jzξ | from Equation (3.88)is plotted in Figure 3.14versus α and z . The constant magnitude 1 for α = 0, (π/2) and π independent of z is visible as well as the maximum amplitude modulation for α = π/4. However, we want arc Jzξ to change with the voltage V across the cell. To this aim, we consider the Fréedericksz cell in Figure 3.15, where a voltage has been applied to tilt the molecules by an angle φ . The linearly polarized light E 0stemming from the polarizer with angle α = 0 to the x -axis has to meet the boundary condition at the transition from the polarizer into the cell. The tangential components have to be equal on both sides, which means they are E 0in Figure 3.15. This indicates that the light wave has the wave vector 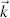 parallel to the z -axis. If no voltage V is applied, the LC molecules are parallel to the surface and the x -axis, yielding
parallel to the z -axis. If no voltage V is applied, the LC molecules are parallel to the surface and the x -axis, yielding
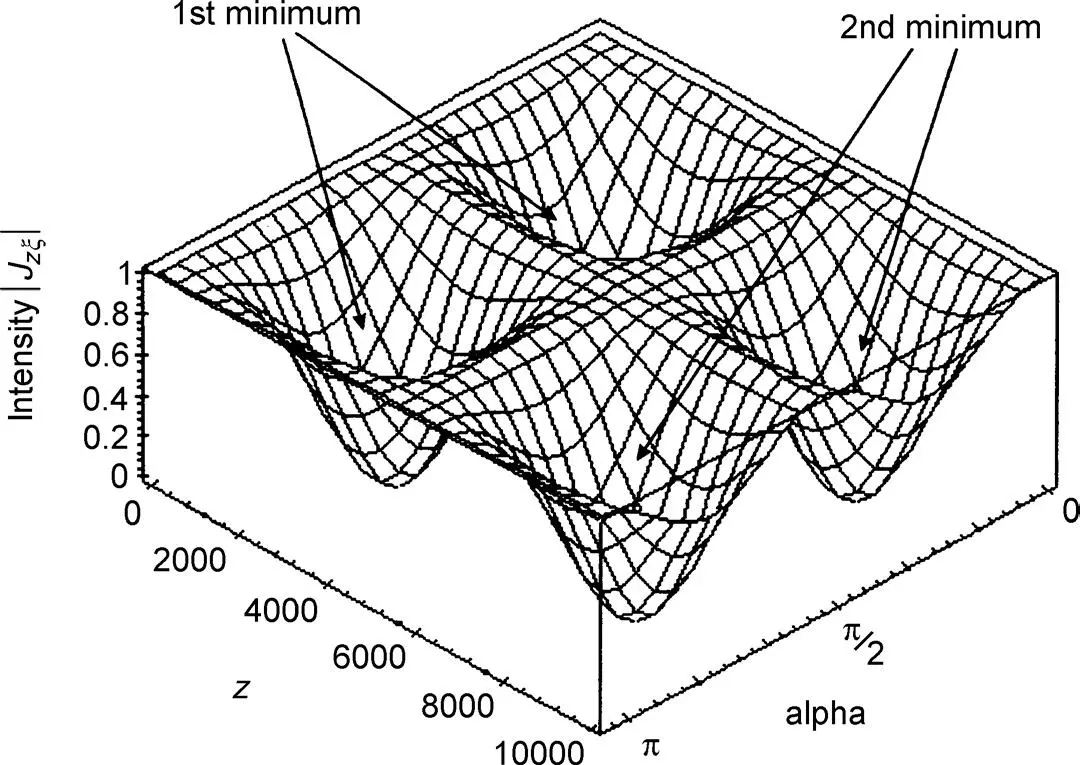
Figure 3.14 | Jzξ | in Equation (3.88)plotted versus α and z
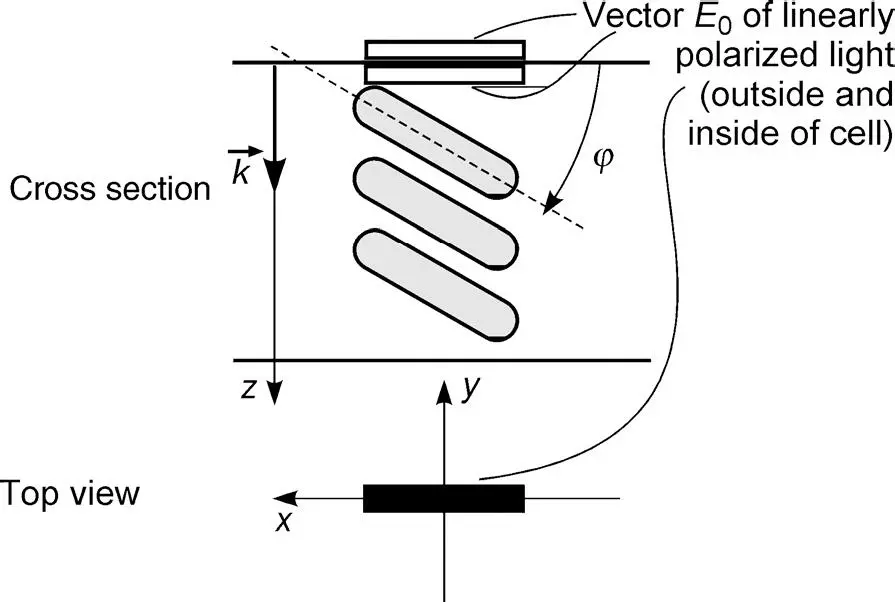
Figure 3.15 The linearly polarized light in parallel (α = 0) to the projection of the long axis of the LC molecules into the x-y plane
(3.92) 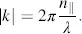
With a large enough voltage V , all molecules are perpendicular to the surface or the x -axis, yielding
(3.93) 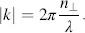
From Equations (3.92)and (3.93), we detect the voltage-induced change of the refraction index 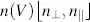 with n ||for the lower voltage and n┴ for the higher voltage. Along with Equation (3.90), for a given wavelength λ 0and for z = d , this provides
with n ||for the lower voltage and n┴ for the higher voltage. Along with Equation (3.90), for a given wavelength λ 0and for z = d , this provides
(3.94) 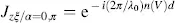
with
(3.95) 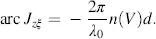
How n changes with V cannot yet be determined. For that we need the propagation of light obliquely to the LC molecules, which will be discussed in Chapter 6. So far, arc Jzξ ( V ) is determined by measurements.
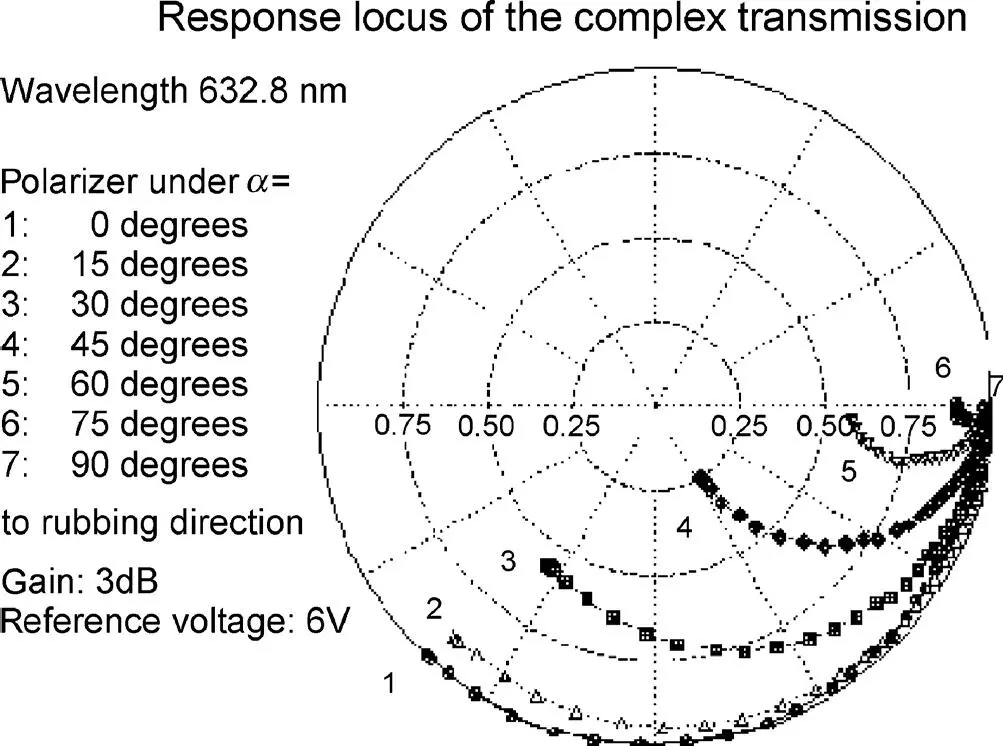
Figure 3.16 Measured phase-shift curves of a Fréedericksz cell
For λ 0= 0.5 μ, n┴ = 14 and n ||= 1.5 we notice that arc Jzξ may change from 2.8 × 2π × d to 3.2π × d . Obviously, the larger d the larger is the change of arc Jzξ , however, the necessary addressing voltage increases. For d = 3 μ we obtain arc Jzξ= [8.4 × 2π, 9 × 2π], a change of 0.6 × 2π. Figure 3.16shows in curve 1 with a = 0 a phase-only SLM with a maximum phase shift of 0.75π. Due to Equation (3.88), the other curves with a ≠ 0 cannot possess a constant magnitude, as is also visible in Figure 3.14.
Читать дальше



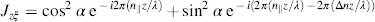
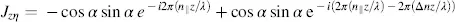
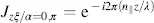
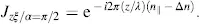
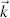 parallel to the z -axis. If no voltage V is applied, the LC molecules are parallel to the surface and the x -axis, yielding
parallel to the z -axis. If no voltage V is applied, the LC molecules are parallel to the surface and the x -axis, yielding

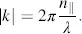
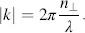
 with n ||for the lower voltage and n┴ for the higher voltage. Along with Equation (3.90), for a given wavelength λ 0and for z = d , this provides
with n ||for the lower voltage and n┴ for the higher voltage. Along with Equation (3.90), for a given wavelength λ 0and for z = d , this provides