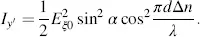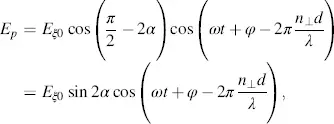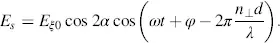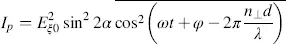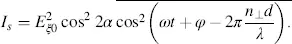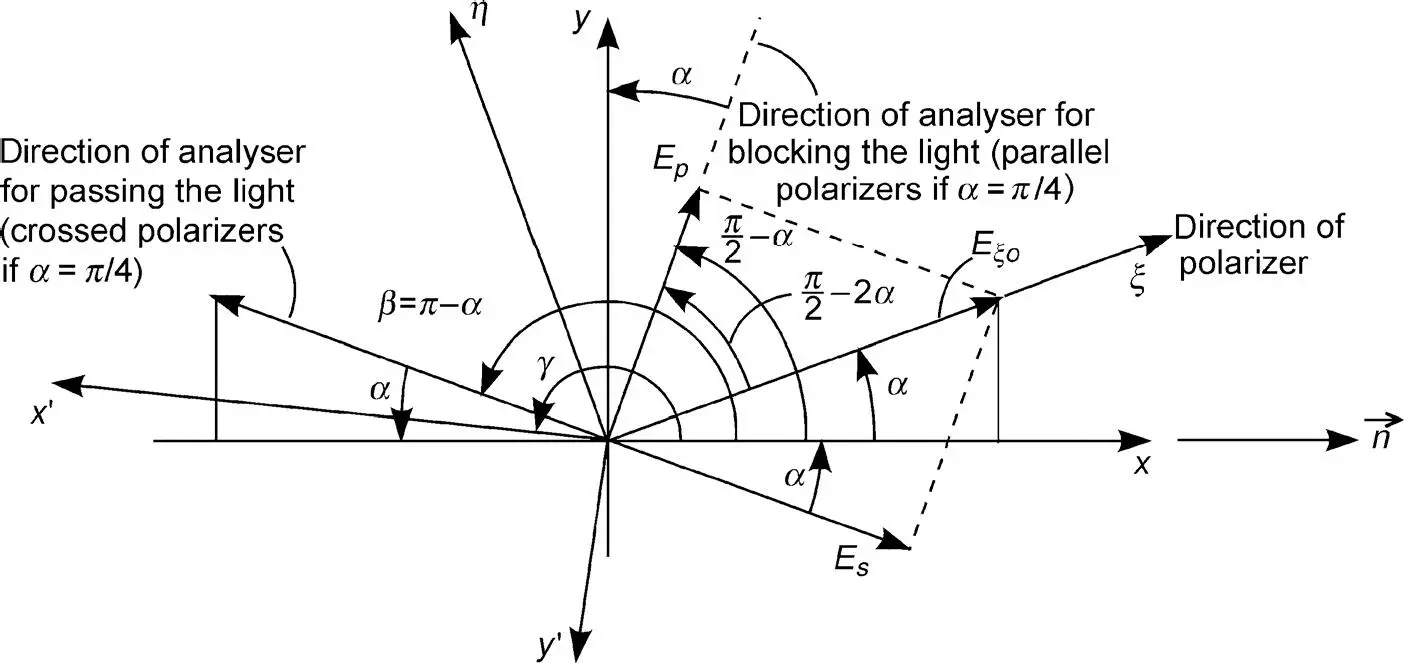
Figure 3.8 Angles of polarizer and analyser for the Fréedericksz cell
At the output of the cell for z = d , where d is the thickness of the cell, the retardation is
(3.57) 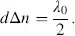
This retardation is associated with a change of phase by δ = π after the wave has propagated the distance d through the cell. The cell operates as a λ /2-plate. Obviously, the retardation is the phase shift measured in parts of λ 0.
For linear polarization with wavelength λ 0corresponding to the angular frequency ω 0of the electric field, the components in Equations (3.42)and (3.43)at z = d are
(3.58) 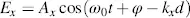
(3.59) 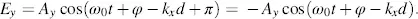
Equations (3.58)and (3.59)reveal the angle β of the linearly polarized light at z = d as
(3.60) 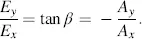
Due to Equations (3.46)and (3.47), we obtain on the other hand for the light at z = 0
(3.61) 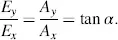
Equations (3.60)and (3.61)indicate
(3.62) 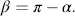
as shown in Figure 3.8, where all important angles for a Fréedericksz cell are drawn.
The result for a wavelength λ 0at the output z = d of a cell without a voltage applied is linearly polarized light at an angle β = π − а , where α is the angle of the incoming linearly polarized light. If we place the analyser in the direction β = π − α the light can pass representing the normally white mode. The analyser perpendicular to β that is at an angle π/2 − α in Figure 3.8blocks the light representing the normally black mode. We will investigate these two modes in greater detail.
We choose the angle γ for which the x′−y′ plane in Figure 3.8is rotated from the x−y plane as γ = β = π − α. This provides, along with Equations (3.40)and (3.41),
(3.63) 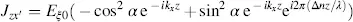
(3.64) 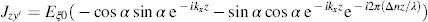
or for the electrical field
(3.65) 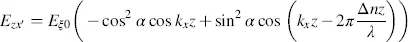
and
(3.66) 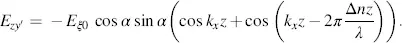
For the wavelength λ = λ 0in Equation (3.57), we obtain at z = d
(3.67) 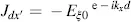
(3.68) 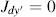
as expected, since we know already that at z = d light with wavelength λ 0is linearly polarized in the direction β = π − α. For this case, the Jones vectors provide the components of the electrical field as
(3.69) 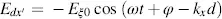
(3.70) 
Now we place the analyser perpendicular to the angle β = π − α that is in the direction with angle γ = π /2 − α in Figure 3.8. For this case Jzx ′is identical to − Jzy ′in Equation (3.64)and (3.66)and Jzy ′is identical with Jzx ′in Equations (3.63)and (3.64). Hence, we investigate Equations (3.63)through (3.66)for both cases. The intensity I′x = |Jdx ′ | 2for z = d is, with Equation (3.63),
(3.71) 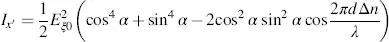
or
(3.72) 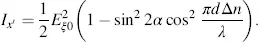
For 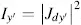 , Equation (3.64)yields
, Equation (3.64)yields
(3.73) 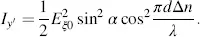
In order to learn how to choose a , we now consider the case of a large enough voltage across the LC cell to fully orient the LC molecules apart from two thin layers on top of the orientation layer, due to Δ ε > 0 in parallel to the electric field. The linearly polarized light coming in at angle a no longer experiences birefringence, as it is only exposed to the refractive index n┴ . It reaches the plane z = d with the phase shift 2π( n┴d / λ ). Its component Ep passing an analyser with the angle (π/2) − α in Figure 3.8is
(3.74) 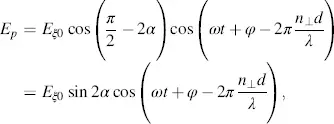
whereas the component Es passing an analyser with the angle π − α in Figure 3.8is
(3.75) 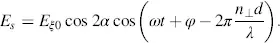
The intensities belonging to Ep and Es are
(3.76) 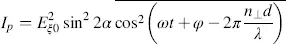
and
(3.77) 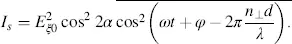
The bar over the cos terms means the average over time needed for calculating the intensity. The maximum of Ip occurs for α = π/4, which (according to Figure 3.8) places the polarizer and analyser in parallel. Is assumes a maximum for α = 0, for which again the polarizer and analyser pertaining to Es are in parallel.
Читать дальше


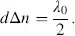
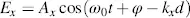
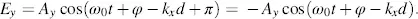
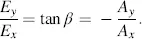
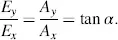
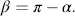
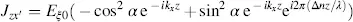
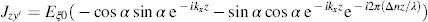
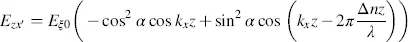
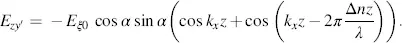
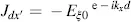
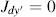
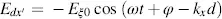

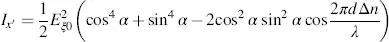
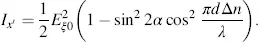
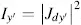 , Equation (3.64)yields
, Equation (3.64)yields