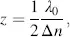From Equations (3.35)and (3.32), we derive the scalars according to Equation (3.10)for the components Ex and Ey in the distance z
(3.42) 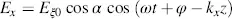
and
(3.43) 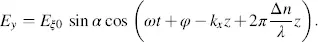
Equations (3.42)and (3.43)represent the electric field in the x−y coordinates after having travelled the distance z through the Fréedericksz cell, whereas Equations (3.40)and (3.41)give the Jones vectors in the x′−y ′ coordinates at distance z . These equations will be evaluated with respect to the amplitude modulation in the next two chapters, and the phase modulation in Section 3.2.4. In the remaining portion of this chapter, we investigate the polarization of the light while it travels through the Fréedericksz cell.
We start with Equations (3.42)and (3.43), and calculate the locus of the vector 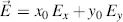 in the x−y plane as time evolves. To this aim, we eliminate τ = ωt + φ and, after some algebraic steps presented in Appendix 3, reach the result (Born and Wolf, 1980)
in the x−y plane as time evolves. To this aim, we eliminate τ = ωt + φ and, after some algebraic steps presented in Appendix 3, reach the result (Born and Wolf, 1980)
(3.44) 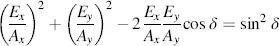
where
(3.45) 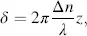
(3.46) 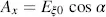
and
(3.47) 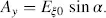
This is a conic. From Equations (3.42)and (3.43), it can be seen that the conic must lie within the rectangular region bordered by the lines x = ±Ax and y = ±A y, as shown in Figure 3.5. Hence, the conic is an ellipse and light is called elliptically polarized. Equation (3.44)indicates that the principal axes of the ellipse are not parallel to the x - and y -axes; they are parallel to the ξ- and η- axes in Figure 3.5, in which the equation for the ellipse is
(3.48) 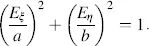
The principal axes a and b are given by
(3.49) 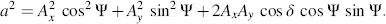
(3.50) 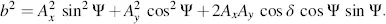
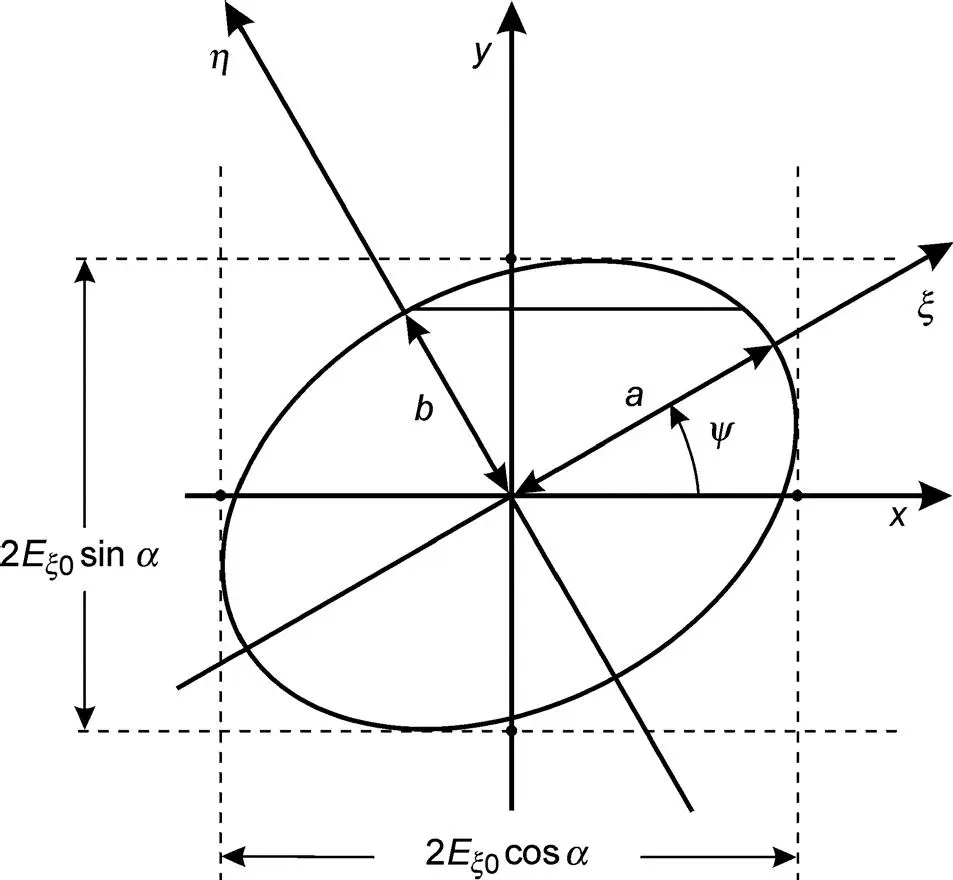
Figure 3.5 The ellipse as locus for the vector of the electric field
The angle Ψ for the rotation is determined by
(3.51) 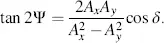
A derivation for Equations (3.48)through (3.51)can be found in Born and Wolf (1980), and is repeated in Appendix 3.
The sense of revolution of the E -vector with increasing time is determined by Equations (3.42)and (3.43). If Ey is time-wise ahead of Ex, this happens for 0< δ < π, i.e., for sin δ > 0 with δ in Equation (3.45), then the rotation of E is right-handed elliptically polarized, as shown in Figure 3.6; if Ey lags Ex, that happens for π < δ < 2π or sin δ < 0, the rotation is left-handed elliptically polarized (see Figure 3.6). The polarization dependent upon δ is depicted in Figure 3.7. The sense of revolution may be verified by plotting Ex and Ey with increasing time until the change of one of these components alters its sign.
Two special cases are the linear and the circular polarization. For
(3.52) 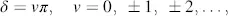
Equation (3.44)degenerates into
(3.53) 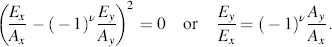
Ex and Ey lie on a straight line in Figure 3.7. This is the case of linearly polarized light. For Ax=Ay and
(3.54) 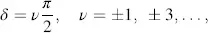
Equation (3.44)provides the circle
(3.55) 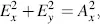
which represents circularly polarized light as also depicted in Figure 3.7.
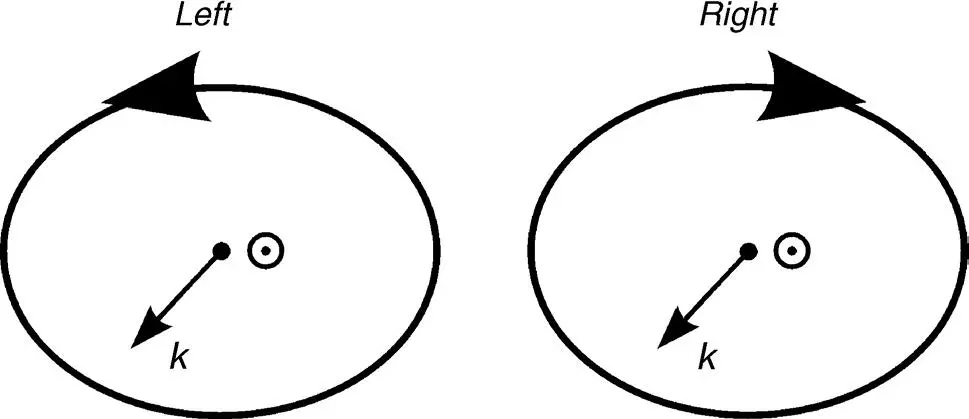
Figure 3.6 Right- and left-handed elliptically polarized light seen against the propagating wave with wave vector k .  viewing against the arrow of k
viewing against the arrow of k
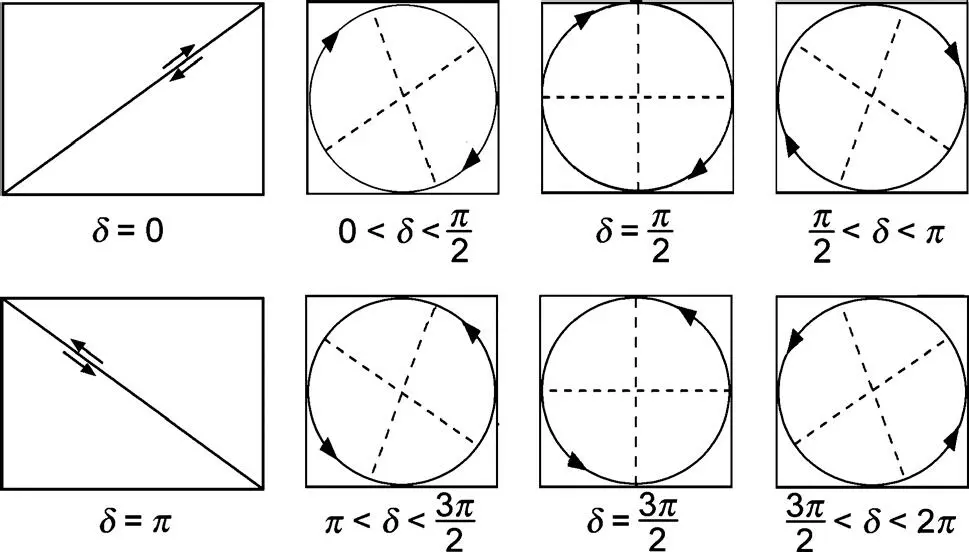
Figure 3.7 Elliptical, circular and linear polarization for different phase differences δ = 2π(Δ n / λ )z (Reproduced from Born and Wolf, 1980 with permission of Elsevier.)
Further characterizations of the polarization are given in Chapter 5. We are now ready to evaluate the results obtained so far for the Fréedericksz cell.
3.2.2 The transmissive Fréedericksz cell
In Figure 3.8we continue the discussion of the transmissive cell begun with Figures 3.4(a)and 3.4(b). The incoming linearly polarized light enters at an angle α in Figure 3.8. The linear polarization occurs again according to Equation (3.52)at δ = 2π(Δ n / λ ) z = vπ, v = ±1, ±2, ..or for v = 1 at the smallest z -value
(3.56) 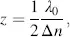
where λ 0is the pertinent wavelength.
Читать дальше

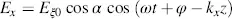
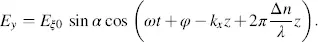
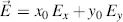 in the x−y plane as time evolves. To this aim, we eliminate τ = ωt + φ and, after some algebraic steps presented in Appendix 3, reach the result (Born and Wolf, 1980)
in the x−y plane as time evolves. To this aim, we eliminate τ = ωt + φ and, after some algebraic steps presented in Appendix 3, reach the result (Born and Wolf, 1980)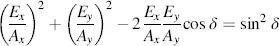
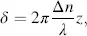
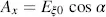
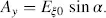
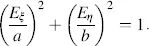
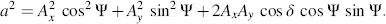
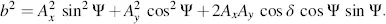

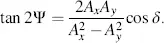
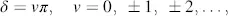
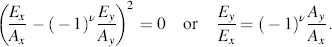
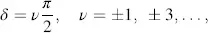
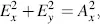

 viewing against the arrow of k
viewing against the arrow of k