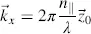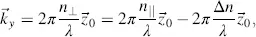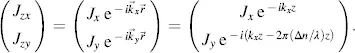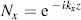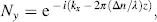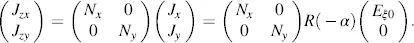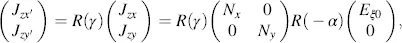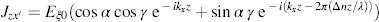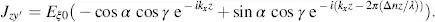In a physical sense, J is not a vector as so far it consists only of two components and the vector product does not apply. It can also be termed a Jones matrix. According to Equation (3.10), the scalars associated with the Jones vector are
(3.24) 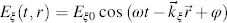
and
(3.25) 
In later investigations, the rectangular coordinates ξ and η will have to be rotated by an angle a into the new rectangular coordinates x and y, as shown in Figure 3.3. The vector E with the components E ξand Eη is transformed into the components Ex and Ey in the x - y -plane according to
(3.26) 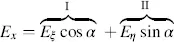
(3.27) 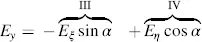
if rotation by a is positive in the counter-clockwise direction. The roman numerals in Equations (3.26)and (3.27)indicate the sections marked in Figure 3.3, thus providing Equations (3.26)and (3.27). The matrix equation for (3.26)and (3.27)is
(3.28) 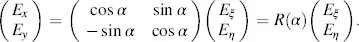
R (α) is the rotation matrix, and R(−α ) stands for a rotation in clockwise direction.
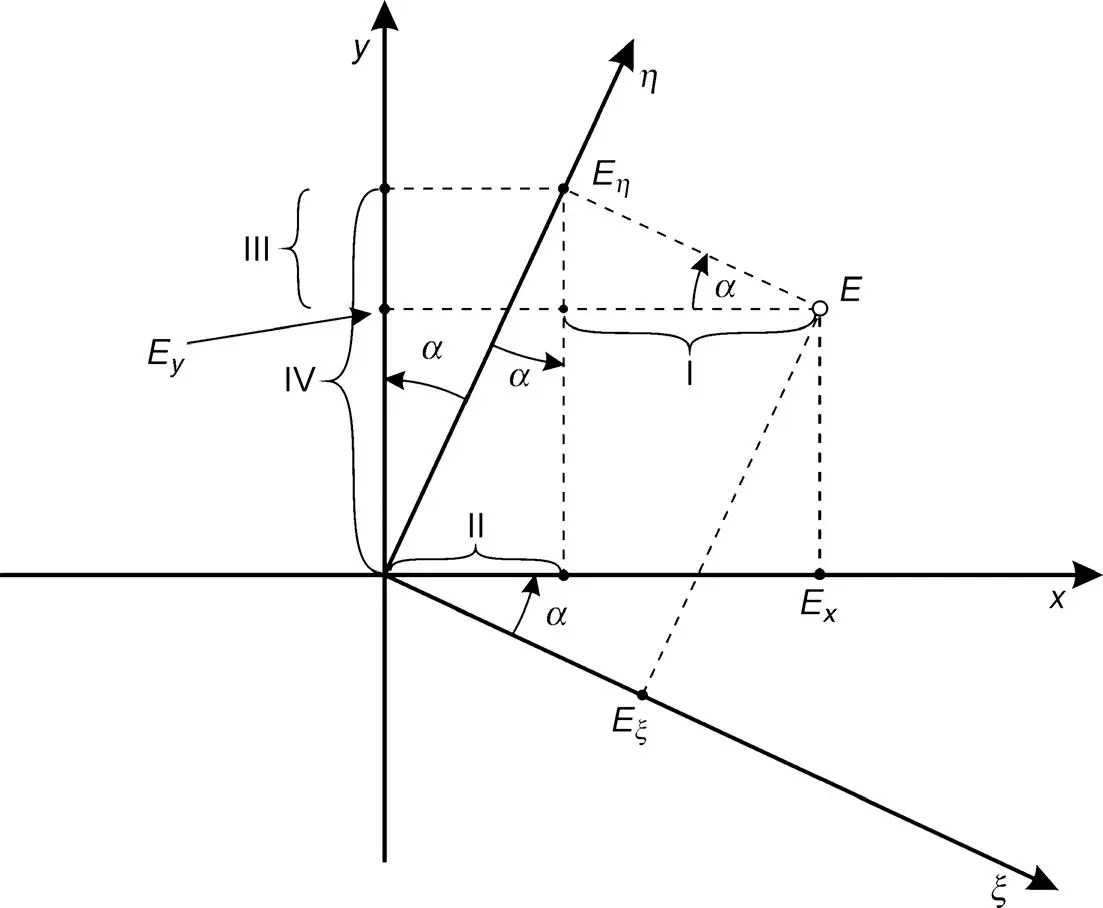
Figure 3.3 Rotation of the ξ − η coordinates by a into the x-y coordinates
3.2 Propagation of Polarized Light in Birefringent Untwisted Nematic Liquid Crystal Cells
3.2.1 The propagation of light in a Fréedericksz cell
We investigate the liquid crystal cell according to Fréedericksz (Fréedericksz and Zolina, 1933; Yeh and Gu, 1999) with the top view in Figure 3.4(a)and the cross-section perpendicular to the top plane A in Figure 3.4(b). The vector E of the electric field in the plane A defined in the cartesian ξ − η- coordinates has the components using the notations in Equation (3.12)
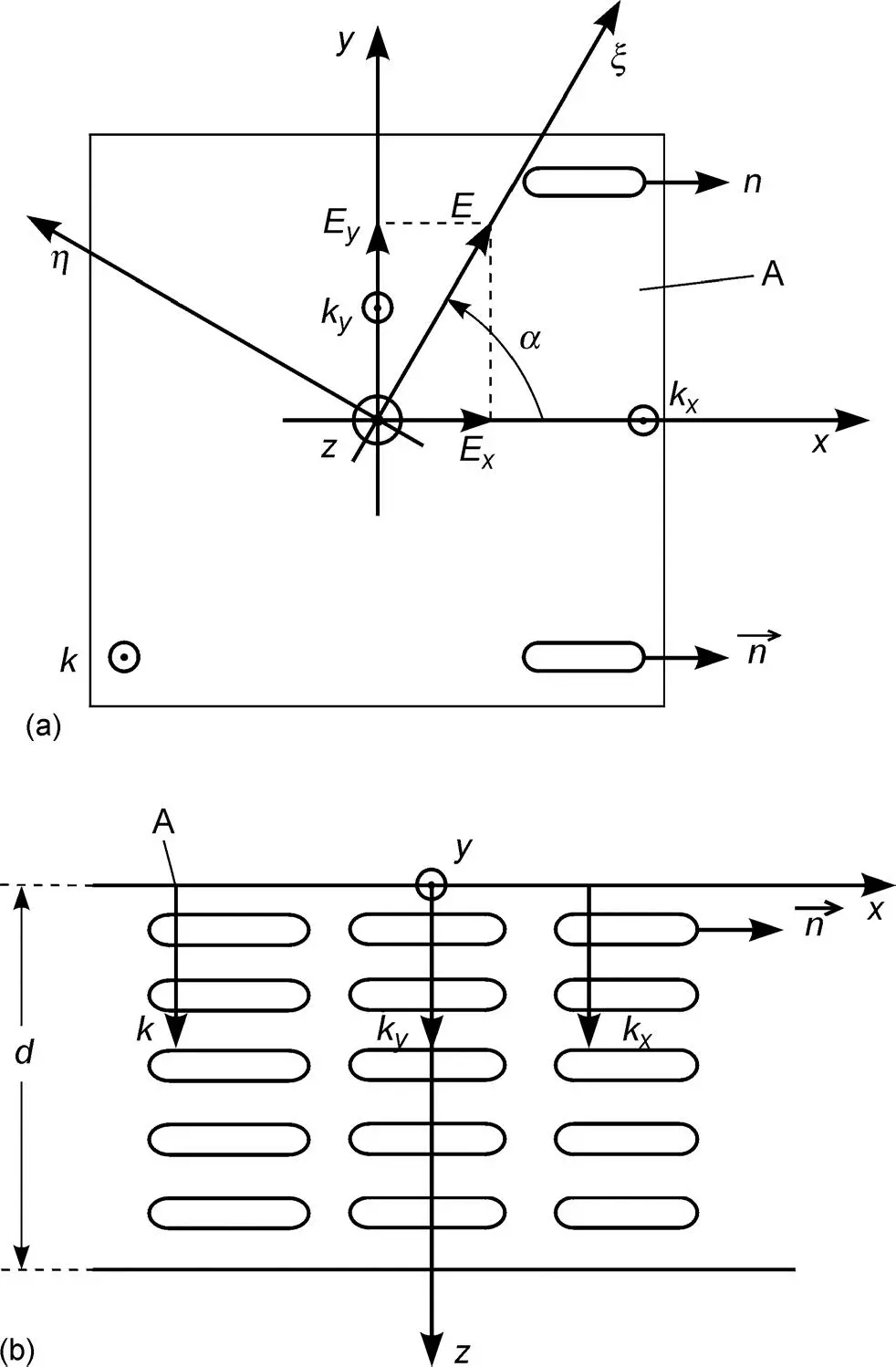
Figure 3.4 (a) Top view of Fréedericksz cell with direction of LC molecules and vector E of electric field; (b) cross section of LC cell with parallel layers of molecules and wave vectors k, kx and ky
(3.29) 
and
(3.30) 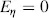
with the Jones vector introduced in Equation (3.23)
(3.31) 
J represents a plane harmonic wave entering the cell at z = 0 with wave vector k in Figure 3.4(b)perpendicular to A . The electric field E oscillates for all times t in a straight line; this is called a linearly polarized wave.
To obtain the components Jx and Jy of the Jones vector parallel and perpendicular to the director n of the parallel aligned LC molecules in the cell with thickness d in Figure 3.4(b), we rotate the ξ − η coordinates clockwise into the x−y plane according to Equation (3.28), which provides
(3.32) 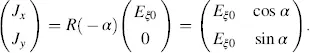
While propagating through the cell, the component Jx parallel to  experiences the refractive index n ||and the wave vector kx perpendicular to A or parallel to the unit vector z 0in Figure 3.4(b), whereas Jy sees the refractive index n┴ and the wave vector ky parallel to z 0. The wave vectors are
experiences the refractive index n ||and the wave vector kx perpendicular to A or parallel to the unit vector z 0in Figure 3.4(b), whereas Jy sees the refractive index n┴ and the wave vector ky parallel to z 0. The wave vectors are
(3.33) 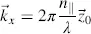
and
(3.34) 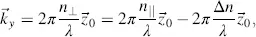
where Equation (2.5)has been used.
The Jones vector in the plane in the distance r = z × z 0from the top plane in Figure 3.4(a)is
(3.35) 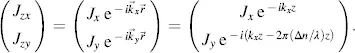
With
(3.36) 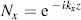
and
(3.37) 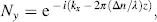
we obtain the matrix equation by also inserting Jx and Jy from Equation (3.32):
(3.38) 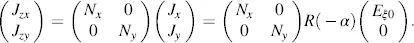
The evaluation of the result of Equation (3.38)in the x′ − y′ coordinates rotated from the x−y plane by the angle γ requires the components Jzx′ and Jzy′ , given as
(3.39) 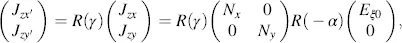
leading with Equations (3.36)and (3.37)to
(3.40) 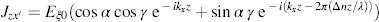
and
(3.41) 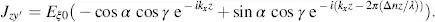
Читать дальше

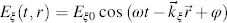

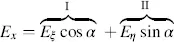
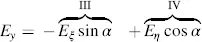
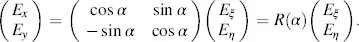



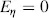

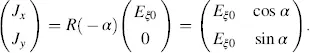
 experiences the refractive index n ||and the wave vector kx perpendicular to A or parallel to the unit vector z 0in Figure 3.4(b), whereas Jy sees the refractive index n┴ and the wave vector ky parallel to z 0. The wave vectors are
experiences the refractive index n ||and the wave vector kx perpendicular to A or parallel to the unit vector z 0in Figure 3.4(b), whereas Jy sees the refractive index n┴ and the wave vector ky parallel to z 0. The wave vectors are