Ernst Lueder - Liquid Crystal Displays

In Figures 3.9and 3.10, the intensities Iy′ and Ix′ in Equations (3.73)and (3.72)are plotted versus x= (π d Δ n /λ) and λ = (πd Δ n / x ). Iy′ in Figure 3.9becomes zero at

(3.78)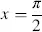

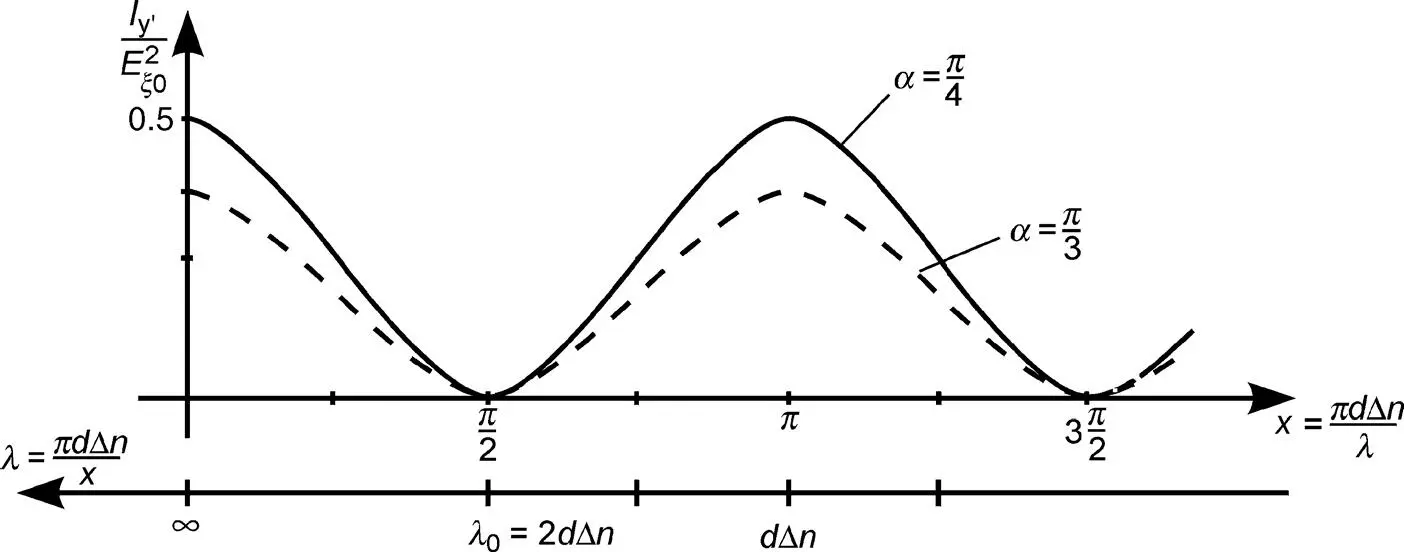
Figure 3.9 The intensity Iy , of the Fréedericksz cell for two values of α in Equation (3.73)

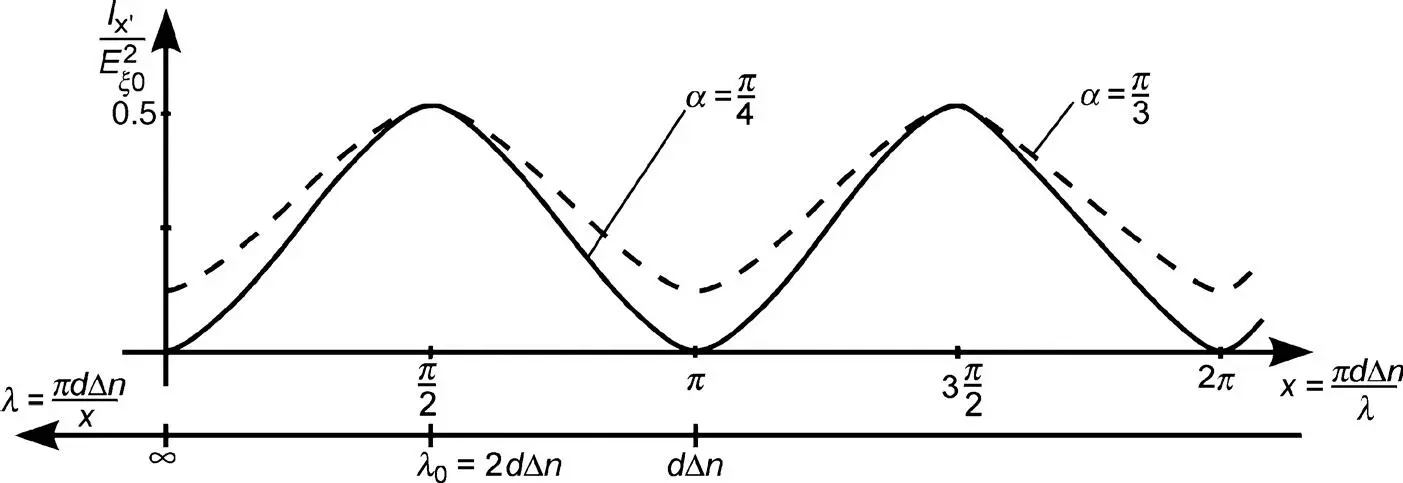
Figure 3.10 The intensity Ix , of the Fréedericksz cell for two values of α in Equation (3.72)

or

(3.79)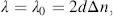

from which

(3.80)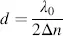

follows. The function cos 2 x is lowered around x = π /2 by the multiplication with sin 22 α . This is most welcome, as it enhances the black state, which is imperfect by the suppression of only λ 0 . This is demonstrated by two values for a in Figure 3.9. The intensity Ix′ in Equation (3.72)exhibits the same dependence on x as Iy′ , and is plotted in Figure 3.10, demonstrating that at x = π/2

(3.81)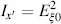

is the maximum intensity independent of α , which passes an analyser placed in the direction x′ .

We are now ready to determine the contrast C ( α ) for the normally black and normally white cell as a function of α . C is defined as

(3.82)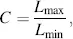

where L maxis the maximum luminance assumed to be proportional to the maximum intensity, whereas L minstands for the minimum luminance assumed to be proportional to the minimum intensity.

We first investigate the normally white mode. In the field-free state, the incoming linearly polarized light with angle α in Figure 3.11(a)again generates linear polarization for a wavelength λ 0at the angle β = π − α in Equation (3.62)with the intensity Ix′ given in Equation (3.72)representing the white state. If a large enough field is applied, the light reaches the analyser linearly polarized in the direction α independent of λ . Hence, the analyser in Figure 3.11(a)allows the component

(3.83)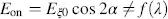

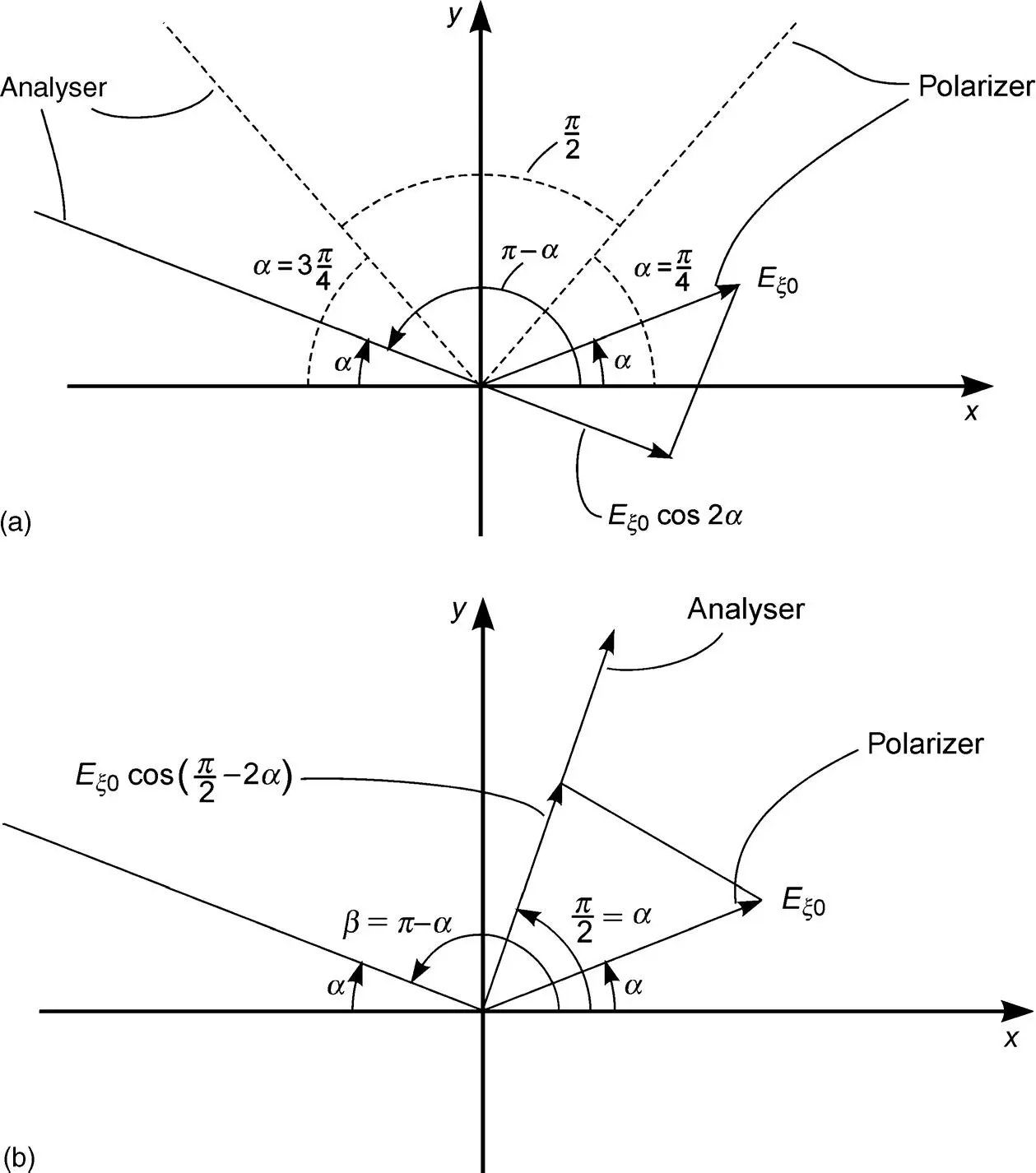
Figure 3.11 The angles of the electric field and the polarizers in a normally white Fréedericksz cell with linearly polarized light at the output d = λ/ 2Δ n . (a) Crossed polarizers; (b) parallel polarizers

to pass. This represents the black state. From Equations (3.72)and (3.83), we obtain the contrast in Equation (3.82)as

(3.84)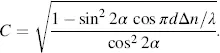

The optimum contrast is reached for a = π/4 for which C → ∞ because the denominator in Equation (3.84)is zero for all wavelengths. Further, for a = π/4 the numerator is maximum. The case a = π/4 is shown with dotted lines in Figure 3.11(a). The analyser is perpendicular to the linear polarized light at the output if a field is applied, and hence provides blocking of light independent of λ .

The normally black mode is shown in Figure 3.11(b). The analyser is perpendicular to the angle β = π − α, and allows the intensity Iy′ in Equation (3.73)to pass. This represents the black state. If a large enough field is applied, the light with the electrical field

(3.85)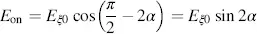

independent of wavelength can pass the analyser according to Figure 3.11(b). This is the white state. The contrast is with Equations (3.85)and (3.73)

(3.86)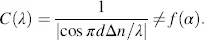

For the single wavelength λ 0in Equation (3.79), C is infinite as λ 0is blocked; this does not apply for other wavelengths in the light. Therefore, contrast in the normally black state is inferior to the contrast in the normally white state in Equation (3.84). An optimum C dependent on α does not exist. For α = π/4 the normally black cell has two parallel polarizers. This configuration will be used for reflective cells.

A reflective cell is depicted in Figure 3.12(a)(Uchida, 1999; Lueder et al. , 1998). The polarizer transmits linearly polarized light again at an angle of π/4 to the x -axis in Figure 3.12(b). The illumination is provided either by ambient light or by an external light source above the polarizer. After having travelled through the cell in Figure 3.12(a)with half the thickness d /2 of a transmissive cell, the light is reflected at the mirror usually made of Al and finally exits through the same polarizer. Thus, the reflective cell saves one polarizer. The reflective cell can be designed according to the general principles, which will be outlined now (Lueder et al. , 1998). We first recall the operation of a Freedericksz cell with parallel polarizers as depicted in the left column of Figure 3.12(c). We know that linearly polarized incoming light in the direction α = π/4 to the x -axis is blocked at z = d for wavelength λ 0. Due to Equation (3.80), the thickness is d = λ 0/2Δ n . We determine at which value z the light is circularly polarized.

With Equation (3.45)this happens for the first time for δ = π/2, reflecting in

(3.87)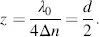

As sin δ = sin(π/2) > 0 the light is right-handed circularly polarized seen against 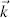, as indicated in the middle column of Figure 3.12(c). The highly conductive mirror in the middle column in Figure 3.12(c)reflects this light which is drawn with solid lines in two positions from 1 to 2 for increasing time. Since the mirror cannot sustain an electric field as the high conductance shortens the fields, the field vectors 1 and 2 have to be compensated by vectors 1′ and 2′ of the reflected light shown with dashed lines. The reflected light propagates in the direction of the wave vector 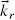, and it represents left-handed circularly polarized light seen against kr. The upwards travelling reflected light in the right column in Figure 3.12(c)images the downward moving light in the left column, and is blocked in the polarizer as linearly polarized light, in the same way as the downward travelling light is at its lower polarizer. The described imaging of the downward wave by the reflected wave can no longer take place if the mirror is not placed at z = d/ 2. Therefore, many reflective cells are constructed according to the principle discussed. If a voltage V is applied to the reflective cell, the LC molecules orient themselves in parallel to the electric field for Δε > 0. The linearly polarized light travels downward, is reflected, reaches the polarizer unchanged apart from a phase shift and passes the polarizer. Hence, the reflective cell exhibits the same electro-optical performance as the transmissive cell. The performance is given for the normally black Freedericksz cell with parallel polarizers defined by α = π /4 and Equations (3.73)and (3.85).