(5.26) 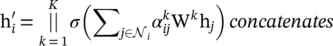
(5.27) 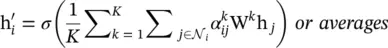
where 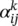 is the normalized attention coefficient computed by the k ‐th attention mechanism. The attention architecture in [35] has several properties: (i) the computation of the node‐neighbor pairs is parallelizable, thus making the operation efficient; (ii) it can be applied to graph nodes with different degrees by specifying arbitrary weights to neighbors; and (iii) it can be easily applied to inductive learning problems.
is the normalized attention coefficient computed by the k ‐th attention mechanism. The attention architecture in [35] has several properties: (i) the computation of the node‐neighbor pairs is parallelizable, thus making the operation efficient; (ii) it can be applied to graph nodes with different degrees by specifying arbitrary weights to neighbors; and (iii) it can be easily applied to inductive learning problems.
Apart from different variants of GNNs, several general frameworks have been proposed that aim to integrate different models into a single framework.
Message passing neural networks ( MPNNs ) [36]: This framework abstracts the commonalities between several of the most popular models for graph‐structured data, such as spectral approaches and non‐spectral approaches in graph convolution, gated GNNs, interaction networks, molecular graph convolutions, and deep tensor neural networks. The model contains two phases, a message passing phase and a readout phase . The message passing phase (namely, the propagation step) runs for T time steps and is defined in terms of th message function M tand the vertex update function U t. Using messages 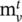 , the updating functions of the hidden states
, the updating functions of the hidden states 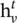 are
are
(5.28) 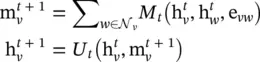
where e vwrepresents features of the edge from node v to w . The readout phase computes a feature vector for the whole graph using the readout function R according to
(5.29) 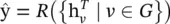
where T denotes the total time steps. The message function M t, vertex update function U t, and readout function R could have different settings. Hence, the MPNN framework could generalize several different models via different function settings. Here, we give an example of generalizing GGNN, and other models’ function settings could be found in Eq. (5.36). The function settings for GGNNs are
(5.30) 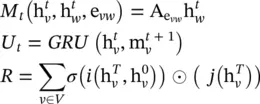
where 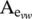 is the adjacency matrix, one for each edge label e . The is the gated recurrent unit introduced in [25]. i and j are neural networks in function R .
is the adjacency matrix, one for each edge label e . The is the gated recurrent unit introduced in [25]. i and j are neural networks in function R .
Non‐local neural networks ( NLNN ) are proposed for capturing long‐range dependencies with deep neural networks by computing the response at a position as a weighted sum of the features at all positions (in space, time, or spacetime). The generic non‐local operation is defined as
(5.31) 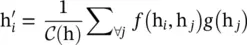
where i is the index of an output position, and j is the index that enumerates all possible positions. f (h i, h j) computes a scalar between i and j representing the relation between them. g (h j) denotes a transformation of the input h j, and a factor 1/ 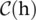 is utilized to normalize the results.
is utilized to normalize the results.
There are several instantiations with different f and g settings. For simplicity, the linear transformation can be used as the function g . That means g (h j) = W gh j, where W gis a learned weight matrix. The Gaussian function is a natural choice for function f , giving 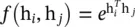 , where
, where 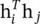 is dot‐product similarity and C (h) =∑ ∀j f (h i, h j). It is straightforward to extend the Gaussian function by computing similarity in the embedding space giving
is dot‐product similarity and C (h) =∑ ∀j f (h i, h j). It is straightforward to extend the Gaussian function by computing similarity in the embedding space giving 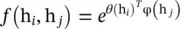 with θ (h i) = W θh i, φ(h j) = W φh j, and
with θ (h i) = W θh i, φ(h j) = W φh j, and 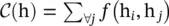 . The function f can also be implemented as a dot‐product similarity f (h i, h j) = θ (h i) Tφ(h j). Here, the factor
. The function f can also be implemented as a dot‐product similarity f (h i, h j) = θ (h i) Tφ(h j). Here, the factor 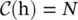 , where N is the number of positions in h. Concatenation can also be used, defined as
, where N is the number of positions in h. Concatenation can also be used, defined as 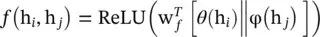 , where w fis a weight vector projecting the vector to a scalar and
, where w fis a weight vector projecting the vector to a scalar and 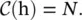
The Graph Network (GN) framework [37] generalizes and extends various GNN, MPNN, and NLNN approaches. A graph is defined as a 3‐tuple G = (u, H , E ) ( H is used instead of V for notational consistency). u is a global attribute, 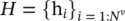 is the set of nodes (of cardinality N v), where each h iis a node’s attribute.
is the set of nodes (of cardinality N v), where each h iis a node’s attribute. 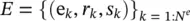 is the set of edges (of cardinality N e), where each e kis the edge’s attribute, r kis the index of the receiver node, and s kis the index of the sender node.
is the set of edges (of cardinality N e), where each e kis the edge’s attribute, r kis the index of the receiver node, and s kis the index of the sender node.
Читать дальше

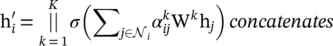
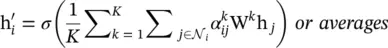
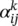 is the normalized attention coefficient computed by the k ‐th attention mechanism. The attention architecture in [35] has several properties: (i) the computation of the node‐neighbor pairs is parallelizable, thus making the operation efficient; (ii) it can be applied to graph nodes with different degrees by specifying arbitrary weights to neighbors; and (iii) it can be easily applied to inductive learning problems.
is the normalized attention coefficient computed by the k ‐th attention mechanism. The attention architecture in [35] has several properties: (i) the computation of the node‐neighbor pairs is parallelizable, thus making the operation efficient; (ii) it can be applied to graph nodes with different degrees by specifying arbitrary weights to neighbors; and (iii) it can be easily applied to inductive learning problems.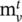 , the updating functions of the hidden states
, the updating functions of the hidden states 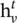 are
are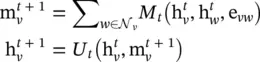
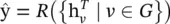
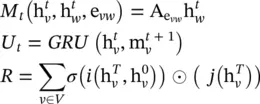
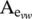 is the adjacency matrix, one for each edge label e . The is the gated recurrent unit introduced in [25]. i and j are neural networks in function R .
is the adjacency matrix, one for each edge label e . The is the gated recurrent unit introduced in [25]. i and j are neural networks in function R .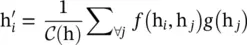
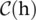 is utilized to normalize the results.
is utilized to normalize the results.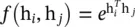 , where
, where 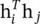 is dot‐product similarity and C (h) =∑ ∀j f (h i, h j). It is straightforward to extend the Gaussian function by computing similarity in the embedding space giving
is dot‐product similarity and C (h) =∑ ∀j f (h i, h j). It is straightforward to extend the Gaussian function by computing similarity in the embedding space giving 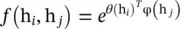 with θ (h i) = W θh i, φ(h j) = W φh j, and
with θ (h i) = W θh i, φ(h j) = W φh j, and 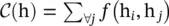 . The function f can also be implemented as a dot‐product similarity f (h i, h j) = θ (h i) Tφ(h j). Here, the factor
. The function f can also be implemented as a dot‐product similarity f (h i, h j) = θ (h i) Tφ(h j). Here, the factor 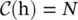 , where N is the number of positions in h. Concatenation can also be used, defined as
, where N is the number of positions in h. Concatenation can also be used, defined as 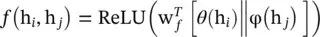 , where w fis a weight vector projecting the vector to a scalar and
, where w fis a weight vector projecting the vector to a scalar and 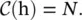
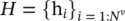 is the set of nodes (of cardinality N v), where each h iis a node’s attribute.
is the set of nodes (of cardinality N v), where each h iis a node’s attribute. 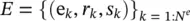 is the set of edges (of cardinality N e), where each e kis the edge’s attribute, r kis the index of the receiver node, and s kis the index of the sender node.
is the set of edges (of cardinality N e), where each e kis the edge’s attribute, r kis the index of the receiver node, and s kis the index of the sender node.










