Note that any symmetric function could be used in place of the max ‐pooling operation here. The operation of GraphSAGE is illustrated in Figure 5.1[23].
Gate: Several works have attempted to use a gate mechanism such as gate recurrent units (GRUs) [25] or LSTM [26] in the propagation step to mitigate the restrictions in the former GNN models and improve the long‐term propagation of information across the graph structure.
Gated graph neural network ( GGNN ) [27] uses GRUs in the propagation step, unrolls the recurrence for a fixed number of steps T , and uses backpropagation through time in order to compute gradients. So, the propagation model can be presented as
(5.20) 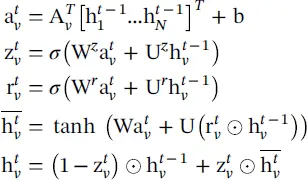
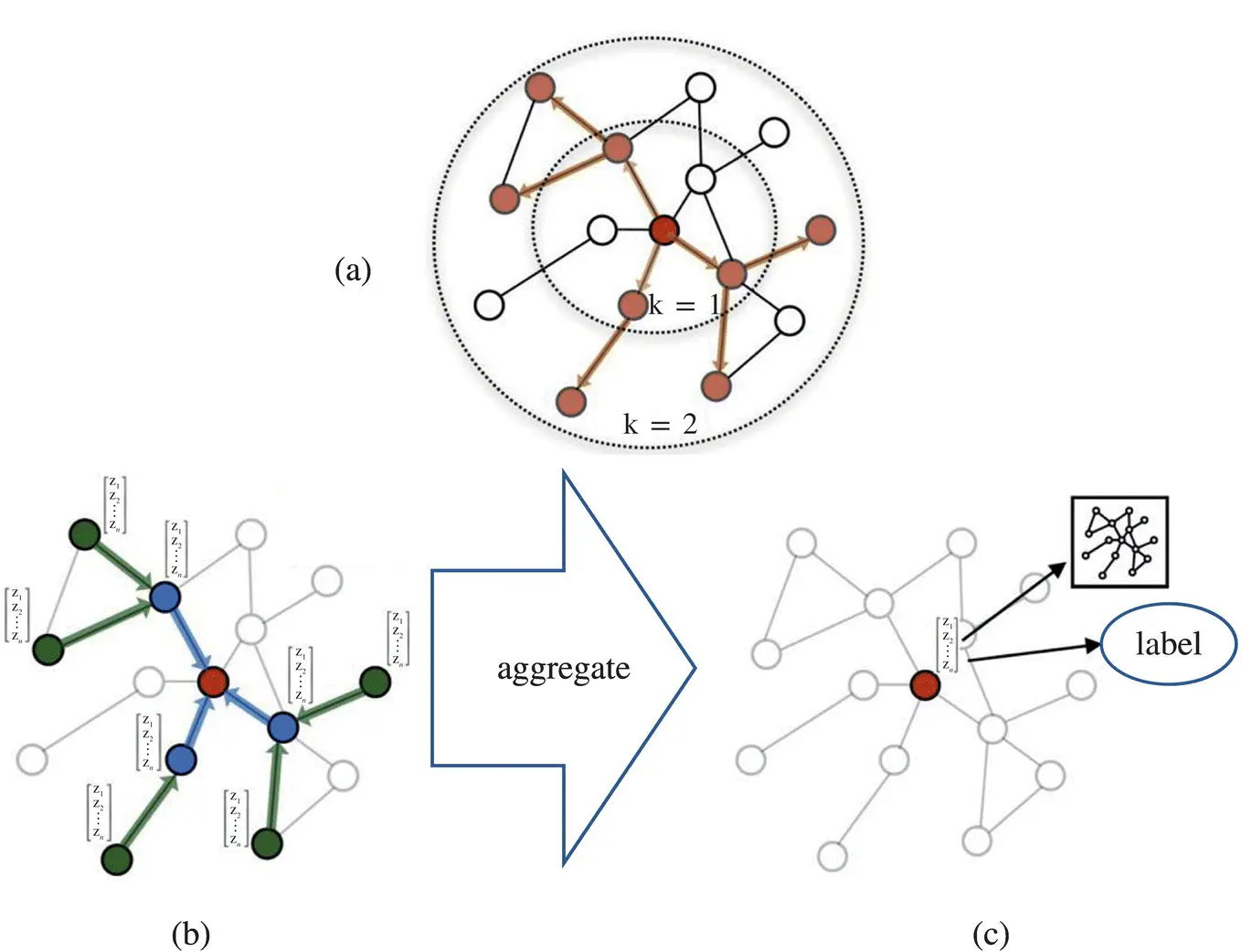
Figure 5.1 Operation of GraphSAGE: (a) sample neighborhood, (b) aggregate feature information from neighbors, (c) predict graph context and label using aggregated information.
Source: Hamilton et al. [23].
The node v first aggregates message from its neighbors, where A vis the submatrix of the graph adjacency matrix A and denotes the connection of node v with its neighbors. The GRU‐like update functions incorporate information from the other nodes and from the previous time step to update each node’s hidden state. Matrix a gathers the neighborhood information of node v , and z and r are the update and reset gates.
LSTM architecture extensions , referred to as the Child ‐ Sum Tree‐LSTM and the N ‐ ary Tree‐LSTM , are presented in [28]. As in standard LSTM units, each Tree‐LSTM unit (indexed by v ) contains input and output gates i vand o v, a memory cell c v, and a hidden state h v. Instead of a single forget gate, the Tree‐LSTM unit contains one forget gate f vkfor each child k , allowing the unit to selectively incorporate information from each child. The Child‐Sum Tree‐LSTM transition equations are given as
(5.21) 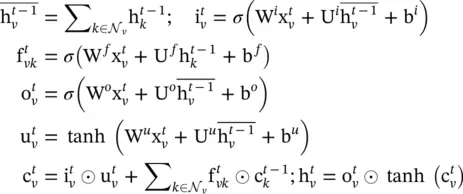
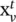 is the input vector at time t in the standard LSTM setting. If the branching factor of a tree is at most K and all children of a node are ordered, – that is, they can be indexed from 1 to K – then the N ‐ary Tree‐LSTM can be used. For node v ,
is the input vector at time t in the standard LSTM setting. If the branching factor of a tree is at most K and all children of a node are ordered, – that is, they can be indexed from 1 to K – then the N ‐ary Tree‐LSTM can be used. For node v , 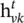 and
and 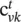 denote the hidden state and memory cell of its k ‐th child at time t , respectively. The transition equations are now
denote the hidden state and memory cell of its k ‐th child at time t , respectively. The transition equations are now
(5.22) 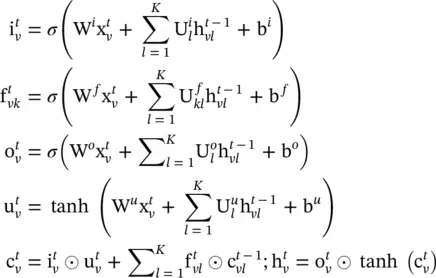
The introduction of separate parameter matrices for each child k allows the model to learn more fine‐grained representations conditioning on the states of a unit’s children than the Child‐Sum Tree‐LSTM.
The two types of Tree‐LSTMs can be easily adapted to the graph. The graph‐structured LSTM in [29] is an example of the N ‐ary Tree‐LSTM applied to the graph. However, it is a simplified version since each node in the graph has at most two incoming edges (from its parent and sibling predecessor). Reference [30] proposed another variant of the Graph LSTM based on the relation extraction task. The main difference between graphs and trees is that edges of graphs have labels. Work in [30] utilizes different weight matrices to represent different labels:
(5.23) 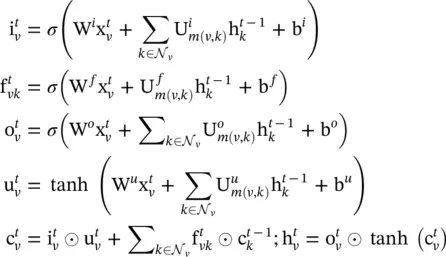
where m ( v , k ) denotes the edge label between node v and k .
The attention mechanism has been successfully used in many sequence‐based tasks such as machine translation [31–33] and machine reading [34]. Work in [35] proposed a graph attention network (GAT) that incorporates the attention mechanism into the propagation step. It computes the hidden states of each node by attending to its neighbors, following a self ‐ attention strategy. The work defines a single graph attentional layer and constructs arbitrary GATs by stacking this layer. The layer computes the coefficients in the attention mechanism of the node pair ( i , j ) by
(5.24) 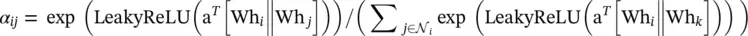
where α ijis the attention coefficient of node j to 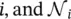 represents the neighborhoods of node i in the graph. The input set of node features to the layer is h = {h 1, h 2, …, h N}, h i∈ ℝ F, where N is the number of nodes, and F is the number of features of each node; the layer produces a new set of node features (of potentially different cardinality F ′),
represents the neighborhoods of node i in the graph. The input set of node features to the layer is h = {h 1, h 2, …, h N}, h i∈ ℝ F, where N is the number of nodes, and F is the number of features of each node; the layer produces a new set of node features (of potentially different cardinality F ′), 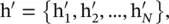
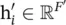 , as its output.
, as its output. 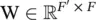 is the weight matrix of a shared linear transformation that is applied to every node, and
is the weight matrix of a shared linear transformation that is applied to every node, and 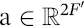 is the weight vector of a single‐layer FNN. It is normalized by a softmax function, and the LeakyReLU nonlinearity (with negative input slope α = 0.2) is applied. After applying a nonlinearity, the final output features of each node can be obtained as
is the weight vector of a single‐layer FNN. It is normalized by a softmax function, and the LeakyReLU nonlinearity (with negative input slope α = 0.2) is applied. After applying a nonlinearity, the final output features of each node can be obtained as
(5.25) 
The layer utilizes multi ‐ head attention similarly to [33] to stabilize the learning process. It applies K independent attention mechanisms to compute the hidden states and then concatenates their features (or computes the average), resulting in the following two output representations:
Читать дальше

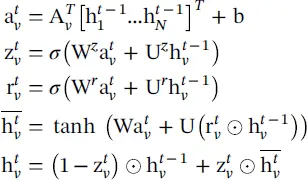

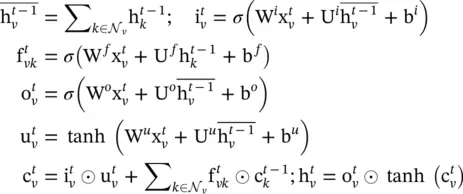
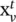 is the input vector at time t in the standard LSTM setting. If the branching factor of a tree is at most K and all children of a node are ordered, – that is, they can be indexed from 1 to K – then the N ‐ary Tree‐LSTM can be used. For node v ,
is the input vector at time t in the standard LSTM setting. If the branching factor of a tree is at most K and all children of a node are ordered, – that is, they can be indexed from 1 to K – then the N ‐ary Tree‐LSTM can be used. For node v , 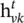 and
and 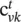 denote the hidden state and memory cell of its k ‐th child at time t , respectively. The transition equations are now
denote the hidden state and memory cell of its k ‐th child at time t , respectively. The transition equations are now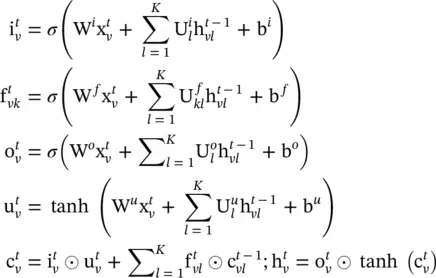
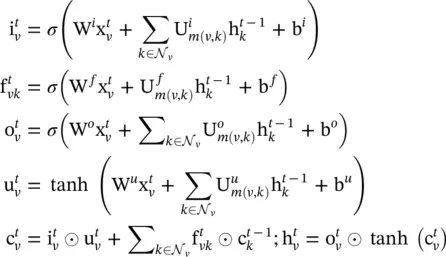
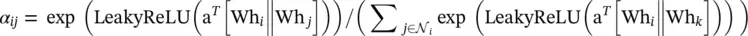
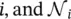 represents the neighborhoods of node i in the graph. The input set of node features to the layer is h = {h 1, h 2, …, h N}, h i∈ ℝ F, where N is the number of nodes, and F is the number of features of each node; the layer produces a new set of node features (of potentially different cardinality F ′),
represents the neighborhoods of node i in the graph. The input set of node features to the layer is h = {h 1, h 2, …, h N}, h i∈ ℝ F, where N is the number of nodes, and F is the number of features of each node; the layer produces a new set of node features (of potentially different cardinality F ′), 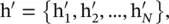
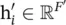 , as its output.
, as its output. 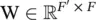 is the weight matrix of a shared linear transformation that is applied to every node, and
is the weight matrix of a shared linear transformation that is applied to every node, and 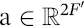 is the weight vector of a single‐layer FNN. It is normalized by a softmax function, and the LeakyReLU nonlinearity (with negative input slope α = 0.2) is applied. After applying a nonlinearity, the final output features of each node can be obtained as
is the weight vector of a single‐layer FNN. It is normalized by a softmax function, and the LeakyReLU nonlinearity (with negative input slope α = 0.2) is applied. After applying a nonlinearity, the final output features of each node can be obtained as











