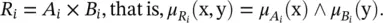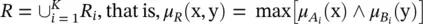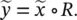A descriptive (linguistic) fuzzy model captures qualitative knowledge in the form of if‐then rules [106]:
(4.31) 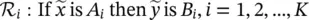
Here, 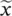 is the input (antecedent) linguistic variable, and A iare the antecedent descriptive (linguistic) terms (constants). Similarly,
is the input (antecedent) linguistic variable, and A iare the antecedent descriptive (linguistic) terms (constants). Similarly, 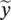 is the output (consequent) linguistic variable, and B iare the consequent linguistic terms. The values of
is the output (consequent) linguistic variable, and B iare the consequent linguistic terms. The values of 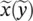 and the linguistic terms A i( B i) are fuzzy sets defined in the domains of their respective base variables: x ∈ X ⊂ R pand y ∈ Y ⊂ R q. The membership functions of the antecedent (consequent) fuzzy sets are then the mappings: μ (x) : X → [0, 1], μ (y) : Y → [0, 1]. Fuzzy sets A idefine fuzzy regions in the antecedent space, for which the respective consequent propositions hold. The linguistic terms A iand B iare usually selected from sets of predefined terms, such as Small, Medium, and so on. By denoting these sets by
and the linguistic terms A i( B i) are fuzzy sets defined in the domains of their respective base variables: x ∈ X ⊂ R pand y ∈ Y ⊂ R q. The membership functions of the antecedent (consequent) fuzzy sets are then the mappings: μ (x) : X → [0, 1], μ (y) : Y → [0, 1]. Fuzzy sets A idefine fuzzy regions in the antecedent space, for which the respective consequent propositions hold. The linguistic terms A iand B iare usually selected from sets of predefined terms, such as Small, Medium, and so on. By denoting these sets by 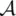 and
and 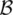 , respectively, we have
, respectively, we have 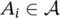 and
and 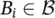 . The rule base
. The rule base 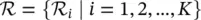 and the sets
and the sets 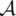 and
and 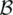 constitute the knowledgebase of the linguistic model.
constitute the knowledgebase of the linguistic model.
Consider a simple fuzzy model that qualitatively describes how the throughput in data network using the Aloha protocol depends on the traffic volume. We have a scalar input – the traffic volume ( x ) – and a scalar output – the network throughput ( y ). Define the set of antecedent linguistic terms: 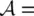 {Low, Moderate, High}= {L, M, H}, and the set of consequent linguistic terms:
{Low, Moderate, High}= {L, M, H}, and the set of consequent linguistic terms: 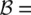 {Low, High} = {L, H}. The qualitative relationship between the model input and output can be expressed by the following rules:
{Low, High} = {L, H}. The qualitative relationship between the model input and output can be expressed by the following rules:
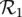 : If the traffic volume is Low‚ then the network throughput is Low.
: If the traffic volume is Low‚ then the network throughput is Low.
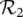 : If the traffic volume is Moderate‚ then the network throughput is High.
: If the traffic volume is Moderate‚ then the network throughput is High.
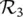 : If the traffic volume is High‚ then the network throughput is Low (due to the excessive collisions).
: If the traffic volume is High‚ then the network throughput is Low (due to the excessive collisions).
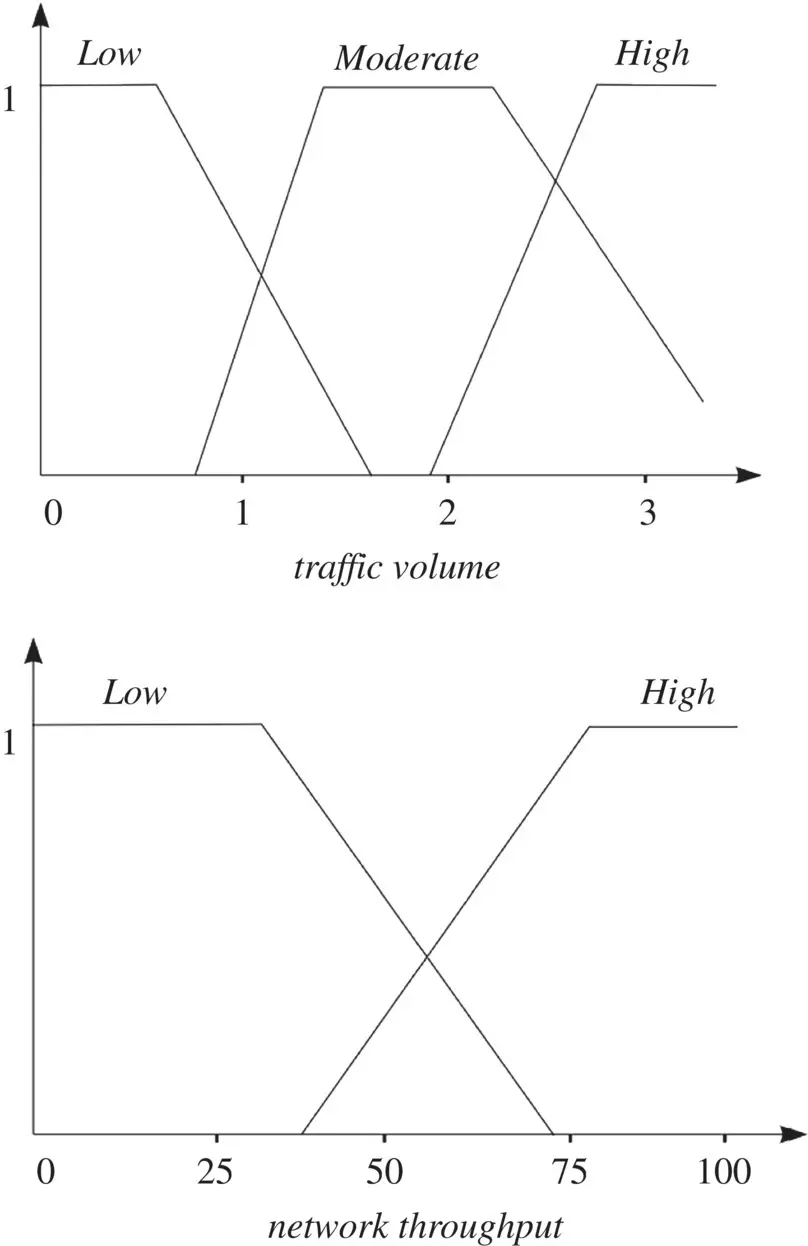
Figure 4.4 Example of membership functions versus the traffic volume and network throughput.
The meaning of the linguistic terms is defined by their membership functions, depicted in Figure 4.4. The numerical values along the base variables are selected somewhat arbitrarily. Note that no universal meaning of the linguistic terms can be defined. For this example, it will depend on the type of the traffic, network size and the topology, MAC protocol, and so on. Nevertheless, the qualitative relationship expressed by the rules remains valid.
Relational representation of a linguistic model: Each rule in Eq. (4.31)can be regarded as a fuzzy relation (fuzzy restriction on the simultaneous occurrences of values x and y): R i: ( X × Y ) → [0, 1]. This relation can be computed in two basic ways: by using fuzzy conjunctions and by using fuzzy implications (fuzzy logic method). Fuzzy implications are used when the if‐then rule, Eq. (4.31), is strictly regarded as an implication A i→ B i, that is, “ A implies B .” In classical logic, this means that if A holds, B must hold as well for the implication to be true. Nothing can, however, be said about B when A does not hold, and the relationship also cannot be inverted.
When using a conjunction, A ∧ B , the interpretation of the if‐then rules is “it is true that A and B simultaneously hold.” This relationship is symmetric and can be inverted. For simplicity, in this text we restrict ourselves to the conjunction method. The relation R is computed by the minimum (∧) operator:
(4.32) 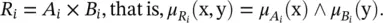
Note that the minimum is computed on the Cartesian product space of X and Y , that is, for all possible pairs of x and y. The fuzzy relation R representing the entire model, Eq. (4.31), is given by the disjunction (union) of the K individual rule’s relations R i:
(4.33) 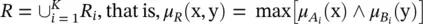
Now the entire rule base is encoded in the fuzzy relation R , and the output of the linguistic model can be computed by the relational max‐min composition (∘):
(4.34) 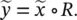
Let us compute the fuzzy relation for the linguistic model of Figure 4.4. First, we discretize the input and output domains, for instance: X = {0, 1, 2, 3} and Y = {0,25,50,75,100}. The (discrete) membership functions are given in Table 4.1for both antecedent linguistic terms, and for the consequent terms.
Table 4.1 An example of the (discrete) membership functions for both antecedent linguistic terms, and for the consequent terms.
Читать дальше

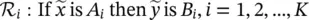
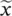 is the input (antecedent) linguistic variable, and A iare the antecedent descriptive (linguistic) terms (constants). Similarly,
is the input (antecedent) linguistic variable, and A iare the antecedent descriptive (linguistic) terms (constants). Similarly, 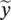 is the output (consequent) linguistic variable, and B iare the consequent linguistic terms. The values of
is the output (consequent) linguistic variable, and B iare the consequent linguistic terms. The values of 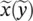 and the linguistic terms A i( B i) are fuzzy sets defined in the domains of their respective base variables: x ∈ X ⊂ R pand y ∈ Y ⊂ R q. The membership functions of the antecedent (consequent) fuzzy sets are then the mappings: μ (x) : X → [0, 1], μ (y) : Y → [0, 1]. Fuzzy sets A idefine fuzzy regions in the antecedent space, for which the respective consequent propositions hold. The linguistic terms A iand B iare usually selected from sets of predefined terms, such as Small, Medium, and so on. By denoting these sets by
and the linguistic terms A i( B i) are fuzzy sets defined in the domains of their respective base variables: x ∈ X ⊂ R pand y ∈ Y ⊂ R q. The membership functions of the antecedent (consequent) fuzzy sets are then the mappings: μ (x) : X → [0, 1], μ (y) : Y → [0, 1]. Fuzzy sets A idefine fuzzy regions in the antecedent space, for which the respective consequent propositions hold. The linguistic terms A iand B iare usually selected from sets of predefined terms, such as Small, Medium, and so on. By denoting these sets by 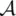 and
and 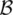 , respectively, we have
, respectively, we have 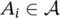 and
and 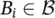 . The rule base
. The rule base 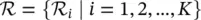 and the sets
and the sets 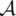 and
and 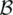 constitute the knowledgebase of the linguistic model.
constitute the knowledgebase of the linguistic model.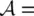 {Low, Moderate, High}= {L, M, H}, and the set of consequent linguistic terms:
{Low, Moderate, High}= {L, M, H}, and the set of consequent linguistic terms: 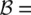 {Low, High} = {L, H}. The qualitative relationship between the model input and output can be expressed by the following rules:
{Low, High} = {L, H}. The qualitative relationship between the model input and output can be expressed by the following rules: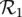 : If the traffic volume is Low‚ then the network throughput is Low.
: If the traffic volume is Low‚ then the network throughput is Low.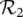 : If the traffic volume is Moderate‚ then the network throughput is High.
: If the traffic volume is Moderate‚ then the network throughput is High.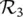 : If the traffic volume is High‚ then the network throughput is Low (due to the excessive collisions).
: If the traffic volume is High‚ then the network throughput is Low (due to the excessive collisions).