Savo G. Glisic - Artificial Intelligence and Quantum Computing for Advanced Wireless Networks
Здесь есть возможность читать онлайн «Savo G. Glisic - Artificial Intelligence and Quantum Computing for Advanced Wireless Networks» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Artificial Intelligence and Quantum Computing for Advanced Wireless Networks
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Artificial Intelligence and Quantum Computing for Advanced Wireless Networks: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Artificial Intelligence and Quantum Computing for Advanced Wireless Networks»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
A practical overview of the implementation of artificial intelligence and quantum computing technology in large-scale communication networks Artificial Intelligence and Quantum Computing for Advanced Wireless Networks
Artificial Intelligence and Quantum Computing for Advanced Wireless Networks

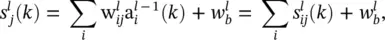
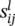 are defined for convenience. The partial derivative
are defined for convenience. The partial derivative 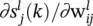 in Eq. (3.21)is easily evaluated as
in Eq. (3.21)is easily evaluated as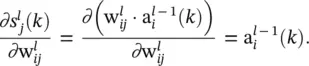
 allows us to rewrite Eq. (3.21)as
allows us to rewrite Eq. (3.21)as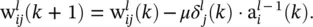
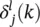 . Starting with the output layer, we observe that
. Starting with the output layer, we observe that 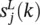 influences only the instantaneous output node error e j( k ). Thus, we have
influences only the instantaneous output node error e j( k ). Thus, we have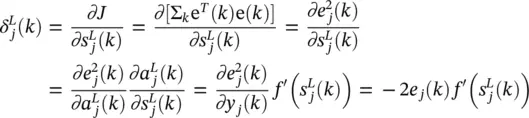
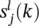 has an impact on the error indirectly through all node values
has an impact on the error indirectly through all node values 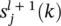 in the subsequent layer. Due to the tap delay lines,
in the subsequent layer. Due to the tap delay lines, 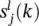 also has an impact on the error across time. Therefore, the chain rule now becomes
also has an impact on the error across time. Therefore, the chain rule now becomes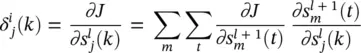
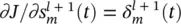 . Continuing with the remaining term
. Continuing with the remaining term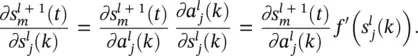
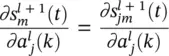
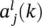 has on
has on 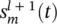 is via the synapse connecting unit j in layer l to unit m in layer l + 1. The definition of the synapse is explicitly given as
is via the synapse connecting unit j in layer l to unit m in layer l + 1. The definition of the synapse is explicitly given as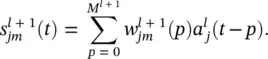
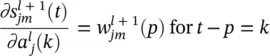
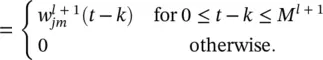
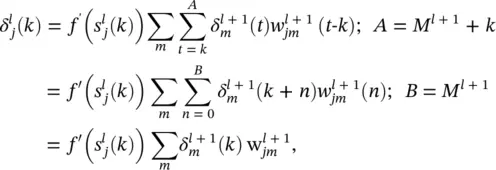
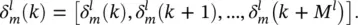
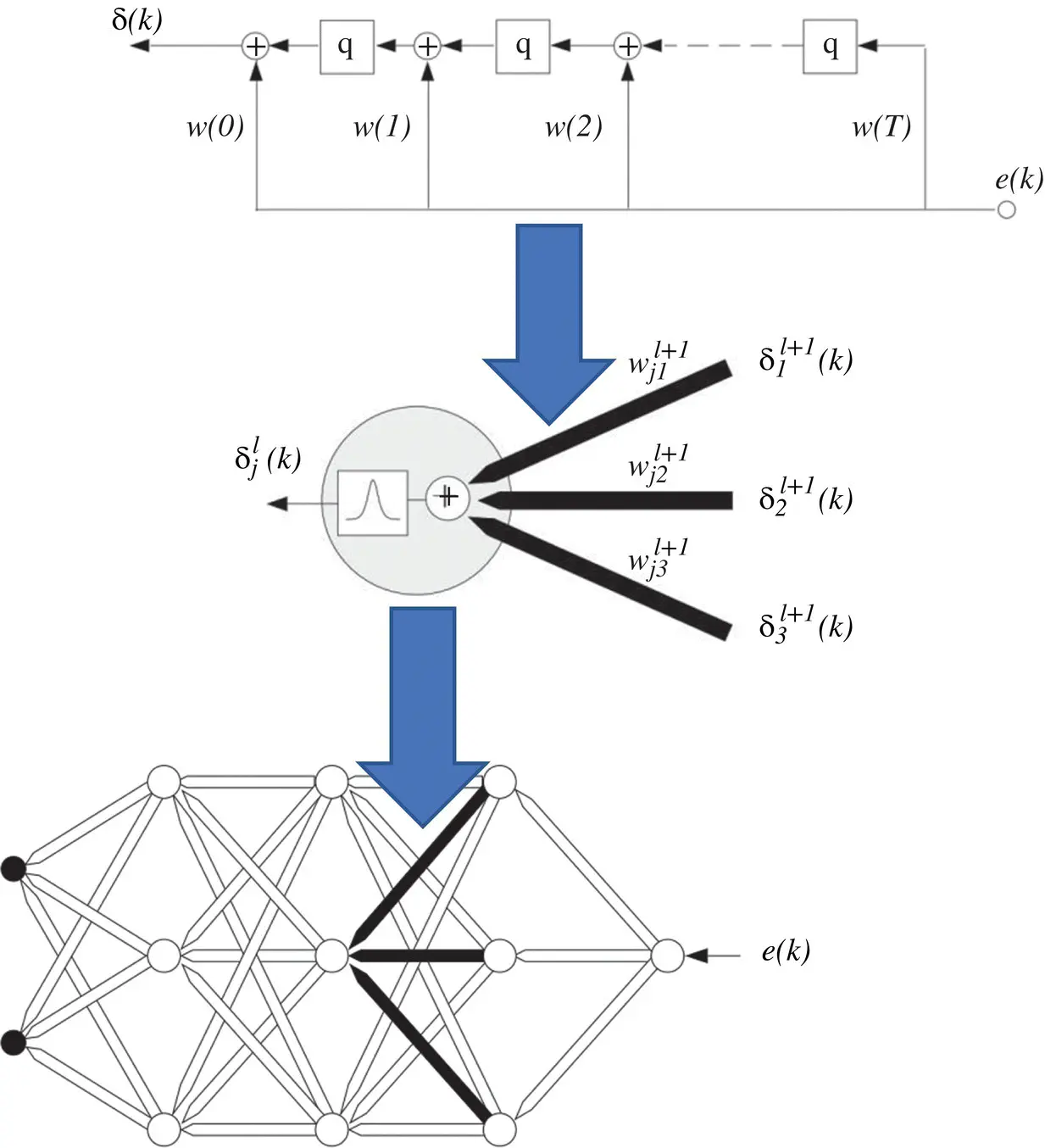
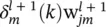 within the sum corresponds to a reverse FIR filter. This is illustrated in Figure 3.7. The filter is drawn in such a way to emphasize the reversal of signal propagation through the FIR. Representing the forward propagation of states and the backward propagation of error terms requires simply reversing the direction of signal flow. In this process, unit delay operators q −1should be replaced with unit advances q +1. The complete adaptation algorithm can be summarized as follows:
within the sum corresponds to a reverse FIR filter. This is illustrated in Figure 3.7. The filter is drawn in such a way to emphasize the reversal of signal propagation through the FIR. Representing the forward propagation of states and the backward propagation of error terms requires simply reversing the direction of signal flow. In this process, unit delay operators q −1should be replaced with unit advances q +1. The complete adaptation algorithm can be summarized as follows: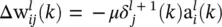
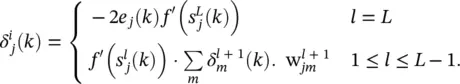
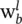 may again be adapted by letting
may again be adapted by letting 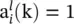 in Eq. (3.33). Observe the similarities between these equations and those for standard backpropagation. In fact, by replacing the vectors a, w, and δ by scalars, the previous equations reduce to precisely the backpropagation algorithm for static networks. Differences in the temporal version are due to implicit time relations. To find
in Eq. (3.33). Observe the similarities between these equations and those for standard backpropagation. In fact, by replacing the vectors a, w, and δ by scalars, the previous equations reduce to precisely the backpropagation algorithm for static networks. Differences in the temporal version are due to implicit time relations. To find 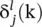 , we filter the δ’s from the next layer backward through the FIR (see Figure 3.7). In other words, δ’s are created not only by taking weighted sums, but also by backward filtering. For each x(k) and desired vector d(k), the forward filters are incremented one time step, producing the current output y(k) and corresponding error e(k). Next, the backward filters are incremented one time step, advancing the δ(k) terms and allowing the filter coefficients to be updated. The process is then repeated for a new input at time k + 1.
, we filter the δ’s from the next layer backward through the FIR (see Figure 3.7). In other words, δ’s are created not only by taking weighted sums, but also by backward filtering. For each x(k) and desired vector d(k), the forward filters are incremented one time step, producing the current output y(k) and corresponding error e(k). Next, the backward filters are incremented one time step, advancing the δ(k) terms and allowing the filter coefficients to be updated. The process is then repeated for a new input at time k + 1.










