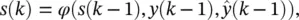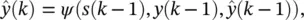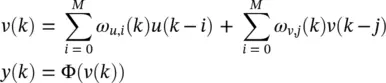(3.54) 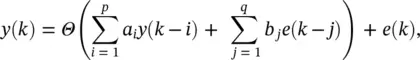
where Θ (·) is an unknown differentiable zero‐memory nonlinear function. Notice e ( k ) is not included within Θ (·) as it is unobservable. The term NARMA ( p , q ) is adopted to define Eq. (3.54), since except for the ( k ), the output of an ARMA ( p , q ) model is simply passed through the zero‐memory nonlinearity Θ (·).
The corresponding NARMA ( p , q ) predictor is given by
(3.55) 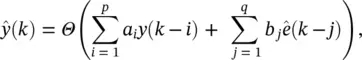
where the residuals ê 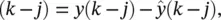 j = 1, 2, … , q . Equivalently, the simplest form of nonlinear autoregressive (NAR( p )) model is described by
j = 1, 2, … , q . Equivalently, the simplest form of nonlinear autoregressive (NAR( p )) model is described by
(3.56) 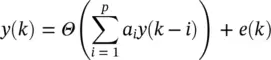
and its associated predictor is
(3.57) 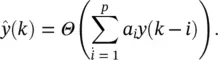
The two predictors are shown together in Figure 3.10, where it is clearly indicated which parts are included in a particular scheme. In other words, feedback is included within the NARMA ( p , q ) predictor, whereas the NAR( p ) predictor is an entirely feedforward structure. In control applications, most generally, NARMA ( p , q ) models also include also external (exogeneous) inputs, ( k − s ), s = 1, 2, … , r , giving
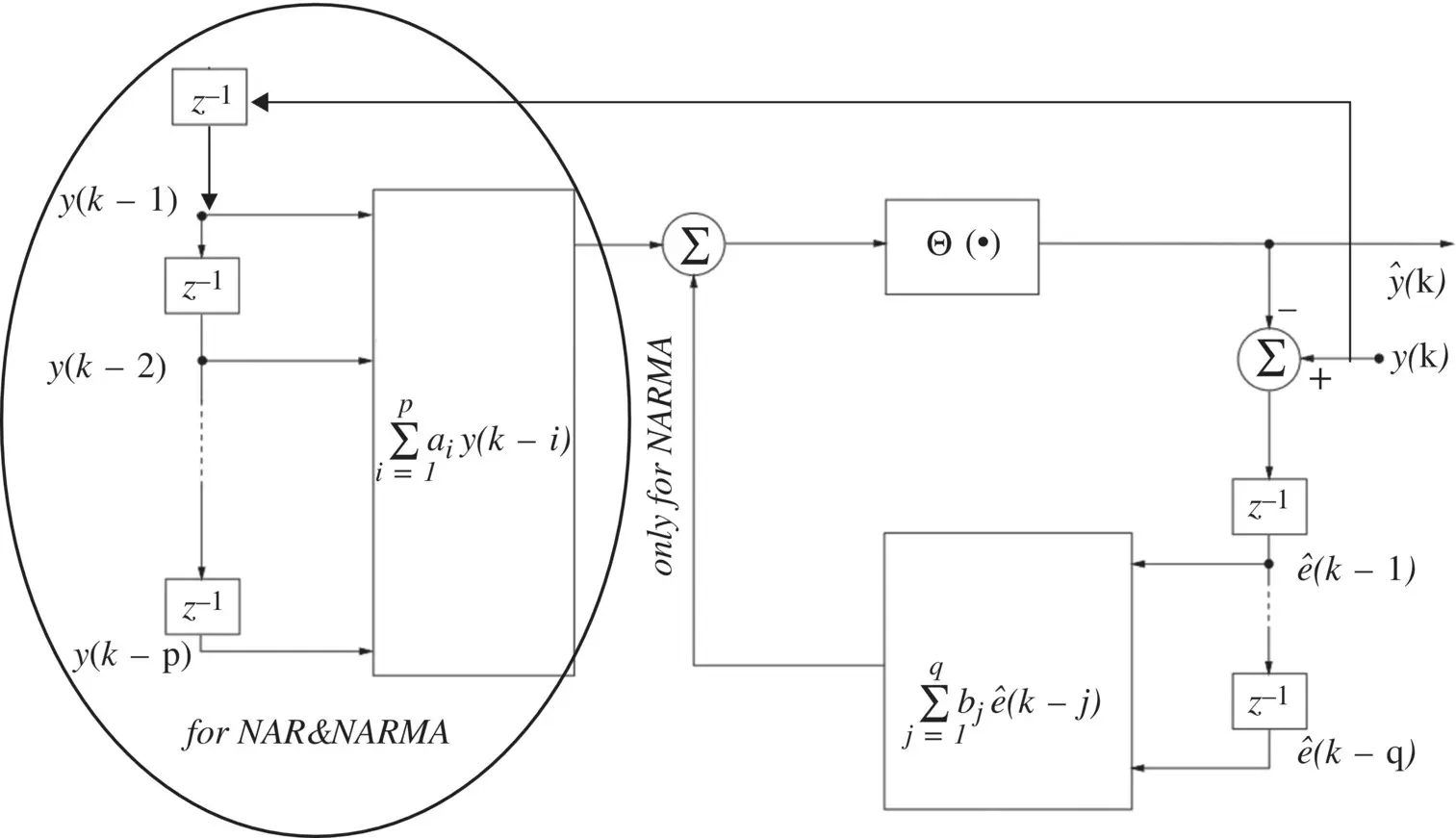
Figure 3.10 Nonlinear AR/ARMA predictors.
(3.58) 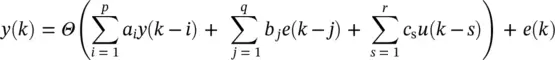
and referred to as a NARMA with exogenous inputs model, NARMAX ( p , q , r ), with associated predictor
(3.59) 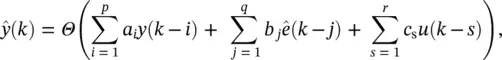
which again exploits feedback.
3.4.2 Feedback Options in Recurrent Neural Networks
Feedbacks in recurrent neural networks: In Figure 3.11, the inputs to the network are drawn from the discrete time signal ( k ). Conceptually, it is straightforward to consider connecting the delayed versions of the output, 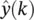 , of the network to its input. Such connections, however, introduce feedback into the network, and therefore the stability of such networks must be considered . The provision of feedback, with delay, introduces memory to the network and so is appropriate for prediction. The feedback within recurrent neural networks can be achieved in either a local or global manner. An example of a recurrent neural network is shown in Figure 3.11with connections for both local and global feedback. The local feedback is achieved by the introduction of feedback within the hidden layer, whereas the global feedback is produced by the connection of the network output to the network input. Interneuron connections can also exist in the hidden layer, but they are not shown in Figure 3.11. Although explicit delays are not shown in the feedback connections, they are assumed to be present within the neurons for the network to be realizable. The operation of a recurrent neural network predictor that employs global feedback can now be represented by
, of the network to its input. Such connections, however, introduce feedback into the network, and therefore the stability of such networks must be considered . The provision of feedback, with delay, introduces memory to the network and so is appropriate for prediction. The feedback within recurrent neural networks can be achieved in either a local or global manner. An example of a recurrent neural network is shown in Figure 3.11with connections for both local and global feedback. The local feedback is achieved by the introduction of feedback within the hidden layer, whereas the global feedback is produced by the connection of the network output to the network input. Interneuron connections can also exist in the hidden layer, but they are not shown in Figure 3.11. Although explicit delays are not shown in the feedback connections, they are assumed to be present within the neurons for the network to be realizable. The operation of a recurrent neural network predictor that employs global feedback can now be represented by
(3.60) 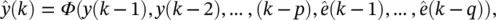
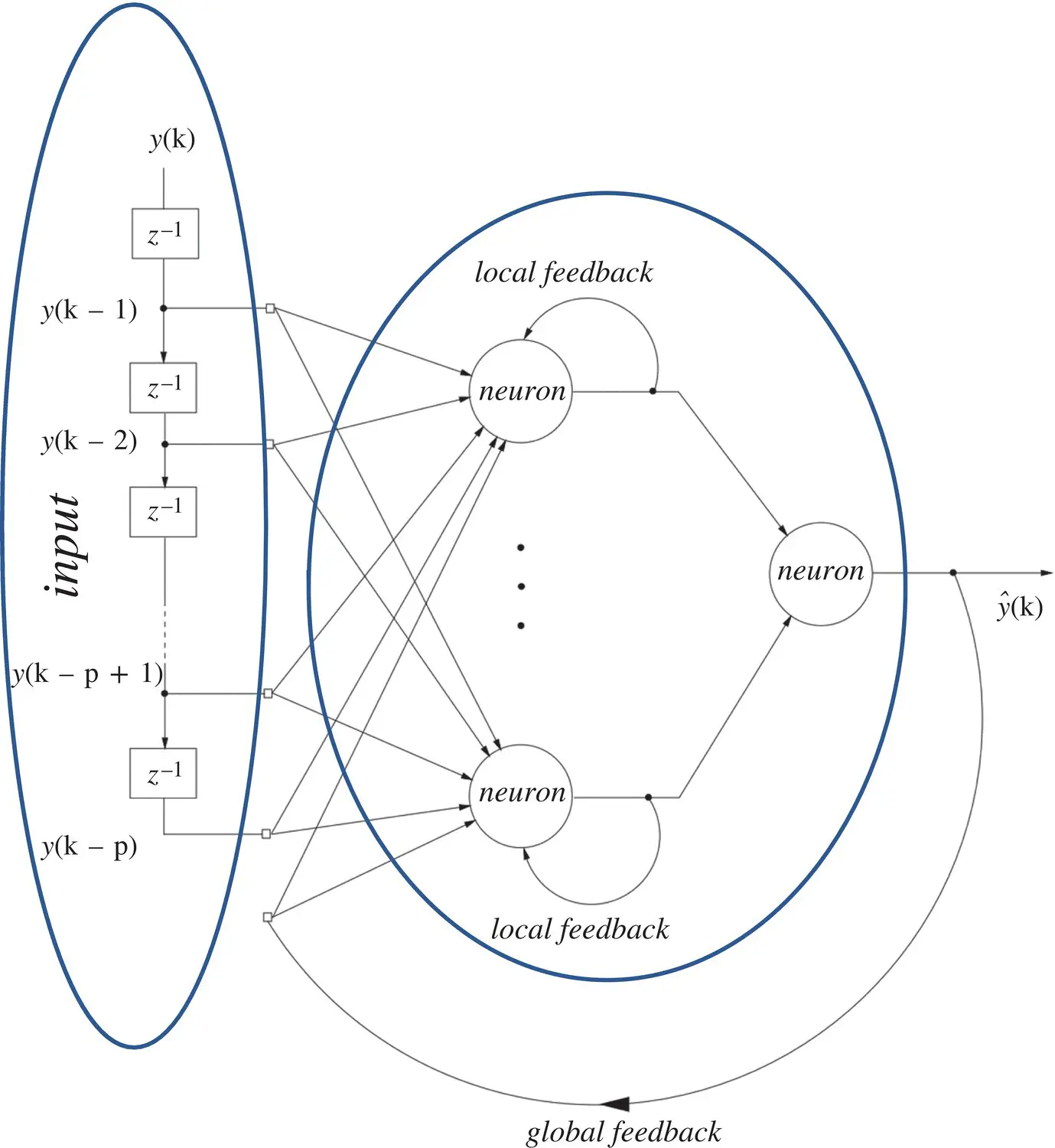
Figure 3.11 Recurrent neural network.
where again Φ (·) represents the nonlinear mapping of the neural network and ê 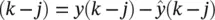 , j = 1, … , q .
, j = 1, … , q .
State‐space representation and canonical form: Any feedback network can be cast into a canonical form that consists of a feedforward (static) network (FFSN) (i) whose outputs are the outputs of the neurons that have the desired values, and the values of the state variables, and (ii) whose inputs are the inputs of the network and the values of the state variables, the latter being delayed by one time unit.
The general canonical form of a recurrent neural network is represented in Figure 3.12. If the state is assumed to contain N variables, then a state vector is defined as s ( k ) = [ s 1( k ), s 2( k ), … , s N( k )] T, and a vector of p external inputs is given by y ( k − 1) = [ y ( k − 1), y ( k − 2), … , y ( k − p )] T. The state evolution and output equations of the recurrent network for prediction are given, respectively, by
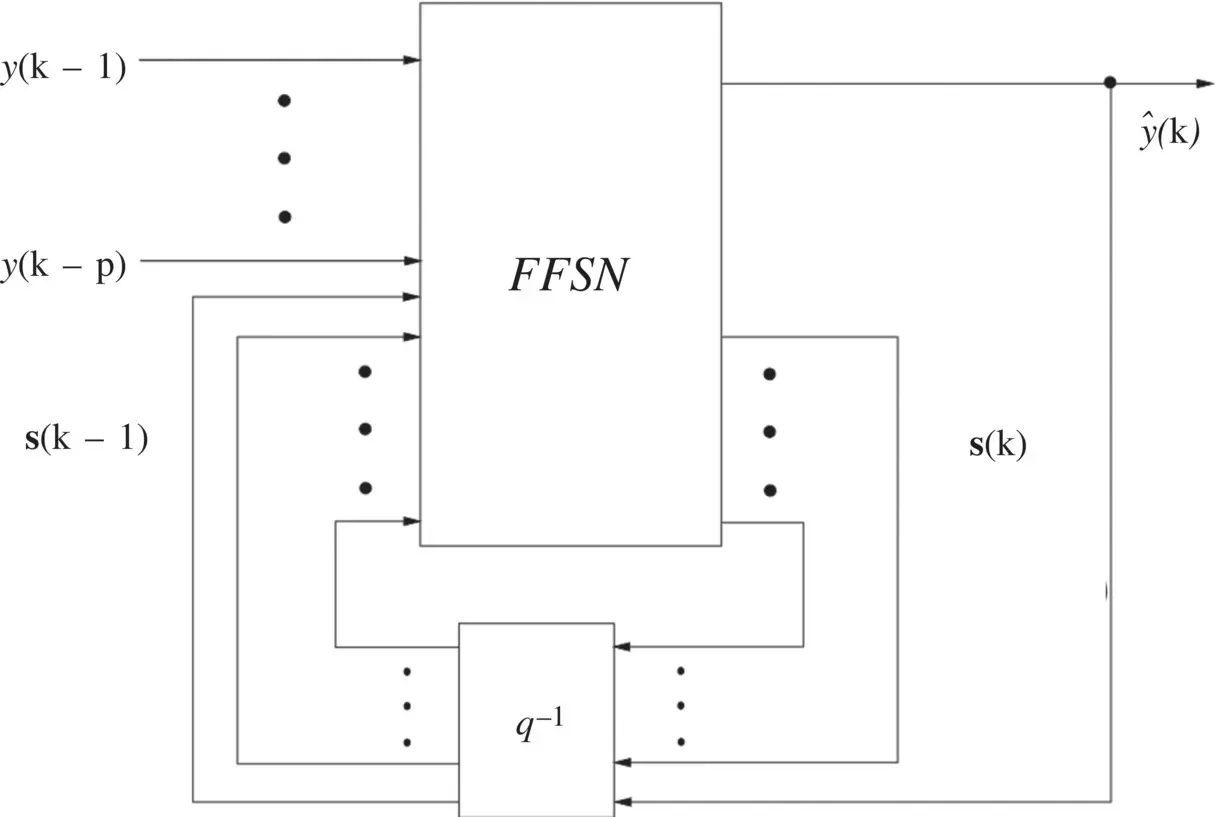
Figure 3.12 Canonical form of a recurrent neural network for prediction.
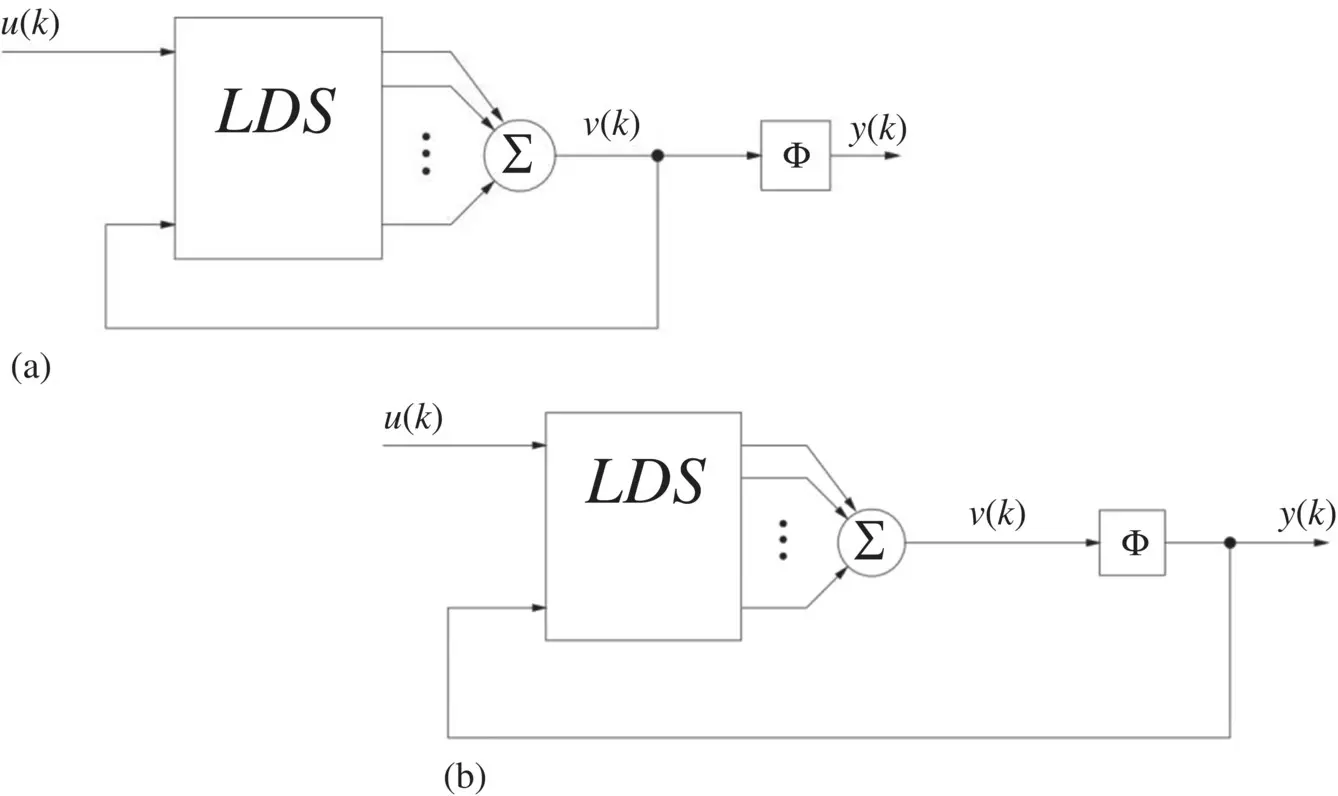
Figure 3.13 Recurrent neural network (RNN) architectures: (a) activation feedback and (b) output feedback.
(3.61) 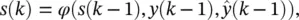
(3.62) 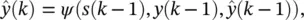
where φ and Ψ represent general classes of nonlinearities.
Recurrent neural network (RNN) architectures: Activation feedback and output feedback are two ways to include recurrent connections in neural networks, as shown in Figure 3.13a and b, respectively.
The output of a neuron shown in Figure 3.13a can be expressed as
(3.63) 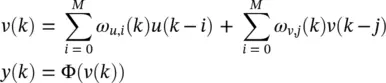
Читать дальше

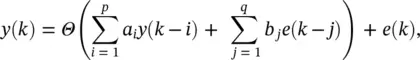
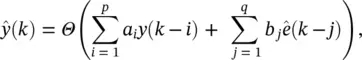
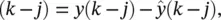 j = 1, 2, … , q . Equivalently, the simplest form of nonlinear autoregressive (NAR( p )) model is described by
j = 1, 2, … , q . Equivalently, the simplest form of nonlinear autoregressive (NAR( p )) model is described by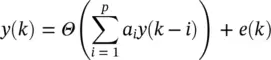
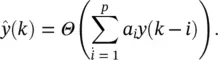

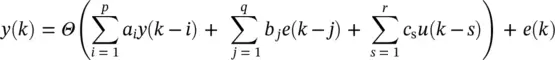
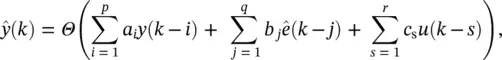
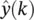 , of the network to its input. Such connections, however, introduce feedback into the network, and therefore the stability of such networks must be considered . The provision of feedback, with delay, introduces memory to the network and so is appropriate for prediction. The feedback within recurrent neural networks can be achieved in either a local or global manner. An example of a recurrent neural network is shown in Figure 3.11with connections for both local and global feedback. The local feedback is achieved by the introduction of feedback within the hidden layer, whereas the global feedback is produced by the connection of the network output to the network input. Interneuron connections can also exist in the hidden layer, but they are not shown in Figure 3.11. Although explicit delays are not shown in the feedback connections, they are assumed to be present within the neurons for the network to be realizable. The operation of a recurrent neural network predictor that employs global feedback can now be represented by
, of the network to its input. Such connections, however, introduce feedback into the network, and therefore the stability of such networks must be considered . The provision of feedback, with delay, introduces memory to the network and so is appropriate for prediction. The feedback within recurrent neural networks can be achieved in either a local or global manner. An example of a recurrent neural network is shown in Figure 3.11with connections for both local and global feedback. The local feedback is achieved by the introduction of feedback within the hidden layer, whereas the global feedback is produced by the connection of the network output to the network input. Interneuron connections can also exist in the hidden layer, but they are not shown in Figure 3.11. Although explicit delays are not shown in the feedback connections, they are assumed to be present within the neurons for the network to be realizable. The operation of a recurrent neural network predictor that employs global feedback can now be represented by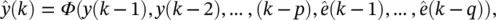

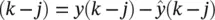 , j = 1, … , q .
, j = 1, … , q .