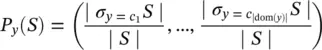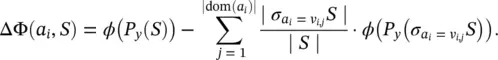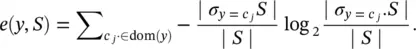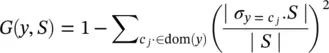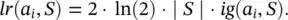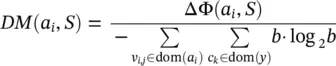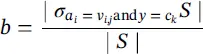A slightly more sophisticated tree for predicting email spam is shown in Figure 2.17. The results for data from 4601 email messages have been presented in [12].

Figure 2.17 Predicting email spam.
Source: Trevor Hastie [12].
Splitting criteria: In most of the cases, the discrete splitting functions are univariate. Univariate means that an internal node is split according to the value of a single attribute. Consequently, the inducer searches for the best attribute upon which to split. There are various univariate criteria. These criteria can be characterized in different ways, such as according to the origin of the measure (information theory, dependence, and distance) and according to the measure structure (impurity‐based criteria, normalized impurity‐based criteria, and binary criteria). Next, we describe the most common criteria in the literature.

Figure 2.18 Top‐down algorithmic framework for decision tree induction. The inputs are S (training set), A (input feature set), and y (target feature) [8].
Impurity ‐ based criteria: Given a random variable 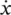 with k discrete values, distributed according to P = ( p 1, p 2, …, p k), an impurity measure is a function ϕ : [0, 1] k→ R that satisfies the following conditions: ϕ ( P ) ≥ 0; ϕ ( P ) is minimum if ∃ i such that component P i= 1; ϕ ( P ) is maximum if ∀ i , 1 ≤ i ≤ k , P i= 1/ k ; ϕ ( P ) is symmetric with respect to components of P ; φ ( P ) is differentiable everywhere in its range. If the probability vector has a component of 1 (the variable x gets only one value), then the variable is defined as pure. On the other hand, if all components are equal the level of impurity reaches a maximum. Given a training set S , the probability vector of the target attribute y is defined as
with k discrete values, distributed according to P = ( p 1, p 2, …, p k), an impurity measure is a function ϕ : [0, 1] k→ R that satisfies the following conditions: ϕ ( P ) ≥ 0; ϕ ( P ) is minimum if ∃ i such that component P i= 1; ϕ ( P ) is maximum if ∀ i , 1 ≤ i ≤ k , P i= 1/ k ; ϕ ( P ) is symmetric with respect to components of P ; φ ( P ) is differentiable everywhere in its range. If the probability vector has a component of 1 (the variable x gets only one value), then the variable is defined as pure. On the other hand, if all components are equal the level of impurity reaches a maximum. Given a training set S , the probability vector of the target attribute y is defined as
(2.12) 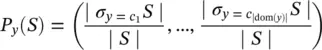
The goodness of split due to the discrete attribute a iis defined as a reduction in impurity of the target attribute after partitioning S a ccording to the values v i, j∈ dom( a i):
(2.13) 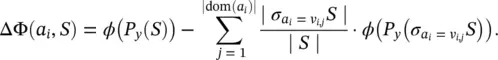
Information gain ( ig ) is an impurity‐based criterion that uses the entropy ( e ) measure (origin from information theory) as the impurity measure:

where
(2.14) 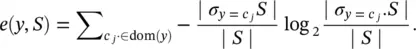
Gini index : This is an impurity‐based criterion that measures the divergence between the probability distributions of the target attribute’s values. The Gini ( G ) index is defined as
(2.15) 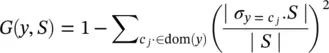
Consequently, the evaluation criterion for selecting the attribute a iis defined as the Gini gain ( GG ):
(2.16) 
Likelihood ratio chi ‐ squared statistics: The likelihood ratio ( lr ) is defined as
(2.17) 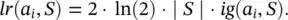
This ratio is useful for measuring the statistical significance of the information gain criteria. The zero hypothesis ( H 0) is that the input attribute and the target attribute are conditionally independent. If H 0holds, the test statistic is distributed as χ 2with degrees of freedom equal to (dom( a i) − 1) · (dom( y ) − 1).
Normalized impurity ‐ based criterion : The impurity‐based criterion described above is biased toward attributes with larger domain values. That is, it prefers input attributes with many values over attributes with less values. For instance, an input attribute that represents the national security number will probably get the highest information gain. However, adding this attribute to a decision tree will result in a poor generalized accuracy. For that reason, it is useful to “normalize” the impurity‐based measures, as described in the subsequent paragraphs.
Gain ratio ( gr ): This ratio “normalizes” the information gain ( ig ) as follows: gr ( a i, S ) = ig( a i, S )/e( a i, S ). Note that this ratio is not defined when the denominator is zero. Also, the ratio may tend to favor attributes for which the denominator is very small. Consequently, it is suggested in two stages. First, the information gain is calculated for all attributes. Then, taking into consideration only attributes that have performed at least as well as the average information gain, the attribute that has obtained the best ratio gain is selected. It has been shown that the gain ratio tends to outperform simple information gain criteria both from the accuracy aspect as well as from classifier complexity aspect.
Distance measure : Similar to the gain ratio, this measure also normalizes the impurity measure. However, the method used is different:
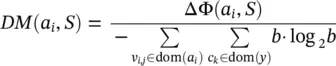
where
(2.18) 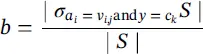
Binary criteria : These are used for creating binary decision trees. These measures are based on the division of the input attribute domain into two subdomains.
Let β ( a i, d 1, d 2, S ) denote the binary criterion value for attribute a iover sample S when d 1 and d 2 are its corresponding subdomains. The value obtained for the optimal division of the attribute domain into two mutually exclusive and exhaustive subdomains, is used for comparing attributes, namely
Читать дальше



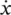 with k discrete values, distributed according to P = ( p 1, p 2, …, p k), an impurity measure is a function ϕ : [0, 1] k→ R that satisfies the following conditions: ϕ ( P ) ≥ 0; ϕ ( P ) is minimum if ∃ i such that component P i= 1; ϕ ( P ) is maximum if ∀ i , 1 ≤ i ≤ k , P i= 1/ k ; ϕ ( P ) is symmetric with respect to components of P ; φ ( P ) is differentiable everywhere in its range. If the probability vector has a component of 1 (the variable x gets only one value), then the variable is defined as pure. On the other hand, if all components are equal the level of impurity reaches a maximum. Given a training set S , the probability vector of the target attribute y is defined as
with k discrete values, distributed according to P = ( p 1, p 2, …, p k), an impurity measure is a function ϕ : [0, 1] k→ R that satisfies the following conditions: ϕ ( P ) ≥ 0; ϕ ( P ) is minimum if ∃ i such that component P i= 1; ϕ ( P ) is maximum if ∀ i , 1 ≤ i ≤ k , P i= 1/ k ; ϕ ( P ) is symmetric with respect to components of P ; φ ( P ) is differentiable everywhere in its range. If the probability vector has a component of 1 (the variable x gets only one value), then the variable is defined as pure. On the other hand, if all components are equal the level of impurity reaches a maximum. Given a training set S , the probability vector of the target attribute y is defined as