1 ...6 7 8 10 11 12 ...37 where U is the internal energy of the system and F and G are the corresponding Helmholtz and Gibbs energies defined by
 (2.55)
(2.55)
The brackets {} in ( 2.54) denote a set of state variables associated with the various species defined for k=1,…,n. The state variables S , T , V and p are the entropy, thermodynamic (i.e. absolute) temperature, volume and pressure, respectively, and the parameters μk,k=1,…,n, are the mass-based chemical potentials. Each of the relations ( 2.54) defines, for media having uniform state variables and hydrostatic stress states (i.e. in the absence of shear stresses), an equation of state for three different but equivalent selections of the independent state variables. It follows from the three differential relations in ( 2.54) that
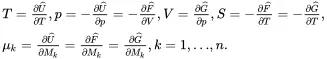 (2.56)
(2.56)
The total mass of the system denoted by M is given by
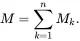 (2.57)
(2.57)
Any extensive state variable P depends directly on the total M of the system and is such that for any value of the dimensionless parameter λ
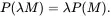 (2.58)
(2.58)
On applying this principle to the functions introduced in ( 2.54)
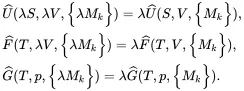 (2.59)
(2.59)
It follows that the functions U^,F^ or G^ are homogeneous of order unity in the extensive state variables. Provided that λ is independent of the state variables, on differentiating relations ( 2.59) with respect to λ, and then setting λ=1, it follows on using ( 2.56) that
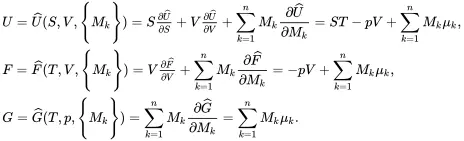 (2.60)
(2.60)
The quantities U , F , G , S , V and {Mk} are the extensive variables of uniform multi-component systems used in thermodynamics. The intensive variables, which do not depend on the total mass M of the system, are the temperature T , pressure p and the chemical potentials μk,k=1,…,n. The thermodynamic relations may only be used for uniform systems which are in a state of mechanical and thermal equilibrium. Their use needs to be extended to non-uniform states where gradients of state variables are encountered, and to dynamic states where the various species are subject to motion. In this book, diffusion mechanisms will be neglected, which means that all species at any given location in the material will move with the same velocity v.
2.9.2 Local Thermodynamic Relations
The extensive quantities are not used directly in simulations, as local expressions of these thermodynamic quantities defined per mole, per unit mass or per unit volume need to be defined. The approach to be taken here is to define thermodynamic variables per unit mass by introducing the state variables υ,ψ ,φ ,Ω and η using the relations
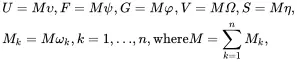 (2.61)
(2.61)
implying that
 (2.62)
(2.62)
where υ,ψ and φ are the specific internal, specific Helmholtz and specific Gibbs energies, respectively, Ω is the volume per unit mass (i.e. 1/ρ where ρ is the mass density), whereas η and ωk,k=1,…,n are, respectively, the specific entropy and mass fractions for the n species. Substitution of ( 2.61) into ( 2.54) then leads to
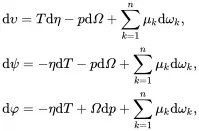 (2.63)
(2.63)
where use has been made of the following relation derived using ( 2.60) and ( 2.61)
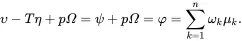 (2.64)
(2.64)
On setting λ=1/M in ( 2.59) and on using ( 2.61) the local equations of state are given by
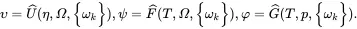 (2.65)
(2.65)
The differential relations ( 2.63) imply that
 (2.66)
(2.66)
It should be noted that the set of mass fractions {ωk} appearing as state variables in ( 2.65) are not independent because their sum is unity as shown in ( 2.61). The partial derivatives with respect to mass fractions given in ( 2.66) must, however, be calculated under the assumption that the mass fractions are independent variables but that the relationship ( 2.62) is not yet assumed to be satisfied. This means that relation ( 2.62) cannot yet be used to simplify or modify the functions U^,F^orG^. It should also be noted that the functions U^,F^andG^ appearing in the local relations ( 2.66) are, in fact, defined for uniform systems at a global level, as shown in ( 2.54) where the set of state variables {Mk}, corresponding to {ωk}, are independent. As soon as all partial derivatives with respect to mass fractions have been calculated, it is then possible to simplify or modify results by making use the mass fraction relation ( 2.62).
The description of thermodynamic relations given here applies to multi-component fluids in equilibrium, and to solids provided the stress state is hydrostatic so that shear stresses are absent. In particular, the relations apply to the uniform initial reference state of elasticity theory where the background pressure and temperature are both uniform. Although the thermodynamic relations have been given for multi-component systems, it is emphasised that this is referring to mixtures of atoms and/or molecules of the various n species, which is an example of an ‘atomistic’ composite. Throughout this book there is no need to consider materials and associated models at the atomistic length scale, as all materials are considered homogenised into macroscopic continua. The composites to be considered are formed from a continuum representing the matrix and one or more types of reinforcement which are also modelled as continua. When applying thermodynamic principles to continua, it is sufficient to regard each material present as a thermodynamic system having just a single component so that n = 1. On using ( 2.62) it is then clear that ω1=1. The equations of state ( 2.65) may then be written in the form
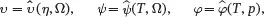 (2.67)
(2.67)
Читать дальше

 (2.55)
(2.55)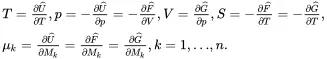 (2.56)
(2.56)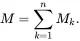 (2.57)
(2.57)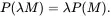 (2.58)
(2.58)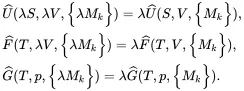 (2.59)
(2.59)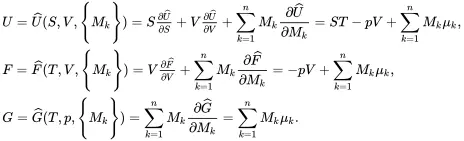 (2.60)
(2.60)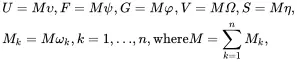 (2.61)
(2.61) (2.62)
(2.62)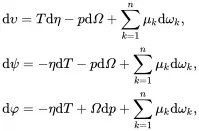 (2.63)
(2.63)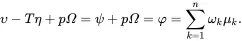 (2.64)
(2.64)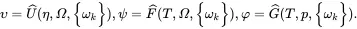 (2.65)
(2.65) (2.66)
(2.66)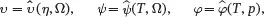 (2.67)
(2.67)










