 (2.109)
(2.109)
where vj=∂uj/∂t is the velocity vector, uj is the displacement vector and σij is the stress tensor. In the absence of body couples, the principle of the conservation of angular momentum leads to the symmetry of the stress tensor so that σij=σji.
The principle of the conservation of energy for infinitesimal deformations leads to the following local form of the internal energy balance equation that results from ( 2.44)
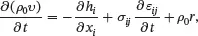 (2.110)
(2.110)
where u is the specific internal energy, hi is the heat flux vector, r is the rate (per unit mass) at which heat from non-mechanical sources may be locally generated or lost that could arise, for example, from electrical heating and εij is the infinitesimal strain tensor defined in terms of the displacement vector ui by relation ( 2.107). Relations ( 2.109) and ( 2.110) are field equations that must always be satisfied for any type of homogeneous solid that deforms as a continuous medium and is subject to infinitesimal deformations.
When developing a theory of thermoelastic materials behaviour, it is useful to introduce an equation of state of the following form (a generalisation of ( 2.67) 1to elastic materials subject to shear deformation)
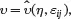 (2.111)
(2.111)
where υ^ is a prescribed function of the specific entropy η and the strain tensor εij. The corresponding differential form is written as
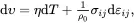 (2.112)
(2.112)
and the thermodynamic temperature T (i.e. absolute temperature, which is always positive) is then defined by the relation
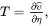 (2.113)
(2.113)
whereas the stress tensor is defined by
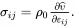 (2.114)
(2.114)
It follows from (2.110)–(2.114) that the local energy balance equation may be expressed in the form
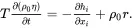 (2.115)
(2.115)
This relation is now rearranged in the form of an entropy balance equation
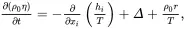 (2.116)
(2.116)
where Δ is the rate of internal entropy production per unit volume given by
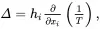 (2.117)
(2.117)
resulting from the thermodynamically irreversible process of heat conduction, and where in ( 2.116) the quantity hi/T is the entropy flux vector. In words, ( 2.116) states that the rate of change of entropy in unit volume of material is balanced by the flow of entropy through its boundary, the rate of entropy production within the material resulting from heat flow and the rate of change of entropy resulting from localised non-mechanical heating effects. The second law of thermodynamics asserts that Δ must be non-negative for all possible local states of the system. This is assured if the following heat conduction law is assumed
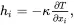 (2.118)
(2.118)
where the thermal conductivity κ≥0 can be temperature dependent. The relation ( 2.118) linearly relating the heat flux to the temperature gradient is the well-known Fourier heat conduction law that demands that heat will always flow from regions of high temperature to regions of lower temperature.
2.12 Equilibrium Equations
When a continuous medium is in mechanical equilibrium, the equations of motion ( 2.109) reduce to the form
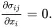 (2.119)
(2.119)
It is useful express the equilibrium equations ( 2.119) in terms of three coordinate systems that will be used later in this book. In terms of a set of Cartesian coordinates (x1,x2,x3) the equilibrium equations ( 2.119) may be expressed as the following three independent equilibrium equations (see, for example, [3])
 (2.120)
(2.120)
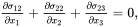 (2.121)
(2.121)
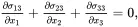 (2.122)
(2.122)
where the stress tensor is symmetric such that
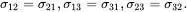 (2.123)
(2.123)
When using cylindrical polar coordinates (r,θ,z) such that
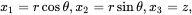 (2.124)
(2.124)
the equilibrium equations ( 2.120)–( 2.122) are written as
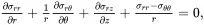 (2.125)
(2.125)
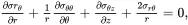 (2.126)
(2.126)
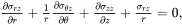 (2.127)
(2.127)
where the stress tensor is symmetric such that
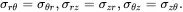 (2.128)
(2.128)
When using spherical polar coordinates (r,θ,ϕ) such that
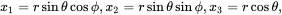 (2.129)
(2.129)
the equilibrium equations ( 2.120)–( 2.122) are written as
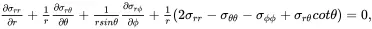 (2.130)
(2.130)
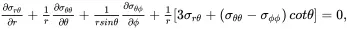 (2.131)
(2.131)
Читать дальше

 (2.109)
(2.109)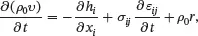 (2.110)
(2.110)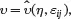 (2.111)
(2.111)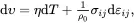 (2.112)
(2.112)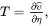 (2.113)
(2.113)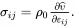 (2.114)
(2.114)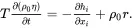 (2.115)
(2.115)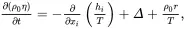 (2.116)
(2.116)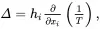 (2.117)
(2.117)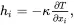 (2.118)
(2.118)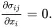 (2.119)
(2.119) (2.120)
(2.120)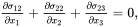 (2.121)
(2.121)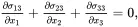 (2.122)
(2.122)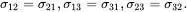 (2.123)
(2.123)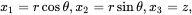 (2.124)
(2.124)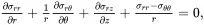 (2.125)
(2.125)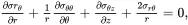 (2.126)
(2.126)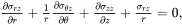 (2.127)
(2.127)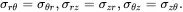 (2.128)
(2.128)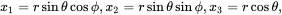 (2.129)
(2.129)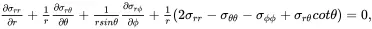 (2.130)
(2.130)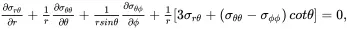 (2.131)
(2.131)










