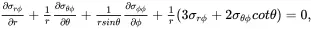 (2.132)
(2.132)
where the stress tensor is symmetric such that
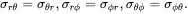 (2.133)
(2.133)
2.13 Strain–Displacement Relations
For the special case when the strain tensor εij is uniform, and on using ( 2.107), the displacement fields
 (2.134)
(2.134)
and
 (2.135)
(2.135)
both lead to the same strain field given by
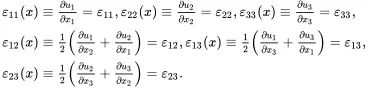 (2.136)
(2.136)
This implies that the displacement fields differ by a rigid rotation about some axis. Such a rigid rotation will not affect the values of the strain and stress fields. The form ( 2.135) for the displacement field is preferred as it is then much easier to describe the meaning of the shear strains ε12, ε13 and ε23. When ε12 is the only non-zero strain component, it follows that u1 is the only non-zero displacement component and that its value is proportional to x 2so that the shear plane is normal to the x 2-axis. Similarly, when ε13 is the only non-zero strain component, it again follows that u1 is the only non-zero displacement component and that its value is proportional to x 3so that the shear plane is normal to the x 3-axis. When ε23 is the only non-zero strain component, it follows that u2 is the only non-zero displacement component and that its value is proportional to x 3so that the shear plane is again normal to the x 3-axis.
When using cylindrical polar coordinates (r,θ,z), the displacement components ur,uθ,uz are related to the Cartesian components u1,u2,u3 as follows
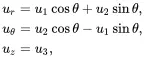 (2.137)
(2.137)
having inverse
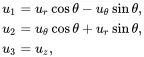 (2.138)
(2.138)
and the strain–displacement relations are given by
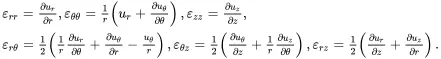 (2.139)
(2.139)
When using spherical polar coordinates (r,θ,ϕ), the displacement components ur,uθ,uϕ are related to the Cartesian components u1,u2,u3 as follows:
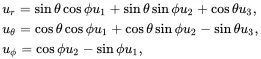 (2.140)
(2.140)
having inverse
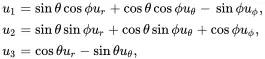 (2.141)
(2.141)
and the strain–displacement relations are given by
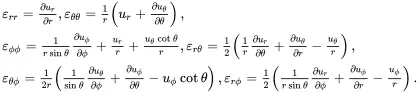 (2.142)
(2.142)
2.14 Constitutive Equations for Anisotropic Linear Thermoelastic Solids
As we are concerned in this book with various types of composite material, it is necessary to define a set of constitutive relations that will form the basis for the development of theoretical methods for predicting the behaviour of anisotropic materials. Consider a general homogeneous infinitesimal strain εkl (applied to a unit cube of the composite material) defined in terms of the displacement vector uk and the position vector xk by ( 2.107), namely,
 (2.143)
(2.143)
With the assumption that the strain field is uniform in the composite, the displacement field is linear and may be written in the form
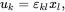 (2.144)
(2.144)
where it is assumed that the displacement vector is zero when x1=x2=x3=0.
The local equation of state ( 2.111) is not of a form that can easily be related to experimental measurements as one of the state variables is assumed to be the specific entropy η. It is much more convenient, and much more practically useful, if the state variable η is replaced by the absolute temperature T . A local equation of state for the specific Helmoltz energy is assumed to have the following form (equivalent to ( 2.111) as implied by (2.67)–(2.69))
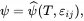 (2.145)
(2.145)
where εij is the infinitesimal strain tensor introduced in Section 2.12 (see ( 2.107)). For infinitesimal deformations, and because ψ≡υ−Tη from ( 2.64), the following differential form of ( 2.145) may be derived from ( 2.112)
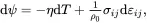 (2.146)
(2.146)
where the specific entropy η and the stress tensor σij are now defined by
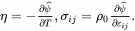 (2.147)
(2.147)
For infinitesimal deformations, a linear thermoelastic response can be assumed so that the Helmholtz energy per unit volume ρ0ψ^ has the form
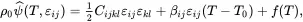 (2.148)
(2.148)
where Cijkl are the elastic constants having the dimensions of stress or modulus, βij are thermoelastic coefficients and where T0 is a reference temperature. As the strain tensor is symmetric, it follows that βij=βji and that
 (2.149)
(2.149)
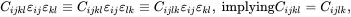 (2.150)
(2.150)
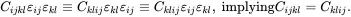 (2.151)
(2.151)
On substituting ( 2.148) into ( 2.147), it follows that
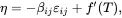 (2.152)
(2.152)
Читать дальше

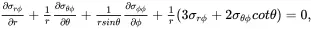 (2.132)
(2.132)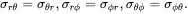 (2.133)
(2.133) (2.134)
(2.134) (2.135)
(2.135)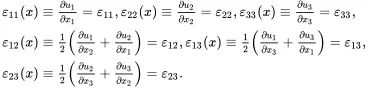 (2.136)
(2.136)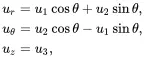 (2.137)
(2.137)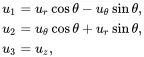 (2.138)
(2.138)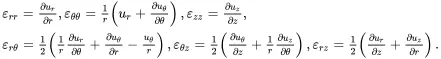 (2.139)
(2.139)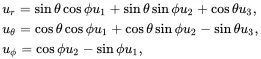 (2.140)
(2.140) (2.141)
(2.141) (2.142)
(2.142) (2.143)
(2.143) (2.144)
(2.144) (2.145)
(2.145)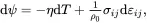 (2.146)
(2.146)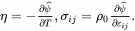 (2.147)
(2.147)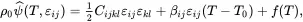 (2.148)
(2.148) (2.149)
(2.149)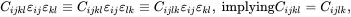 (2.150)
(2.150)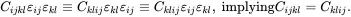 (2.151)
(2.151)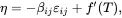 (2.152)
(2.152)










