it follows that
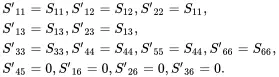 (2.190)
(2.190)
As it was assumed that S11=S22,S44=S55,S13=S23, it is clear that any rotation about the x 3-axis does not alter the value of the elastic constants on transformation. Thus, the material having the stress-strain relations ( 2.170) are transverse isotropic relative to the x 3-axis if the elastic constants are such that
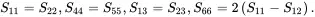 (2.191)
(2.191)
For isotropic materials, the elastic constants must satisfy the relations
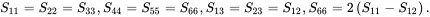 (2.192)
(2.192)
For a transverse isotropic solid the thermal expansion coefficients are such that V1=V2=V* and V3=V. It then follows from ( 2.187) that
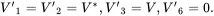 (2.193)
(2.193)
For isotropic materials
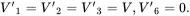 (2.194)
(2.194)
2.17.2 Introducing Familiar Thermoelastic Constants
It is useful to express the elastic constants SIJ in terms of more familiar physical quantities such as the elastic constants, for linear elastic media, known as Young’s moduli, shear moduli and Poisson’s ratios. Consider a thin rectangular plate made of an orthotropic fibre reinforced material where the in-plane directions x1 and x2 are parallel to the edges of the plate and where the through-thickness direction is parallel to the x 3-axis. The straight fibres in the plate are all parallel to the x 1-axis. For this situation, the elastic constants SIJ in ( 2.170) are written in the form
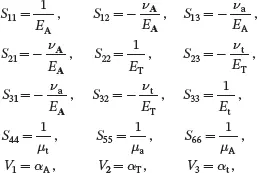 (2.195)
(2.195)
where Young’s moduli are denoted by E , shear moduli by μ, Poisson’s ratios by ν and thermal expansion coefficients by α. The stress-strain relations ( 2.170) may then be written as
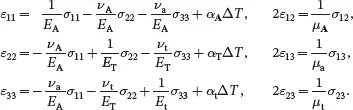 (2.196)
(2.196)
The subscripts ‘A’ and ‘T’ refer to axial and transverse thermoelastic constants, respectively, involving in-plane stresses and deformations. The subscripts ‘a’ and ‘t’ refer to axial and transverse constants, respectively, associated with out-of-plane stresses and deformations. The parameter ΔT is the difference between the current temperature of the material and the reference temperature for which all strains are zero when the sample is unloaded.
It is clear that when the plate is uniaxially loaded in the x 1-direction, the parameter νA is the Poisson’s ratio determining the in-plane transverse deformation in the x 2-direction whereas νa is Poisson’s ratio determining the transverse through-thickness deformation in the x 3-direction. When the plate is uniaxially loaded in the x 2-direction, the parameter νt is the Poisson’s ratio determining the transverse through-thickness deformation in the x 3-direction.
It is useful, first, to show the form of the stress-strain equations ( 2.196) when the material is transverse isotropic about the x 3-axis, so that they may be used when considering the properties of unidirectional plies in a laminate where the fibres are aligned in the x 3-direction of the ply, and so that use can be made of analysis given in the previous section. It follows from ( 2.196) that when the material is transverse isotropic about the x 3-axis, the stress-strain relations are of the form
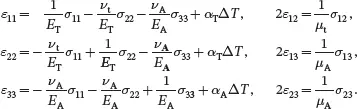 (2.197)
(2.197)
As S11=1/υT, S12=−νt/υT and S66=1/μt it follows from ( 2.189) that for a transverse isotropic solid the following condition must be satisfied:
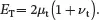 (2.198)
(2.198)
In Chapter 4considering fibre-reinforced materials, stress-strain relations are required for the cylindrical polar coordinates (r,θ,z) corresponding to the relations ( 2.197), which are given by
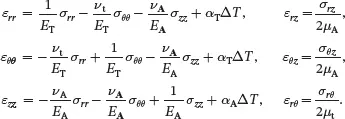 (2.199)
(2.199)
When the fibres are aligned in a direction parallel to the x 1-axis, as required in Chapters 6and 7 concerning laminates and their plies, the transverse isotropic stress-strain relations, resulting from the orthotropic form ( 2.196), are given by
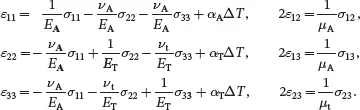 (2.200)
(2.200)
where, again, the relation ( 2.198) must be satisfied.
For plane strain conditions such that ε11≡0, it follows from ( 2.200) that
 (2.201)
(2.201)
When ΔT=0, the term ε22+ε33 is the change in volume per unit volume ΔV/V for the plane strain conditions under discussion when an equiaxial transverse stress σ is applied such that σ2=σ3=σ. It then follows that a plane strain bulk modulus kT can be defined by
 (2.202)
(2.202)
such that σ=kTΔV/V when ΔT=0.
For isotropic materials, EA=ET=E, νA=νt=ν and μA=μt=μ so that
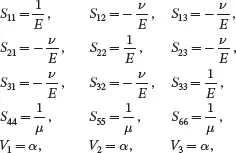 (2.203)
(2.203)
and so that ( 2.198) has the following form
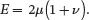 (2.204)
(2.204)
It is clear that the elastic constants of an isotropic material are fully characterised by just two independent elastic constants, such as one of the following combinations: (E,ν), (μ,ν) and (E,μ). One of Lamé’s constants λ (the other is the shear modulus μ) and the bulk modulus k are often used as elastic constants for isotropic materials. These are related to Young’s modulus E , the shear modulus μ and Poisson’s ratio ν as follows (see ( 2.161)):
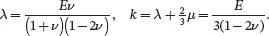 (2.205)
(2.205)
Читать дальше

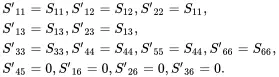 (2.190)
(2.190)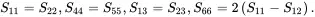 (2.191)
(2.191)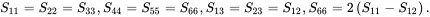 (2.192)
(2.192)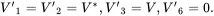 (2.193)
(2.193)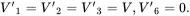 (2.194)
(2.194)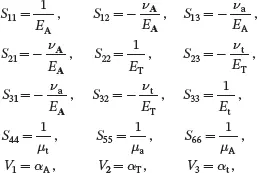 (2.195)
(2.195)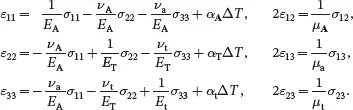 (2.196)
(2.196)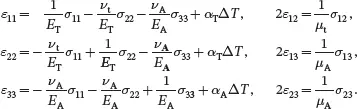 (2.197)
(2.197)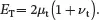 (2.198)
(2.198)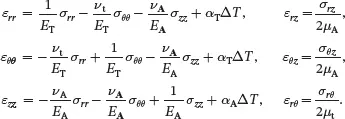 (2.199)
(2.199)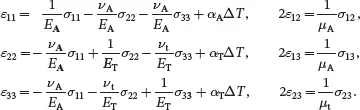 (2.200)
(2.200) (2.201)
(2.201) (2.202)
(2.202)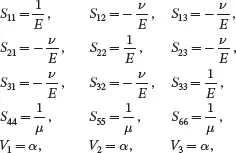 (2.203)
(2.203)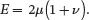 (2.204)
(2.204)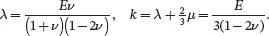 (2.205)
(2.205)










