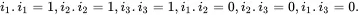 (2.1)
(2.1)
The three coordinates (x1,x2,x3) describe the location of a point xthat is known as the position vector, which may be written as x=x1i1+x2i2+x3i3. In tensor theory based on Cartesian coordinates, this is written in the shorter form x=xkik where a summation over values k = 1, 2, 3 is implied when a suffix is repeated ( k in this example). Any vector v may be written as v=v1i1+v2i2+v3i3, or as v=vkik when using tensor notation. The scalar quantities vk, k = 1, 2, 3, are the components of the vector v with values depending on the choice of coordinates. The magnitude of the vector v is specified by
 (2.2)
(2.2)
and its value is independent of the system of coordinates that is selected. The magnitude is, thus, an invariant of the vector.
The unit vector in the direction of the vector v is specified by v/|v|. Examples of vectors that occur in the physical world are forces, displacements, velocities and tractions.
The tensors to be used in the book are either second order or fourth order. Tensors are usually physical quantities that are independent of the coordinate system that is used to describe their properties. For the given coordinate system having unit vectors i1, i2and i3, a second-order tensor tis expressed in terms of the unit vectors as follows:
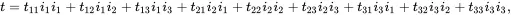 (2.3)
(2.3)
or, more compactly, using tensor notation in the form
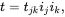 (2.4)
(2.4)
where summation over values 1, 2, 3 is implied by the repeated suffices j and k . The quantities tjk are known as the components of a second-order tensor with values depending on the choice of coordinates. There are three independent invariants of second-order tensors which can be expressed in a variety of forms, the simplest being
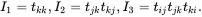 (2.5)
(2.5)
A fourth-order tensor Tis expressed in terms of the unit vectors of the coordinate system as follows
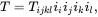 (2.6)
(2.6)
where summation over values 1, 2, 3, is implied by the repeated suffices i , j , k and l . The quantities Tijkl are known as the components of a fourth-order tensor with values depending on the choice of coordinates.
2.3.1 Fourth-order Elasticity Tensors
Elastic stress-strain equations are often written in the following form (see, for example, ( 2.153) and ( 2.154) given later in the chapter which includes thermal terms).
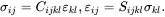 (2.7)
(2.7)
It is clear that
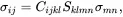 (2.8)
(2.8)
which may be written as
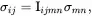 (2.9)
(2.9)
where
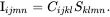 (2.10)
(2.10)
The fourth-order tensor Iijmn can be defined by
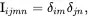 (2.11)
(2.11)
where δij denotes the Kronecker delta symbol which has the value unity when i = j and the value zero otherwise. Clearly
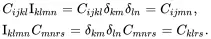 (2.12)
(2.12)
The identity tensor defined by ( 2.11) does not exhibit the same symmetry as the stiffness and compliance tensors, which are such that
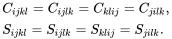 (2.13)
(2.13)
It is noted that
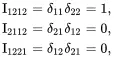 (2.14)
(2.14)
indicating that Iijmn≠Ijimn and Iijmn≠Ijinm.
A symmetric fourth-order identity tensor may be defined by
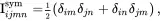 (2.15)
(2.15)
so that
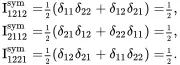 (2.16)
(2.16)
The definition ( 2.15) is used to define the fourth-order identity tensors used in this book which are denoted by I or I.
2.4 Displacement and Velocity Vectors
Consider a continuous elastic medium that is being deformed from some homogeneous initial state as a result of loading. At some time t , a material point at xwill have moved from its initial location x¯ in the material. The motion of the medium can be described by the following transformation gand its inverse G
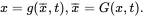 (2.17)
(2.17)
The vector x¯ defines ‘material coordinates’, associated with the motion of the medium that, together with the function g, can be used to describe the spatial variation during deformation of any physical quantity with respect to its original configuration. The transformation ( 2.17) is assumed to be single-valued and possess continuous partial derivatives with respect to their arguments. It is also assumed that the inverse function Gexists locally, and this is always the case when the Jacobian J is such that
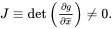 (2.18)
(2.18)
The displacement of a material point x¯ is denoted by u(x¯,t) when using material coordinates, and is defined by
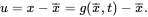 (2.19)
(2.19)
Читать дальше

 (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3)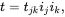 (2.4)
(2.4)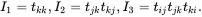 (2.5)
(2.5)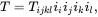 (2.6)
(2.6)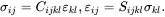 (2.7)
(2.7)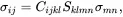 (2.8)
(2.8)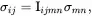 (2.9)
(2.9)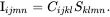 (2.10)
(2.10)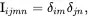 (2.11)
(2.11)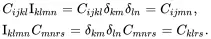 (2.12)
(2.12)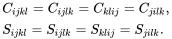 (2.13)
(2.13)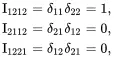 (2.14)
(2.14)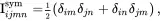 (2.15)
(2.15)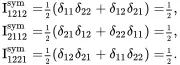 (2.16)
(2.16)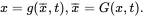 (2.17)
(2.17)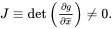 (2.18)
(2.18)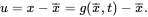 (2.19)
(2.19)










