The velocity vof a material point x¯ may be calculated using the relation
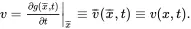 (2.20)
(2.20)
2.5 Material Time Derivative
The concept of a material time derivative (often named the substantive derivative) associated with the motion of the material is fundamental to the mechanics of continuous media. If ϕ is any scalar, vector or tensor quantity such that ϕ(x,t)≡ϕ¯(x¯,t), then its material time derivative is defined by
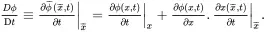 (2.21)
(2.21)
On using ( 2.20) the material time derivative may then be written as
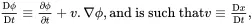 (2.22)
(2.22)
where ∇ denotes the gradient with respect to the coordinates x.
Consider now a region V of the system bounded by the closed surface S enclosing a sample of the medium which is moving such that the velocity distribution at time t is denoted by v(x,t). It follows that, for any extensive property ϕ(x,t) of the system, the material time derivative (associated with the mean motion) of the integral of ϕ(x,t) over the region fixed region V may be written as
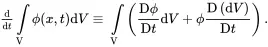 (2.23)
(2.23)
From reference [1, Equation (2.4.9)], for example,
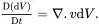 (2.24)
(2.24)
On substituting ( 2.24) into ( 2.23) it follows on using ( 2.22) that
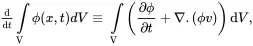 (2.25)
(2.25)
where use has been made of the following identity
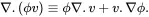 (2.26)
(2.26)
On using the divergence theorem, the identity ( 2.25) may then be written as
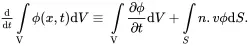 (2.27)
(2.27)
The first term on the right-hand side accounts for any changes of the property ϕ locally at points within the region V , whereas the second term accounts for the mean advection of the property across the bounding surface S where n is the outward unit normal to the surface S bounding the region V. The important identities ( 2.22) and ( 2.27) are used repeatedly in the following analysis.
Consider at time t a moving sample of material occupying a fixed volume V bounded by a closed surface S . In the absence of mass source and sink terms, the total mass of material within the region V is fixed so that on setting ϕ = ρ in (2.27) the global form of the mass balance equation for the medium may be written as
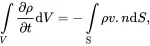 (2.28)
(2.28)
where ρ is the mass density. The term on the left-hand side of ( 2.28) is the rate of change of the total mass in the fixed region V . The term on the right-hand side is the rate at which the mass of the medium is transported across the surface S into the region V . On using the divergence theorem, the mass balance equation may be written as
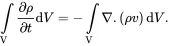 (2.29)
(2.29)
As ( 2.29) must be valid for any region V of the system, the following local form of the mass balance equation for the medium must be satisfied at all points in the system for all times t
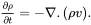 (2.30)
(2.30)
On using ( 2.22) and the identity ( 2.26), the continuity equation ( 2.30) may be written in the equivalent form
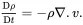 (2.31)
(2.31)
2.7 Equations of Motion and Equilibrium
The global form of the linear momentum balance equation for a fixed region V bounded by the closed surface S having outward unit normal nis written as
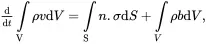 (2.32)
(2.32)
where σ is the stress tensor and where bis the body force per unit mass acting on the medium. Such body forces usually arise from the effects of gravity. On using ( 2.27) and the divergence theorem, the linear momentum balance equation ( 2.32) may be written as
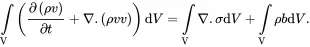 (2.33)
(2.33)
As relation ( 2.33) must be satisfied for any region V of the system, it follows that the local form of the linear momentum balance equation has the form
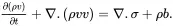 (2.34)
(2.34)
As
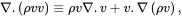 (2.35)
(2.35)
it follows from ( 2.34) on using ( 2.22) that
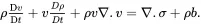 (2.36)
(2.36)
On using ( 2.31), relation ( 2.36) reduces to the well-known equation of motion
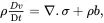 (2.37)
(2.37)
which must be satisfied at every point in the medium for all times t > 0.
It is worth noting that by considering the balance of angular momentum it can be shown that in the absence of couple stresses, the stress tensor σ must be symmetric.
2.8 Energy Balance Equation
The energy balance equation is derived from the first law of thermodynamics which requires that, for a fixed region V bounded by a closed surface S , the rate of change of the sum of the internal energy and kinetic energy is balanced by the sum of the heat flowing across the external surface S , and the rate of working of the external tractions acting on S and of the body force acting in V . There are two types of stored energy that must be considered. The first is the internal energy that accounts for the strain energy stored owing to elastic deformation and the energy of the thermal agitations of atoms in the solid. The second is the kinetic energy arising from the local average motion of the medium. In addition, the heat flow across the external boundary and the mechanical work done by the applied tractions must be considered. Body forces such as that caused by gravity also need to be taken into account. A final type of energy is the local heating that can arise, for example, from the flow of electric currents when electrodynamic effects are otherwise neglected. However, this local heating term is a very useful theoretical device for imposing precise isothermal conditions in a simulation. Owing to various energy dissipation processes, heat will be generated locally in the medium, leading to temperature variations and heat flow. Imagine that it is possible to add or remove heat at every point of the medium, and that this may be controlled to maintain a constant uniform temperature at all points. This approach to achieving isothermal conditions requires the use of a distribution of local heat sources or sinks. An alternative method is to impose isothermal conditions only on the external boundary, and to assume that the thermal conductivity is effectively infinite so that the heat generated within the medium by dissipation processes can flow immediately out of the system, thus maintaining a uniform temperature.
Читать дальше

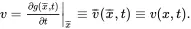 (2.20)
(2.20)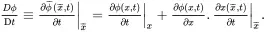 (2.21)
(2.21)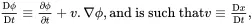 (2.22)
(2.22)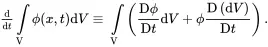 (2.23)
(2.23)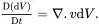 (2.24)
(2.24)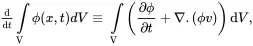 (2.25)
(2.25)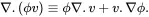 (2.26)
(2.26)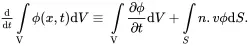 (2.27)
(2.27)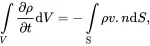 (2.28)
(2.28)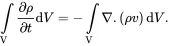 (2.29)
(2.29)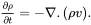 (2.30)
(2.30)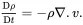 (2.31)
(2.31)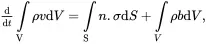 (2.32)
(2.32)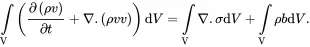 (2.33)
(2.33)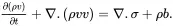 (2.34)
(2.34)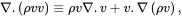 (2.35)
(2.35)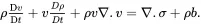 (2.36)
(2.36)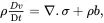 (2.37)
(2.37)










