In the absence of electrodynamic effects, the global form of the energy balance equation is written as
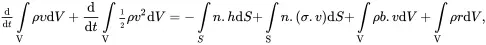 (2.38)
(2.38)
where υ is the specific internal energy, his the heat flux vector and r is a local rate of heat supply per unit mass. In ( 2.38), the symbol v 2is used to denote the value of the scalar product v. v. On using ( 2.27) the energy balance equation ( 2.38) may be written as
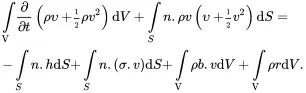 (2.39)
(2.39)
On using the divergence theorem, it then follows that
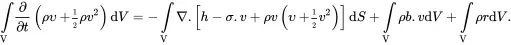 (2.40)
(2.40)
As relation ( 2.40) must be satisfied for all regions V , this leads to the following local form for the energy balance equation
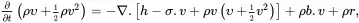 (2.41)
(2.41)
which must be satisfied at every point in the medium for all times t > 0. On using the continuity equation ( 2.30), the local energy balance equation reduces to the form
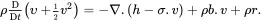 (2.42)
(2.42)
From the equation of motion ( 2.37) it follows, on taking the scalar product with the velocity vector v, that
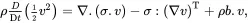 (2.43)
(2.43)
where a superscript T denotes that the transpose of the tensor must be used. The symbol: is defined here such that for any second-order tensors aand bthe double scalar product a:b≡aijbji. An alternative definition a:b≡aijbij is sometimes used in the literature. On using ( 2.43), together with the symmetry of the stress tensor, ( 2.42) reduces to the form
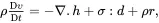 (2.44)
(2.44)
where dis the symmetric rate of deformation tensor defined by
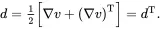 (2.45)
(2.45)
Relation ( 2.44) is the well-known local form of the internal energy balance equation for a continuous medium.
2.8.1 Conservative Body Forces
Consider now the special case when the heat source per unit mass r = 0 and the body force is derivable from a scalar potential function ζ as follows
 (2.46)
(2.46)
The effects of the Earth’s gravitational field can then be taken into account. The substitution of ( 2.46) into ( 2.41) leads to the relation
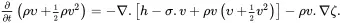 (2.47)
(2.47)
As
 (2.48)
(2.48)
it then follows from ( 2.47) that the local form ( 2.44) for the total energy balance equation may also be expressed
 (2.49)
(2.49)
The energy balance equation may, therefore, be written in the more compact form
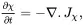 (2.50)
(2.50)
where the total energy per unit volume χ is given by
 (2.51)
(2.51)
which is the sum of the internal energy, potential energy and kinetic energy per unit volume, and where the total energy flux Jχ is given by
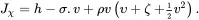 (2.52)
(2.52)
On using ( 2.51), relation ( 2.52) may also be written in the form
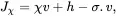 (2.53)
(2.53)
which identifies the mechanisms whereby energy can enter or leave the system, namely advection (the term χv), as heat (the term h) and as external work (the term −σ.v).
The energy balance equation ( 2.50) implies energy conservation as the energy within any region V always remains fixed during any nonequilibrium process provided that there is no energy flow across the surface S bounding the region V . This result is easily established by integrating ( 2.50) over the region V , and then making use of the divergence theorem.
2.9 Equations of State for Hydrostatic Stress States
The balance equations of mass, momentum and energy introduce a variety of physical variables, but they do not involve in any way the properties of materials. An equation of state must now be introduced, implying the existence of a variety of material properties, depending upon the complexity of the material. If elastic effects are to be included in models, then it is through an equation of state that they must be introduced. Before using strain as a thermodynamic state variable, it is useful first to introduce some key thermodynamic relationships that can be applied when the stress field is hydrostatic, i.e. shear stresses are absent, characterised by a pressure p , such that the stress tensor has the form σ=−pI where Iis the second-order unit tensor.
2.9.1 Global Thermodynamic Relations
It is essential to understand fully the nature of thermodynamic principles that underpin modelling procedures. It is assumed now that the system studied is multi-component and uniform, and that the temperature and pressure are uniform as would be the case for many equilibrium states of the system. At equilibrium, the classical thermodynamic relations for a uniform multi-component mixture, where Mk,k=1,…,n denote the total masses of the various species, are given by
 (2.54)
(2.54)
Читать дальше

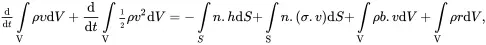 (2.38)
(2.38)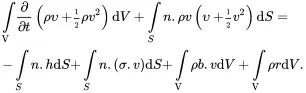 (2.39)
(2.39)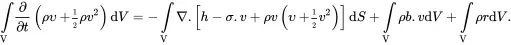 (2.40)
(2.40)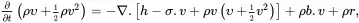 (2.41)
(2.41)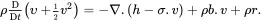 (2.42)
(2.42)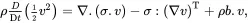 (2.43)
(2.43)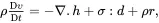 (2.44)
(2.44)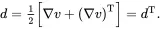 (2.45)
(2.45) (2.46)
(2.46)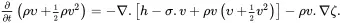 (2.47)
(2.47) (2.48)
(2.48) (2.49)
(2.49)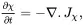 (2.50)
(2.50) (2.51)
(2.51)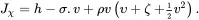 (2.52)
(2.52)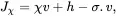 (2.53)
(2.53) (2.54)
(2.54)










