Петр Путенихин - Правила счета элементов бесконечного множества

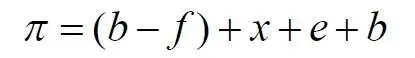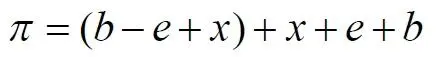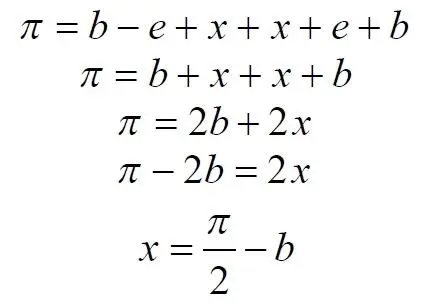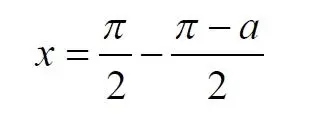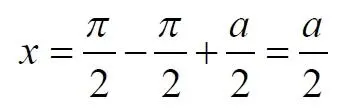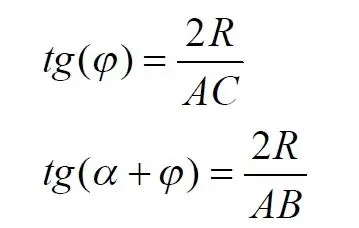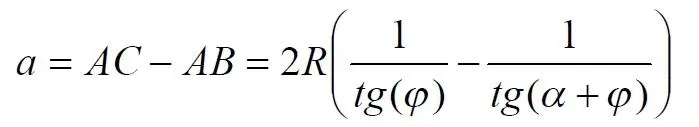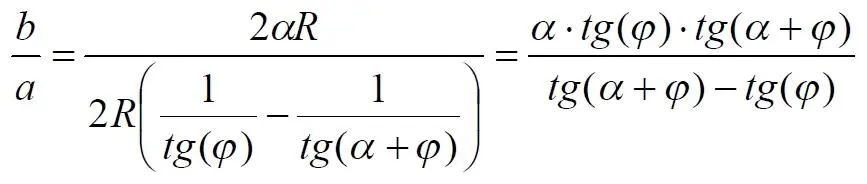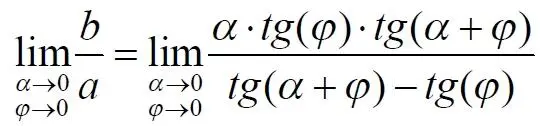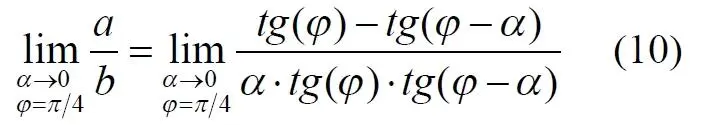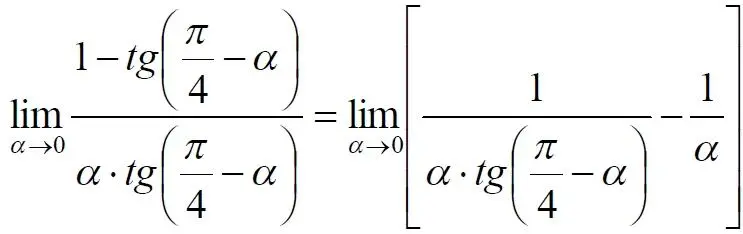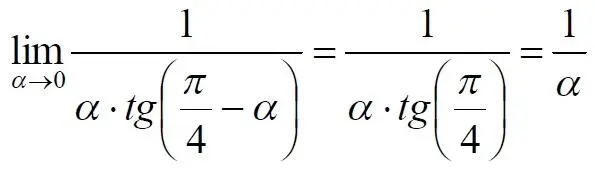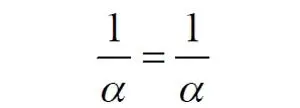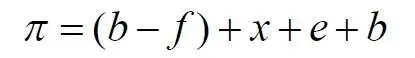
Подставляем условно известное значение угла f:

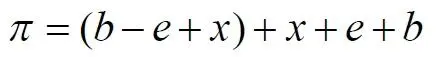
Раскрываем скобки

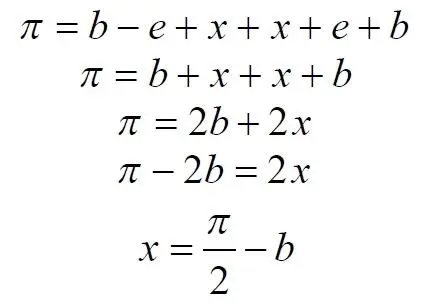
Подставляем значение заданного угла а

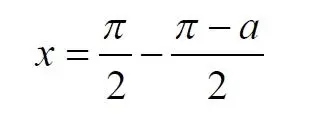
Упрощаем выражение

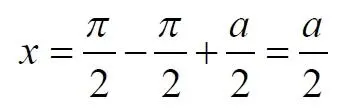
Что и требовалось доказать.

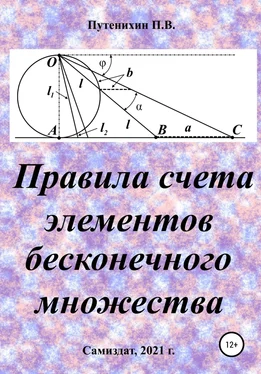
Согласно этой теореме, на рис.3 длина дуги окружности в пределах угла α равна 2αR, поскольку угловая величина дуги равна 2α. Длину линии проекции a в основании проекционного угла найдем как разницу сторон двух прямоугольных треугольников:

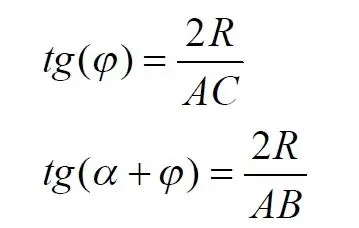
Отсюда находим величину а :

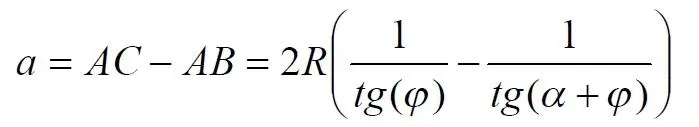
Как и выше, найдем отношение длины отсекаемой на окружности дуги к длине этого отрезка:

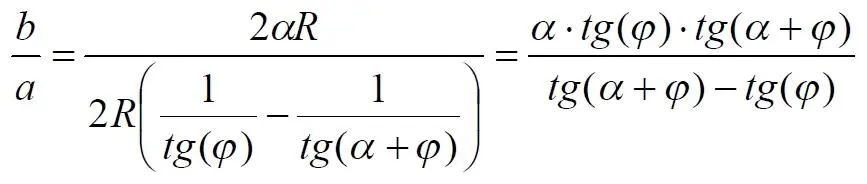
Найдем предел этой величины, когда каждый из углов стремится к нулю. В этом случае обе проекционные линии сблизятся до слияния, а их средняя линия будет стремиться к горизонтальному положению:

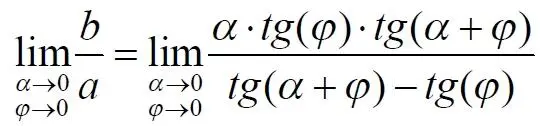
В общем случае мы получаем неопределенность, поскольку к нулю стремятся и числитель и знаменатель. Поэтому мы поступим следующим образом. Найдем эти пределы для нескольких конкретных значений среднего проекционного угла φ. В этом случае неопределенность не устраняется, но мы табличным методом построим соответствующие графики, которые визуально продемонстрируют наличие конечных пределов. Табличные значения сходятся удовлетворительно быстро, поэтому в пределах точности приложения Excel были получены следующие значения пределов для произвольно взятых значений угла φ:

Как видим, пределы существуют для любого значения проецирующей линии, угла проецирования. Поскольку вычисление предела функции неочевидно, приведём геометрический способ его вычисления для частного значения угла, рассмотренного на рис.3, значение которого определяется из геометрических соображений и равно 45 о. Увеличим до бесконечности масштаб фрагмента рисунка в точке пересечения проецирующей прямой и окружности:

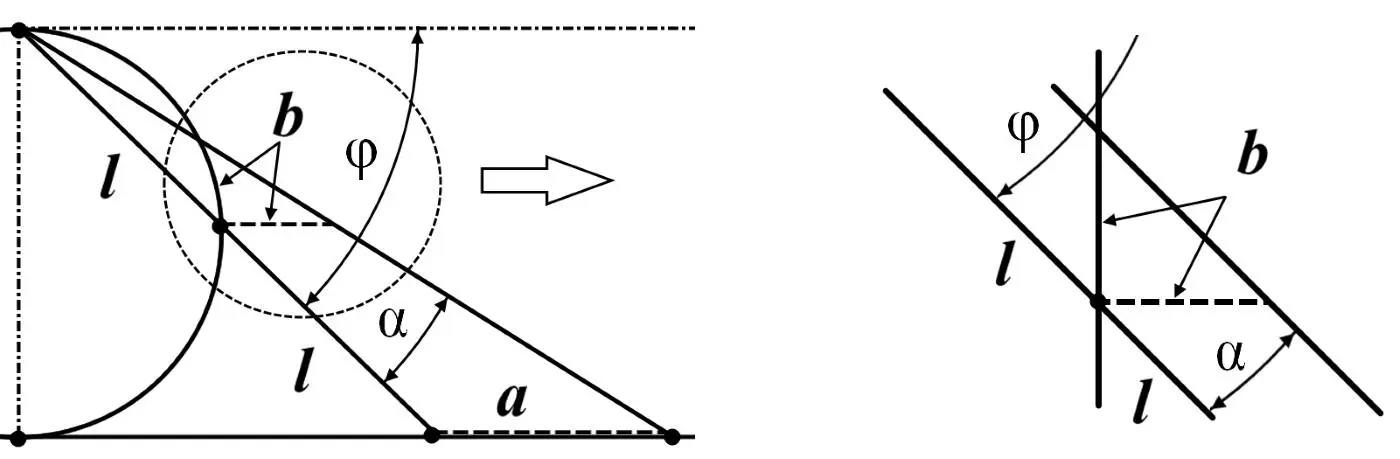
Рис.5. Увеличенный фрагмент рисунка 3

На рисунке угол φ =45 о, а угол α→0. Как видим на рисунке, фрагмент проецируемой окружности выглядит вертикальной прямой, а две проецирующие прямые – параллельны. Следовательно, отрезки b – на окружности и параллельный проецирующей плоскости оказываются перпендикулярными и образуют равносторонний прямоугольный треугольник. Отсюда и следует значение предела lim = 0,5 в третьей строке таблицы пределов и в выражении (9). Очевидно, что геометрическое вычисление предела несложно сделать и для других углов проецирующего луча. Напротив, определить это значение аналитически, вычислением предела выражения:

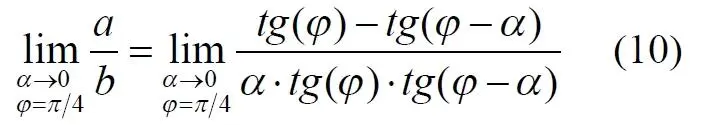
довольно сложно. Подставим значение угла φ

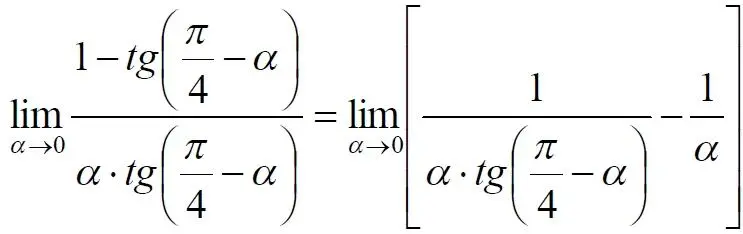
Как видим, под знаком предела находится разность двух бесконечно больших величин, причем это не просто равномощные бесконечности, они тождественны. Действительно, в пределе α→0 мы имеем:

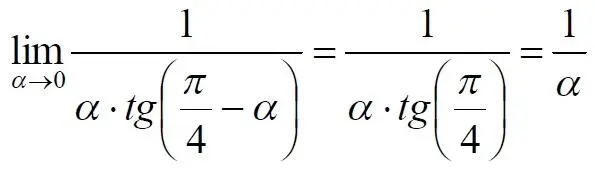
Что и можно записать как тождество

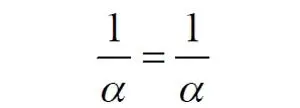
Это довольно интересное обстоятельство: две бесконечности равны, однако, тем не менее, дают разность 2. В общем-то, это свойство не уникально. Его легко показать на другом примере: n +2 = n, если n→∞. Здесь также две равные бесконечности, но при вычитании одной из другой мы получаем конечное число. Значение предела (10) нам известно, он равен 2, то есть при α→0 мы имеем