Петр Путенихин - Правила счета элементов бесконечного множества

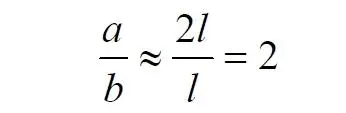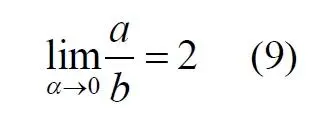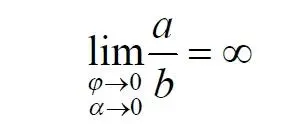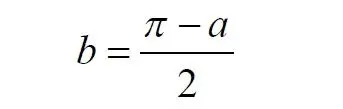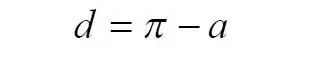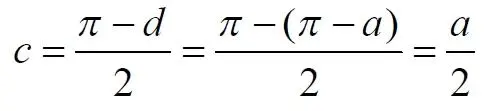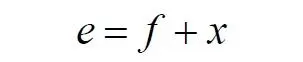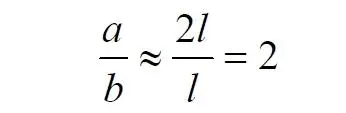
Здесь знак неточного равенства взят из предположения, что отрезок b приблизительно равен длине дуги. Это не точное равенство, но в средней части окружности отрезок и дуга отличаются друг от друга незначительно, в конечное число раз. Теперь найдем предел этого отношения, когда угол между двумя проецирующими прямыми стремится к нулю:

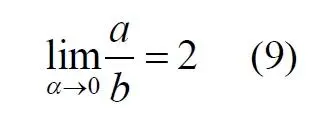
Это очевидный и аналитически достоверный предел. Но при этом возникает вопрос: что же означает это отношение 2? Две проекционные прямые слились в одну, и эта прямая пересекает и окружность и плоскость в одной точке каждую. Что же означает это соотношение для двух разных точек? Если считать, что точка – это то, что не имеет частей, то ответ становится совершенно туманным. Выходит, что точки не имеют частей, но в разном количестве. В любом случае для утверждения, что точка на окружности спроектировалась в единственную тождественную точку на плоскости, четких, бесспорных оснований уже нет.

Однако это соотношение мы нашли для конкретного, среднего угла. А что если пару прямых, проектирующих лучей повернуть ближе к горизонтальному направлению? То есть, устремить к нулю не только угол между проецирующими прямыми, но и их средний угол к плоскости. В этом случае мы увидим, что отношение будет стремиться к бесконечности:

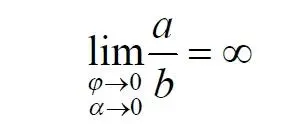
Вопрос о смысле этого отношения становится еще более острым. Если две точки – исходная, проецируемая и её проекция – отождествляются, тогда что означает это отношение? Изначально оно составлялось как отношение длины проецируемого отрезка и проекции, которые в дальнейшем уменьшением угла до нуля были преобразованы в точки. Хотя точка и не имеет частей, но величина соотношения определенно выглядит как количество проецируемых точек в проекции. Звучит весьма странно: проецирующий луч создаёт проекцию, имеющую явно не нулевые, не точечные размеры. Можно сколько угодно с этим не соглашаться, но как можно иначе рационально объяснить это соотношение?

Обычно бесконечно малые величины в алгебре характеризуются параметром порядка малости. Если две величины имею отношение конечной величины, то они считаются величинами одного порядка малости. Если отношение стремится к бесконечности, то величины имеют разный порядок малости. С учетом этого следует предположить, что стереографическая проекция окружности на плоскость некорректна, а проекциями её точек фактически являются плоские фигуры, отрезки.

Рассмотрим эту же ситуацию с другой точки зрения, не отождествляя дугу окружности и прямой отрезок. Для этого нам понадобится следующее интересное соотношение, теорема. Если к отрезку дуги провести по два луча из центра окружности (рис.4) и из любой точки окружности, кроме точек этой дуги, то угол между лучами в первом случае будет в два раза больше угла между лучами во втором случае. Приведем краткое доказательство этой теоремы.

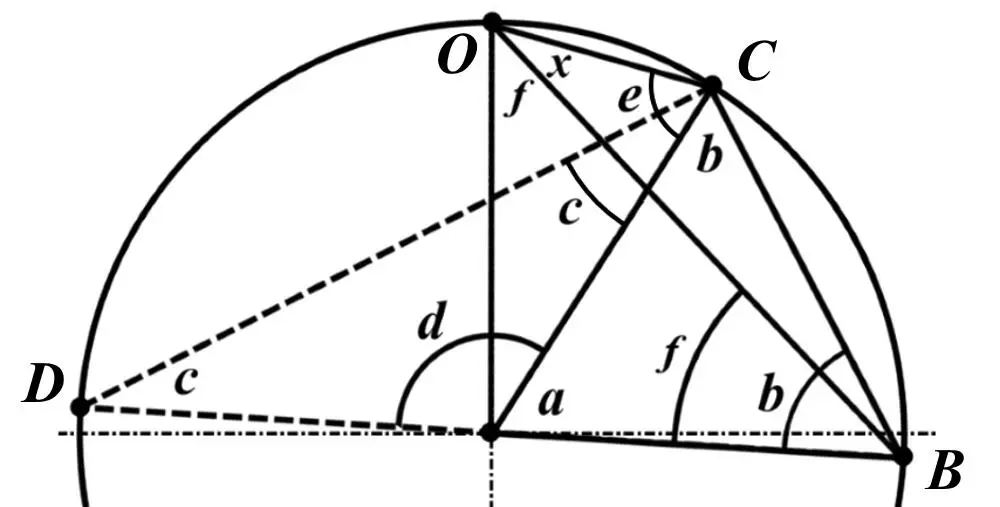
Рис.4. Теорема об углах на дуге окружности

Итак, возьмем на окружности рис.4 некоторую произвольную дугу CB и проведем к ней две пары лучей – из центра и из полюса О. Проведем далее вспомогательный диаметр BD и линию CD. Обозначим одинаковыми буквами равные углы в равносторонних треугольниках у равных сторон. По условиям задачи нам задан некий центральный угол a. Докажем, что а = 2x. Из построений на рисунке видим:

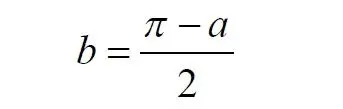
Угол при вершине штрихового треугольника:

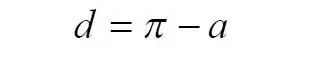
Углы при основании равностороннего треугольника.

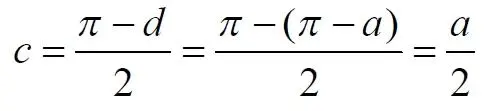
Углы при основании равностороннего треугольника с искомым углом:

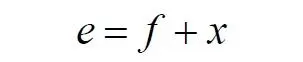
Составляем баланс углов в треугольнике с искомым углом x: