Петр Путенихин - Правила счета элементов бесконечного множества

Описать этот процесс однозначно и максимально развернуто крайне сложно. Поэтому рассмотрим ещё один пример. Пусть отрезок [0, 1] состоит из миллиарда (10 9) точек, а соответствующий ему квадрат, следовательно, содержит 10 18точек. Эти числа являются так же и количествами их порядковых номеров, эквивалентами мощностей этих множеств. Сразу же обнаруживаем, что на линии точек меньше, чем в квадрате. Если постоянно удваивать количество точек вплоть до бесконечности, это отношение будет только возрастать.

Если для отождествления мы возьмём произвольную точку указанного квадрата, то её координатный индекс будет содержать 10 18знаков после запятой. И мы не имеем никакого права отождествлять этот индекс с точкой на линии, поскольку на ней допустимы только числа с 10 9знаков после запятой, точек с такой дискретностью на линии просто нет. При увеличении дискретности квадрата и линии это расхождение будет расти по квадратичному закону.

Кстати, здесь мы наглядно обнаруживаем абсурдность сравнивания количества чисел натурального ряда и его части. Мы можем диагональным процессом Кантора тривиально перенумеровать точки линии и точки квадрата, даже не формируя для них индексы, и получим при этом равенство их количества. Однако мы только что увидели, что такое равенство противоречиво, а попросту его нет. Следовательно, и сравнивание количества членов множеств путем их раздельного пересчитывания – это опасный, ошибочный, некорректный метод, позволяющий получить любой желаемый результат, и которым следует пользоваться предельно продуманно.

Действительно, мы можем сравнивать точки линии и точки квадрата таким же простым раздельным пересчетом, получив в обоих случаях бесконечность . Но это разные бесконечности, бесконечности разной мощности. Напротив, возьмем какую-либо y -линию на квадрате и начнем пересчитывать на ней точки: 1, 2, 3 и так далее. Одновременно с этими точками будем пересчитывать и точки на линии: 1, 2, 3 и так далее. Мы тем самым однозначно отождествим все точки линии со всеми точками на одной из линий квадрата. Остальные линии квадрата, с другими координатами, разумеется, останутся без номеров. Это самый правильный способ пересчета и отождествления.

Итак, даже при ослаблении нашей аргументации мы приходим к выводу, который противоречит выводу Кантора об их равенстве. Два способа нумерации, основанных тождественно на одном и том же методе, приводят к несовместимым, противоположным выводам. Поэтому этот метод Кантора логически неверен, ошибочен. И вновь возникает риторический вопрос, какой же в этом случае метод верный? Методов группировки может быть сколько угодно, поэтому верным является только один метод – без группировки, то есть, сравнивать можно только равнозначные объекты – линию с линией. В этом случае вывод однозначный – множества точек линии и квадрата не равномощны. Самым простым и наглядным способом определения этого является простое наложение линии на квадрат и отождествление соприкоснувшихся точек.

Практически такая же противоречивая ситуация возникает и при отождествлении двух противоположных сторон квадрата: верхней и нижней, либо любых двух средних линий квадрата. Возникает совершенно противоестественная ситуации: эти пары линий вообще нельзя отождествить, поскольку нумерация их точек не имеет одинаковых значений. Верхняя сторона квадрата должна иметь по Кантору значения первой цифры после запятой всех точек, начинающиеся с 9, а нижняя – с 0, а средние, например, с 3 и 5. Две явно одинаковые линии оказываются несопоставимыми.

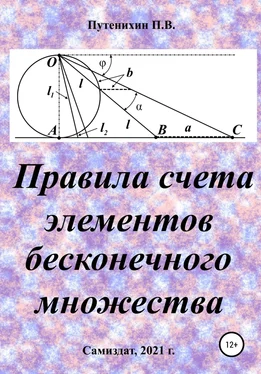
В заключение отметим, что один из истоков или примеров отождествления бесконечностей разной мощности можно обнаружить в механизме стереографической проекции, также фактически отождествляющей точку и отрезок. Рассмотрим соотношение между размерами двух отрезков, которые затем сожмем в точки:

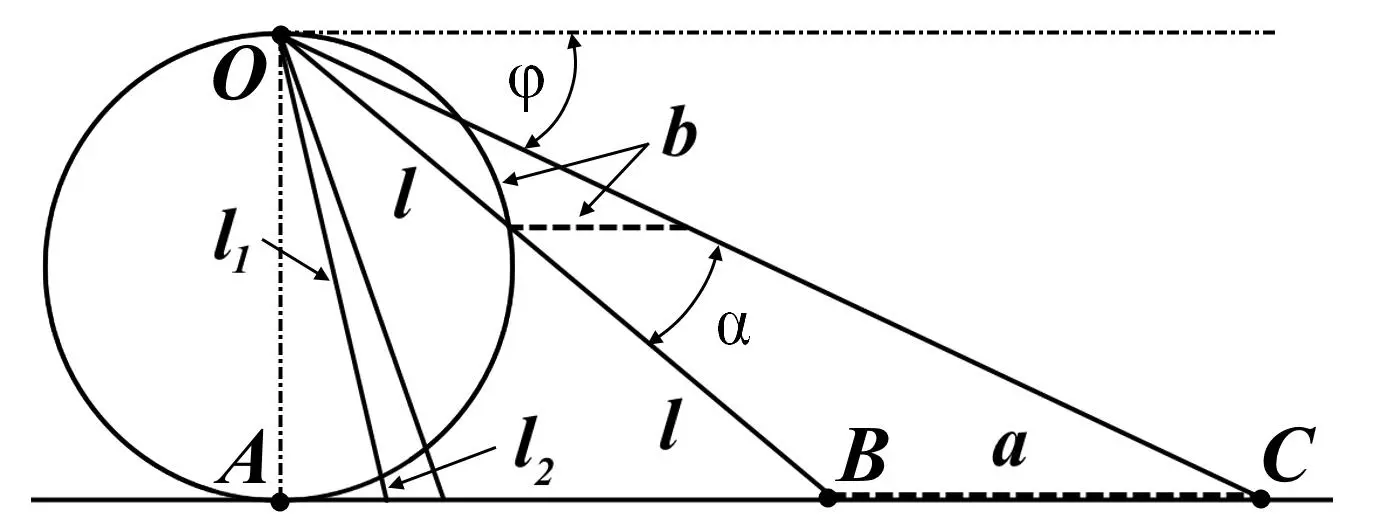
Рис.3. Стереографическая проекция отождествляет отрезок и точку

Мы не описываем сущность стереографической проекции, её описание можно найти в литературе. Каждая проекционная линия, прямая делится проецируемой точкой окружности между полюсом и проекционной плоскостью на две части, например, l 1и l 2. Возьмем частный случай, когда отрезок делится пополам, то есть, l 1= l 2= l . Проведем ещё одну проекционную линию под углом α к исходной линии. В этом случае на окружности образуется дуга, а на плоскости – отрезок. Проведем из проецируемой точки пересечения дополнительный отрезок между проекционными лучами параллельно плоскости из проецируемой точки. Обозначим полученный отрезок через b , а проекцию на плоскости – через a . Из подобия треугольников следует, что