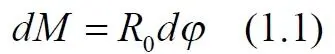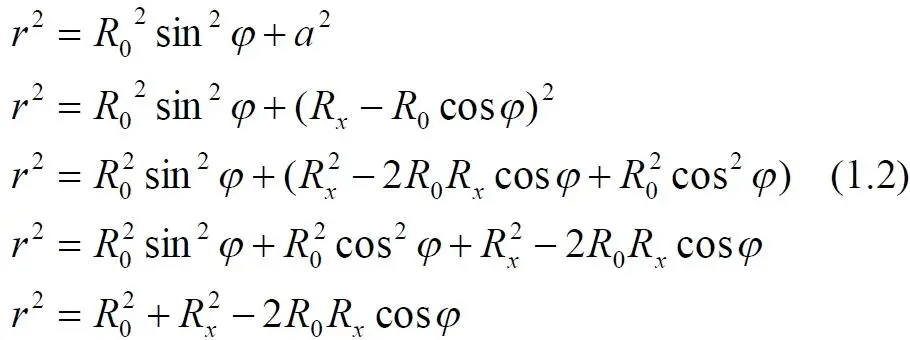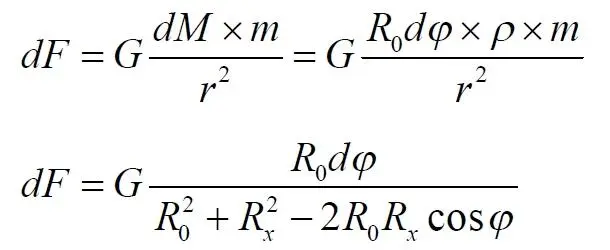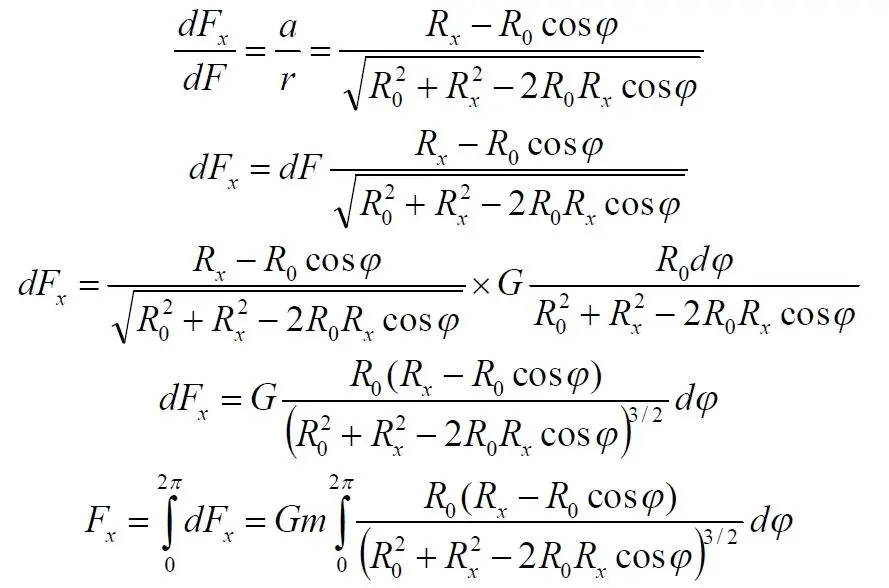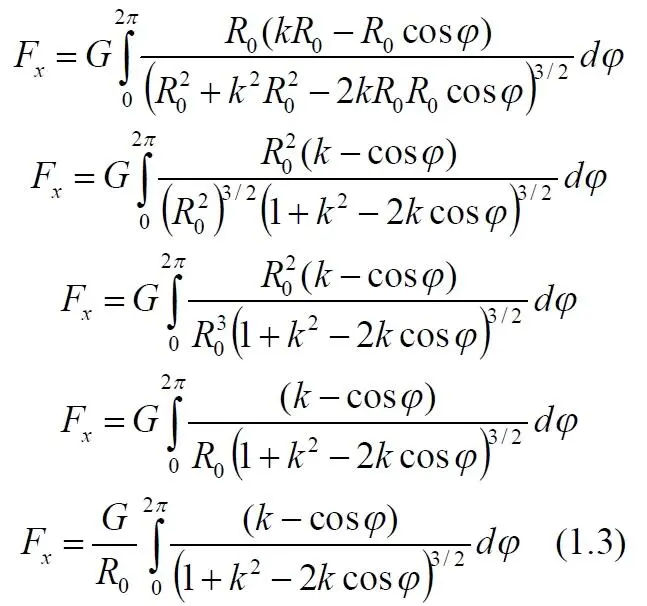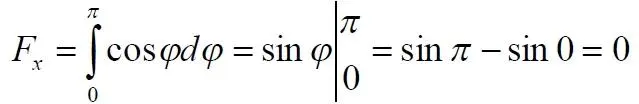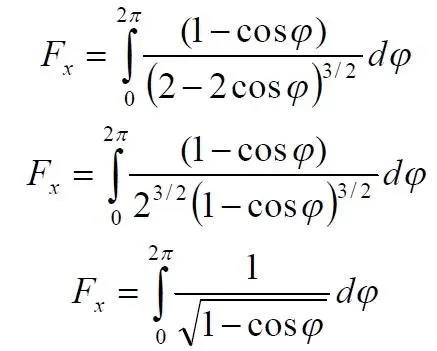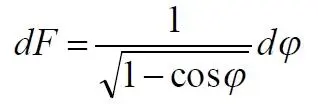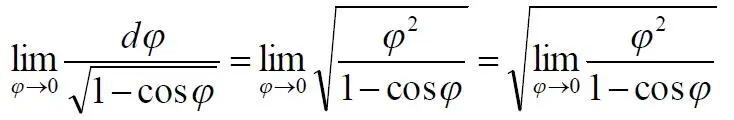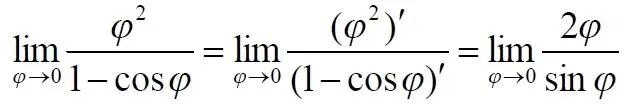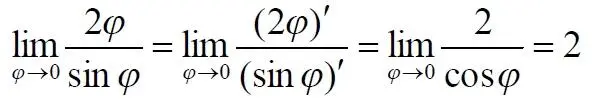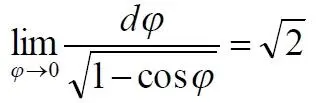Петр Путенихин - Силы тяготения внутри обруча, сферы и между двух точек

Считается, что тело внутри полой сферы не испытывает сил притяжения с её стороны. Рассмотрим такую же ситуацию в плоской форме – силу притяжения тела внутри полого цилиндра. Более того, будем считать, что высота цилиндра равна нулю. Фактически это круг с круглым отверстием внутри.

Очевидно, что ширина этой круговой полосы также качественно не влияет на результаты вычислений, поэтому будем считать её также равной нулю, то есть, рассмотрим очень тонкий массивный обруч.

Для точного определения сил, действующих на тело внутри обруча, рассмотрим дифференциал массы обруча, массу каждого элементарного, бесконечно малого его участка, которая равна

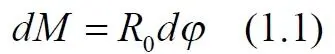
Определим расстояние r между массой m и дифференциальным элементом

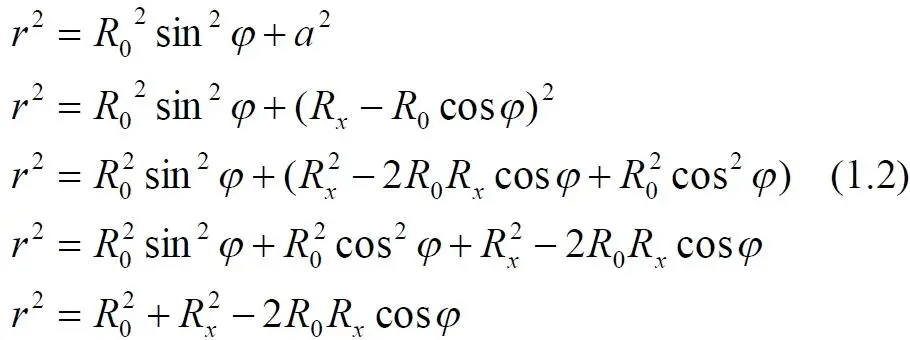
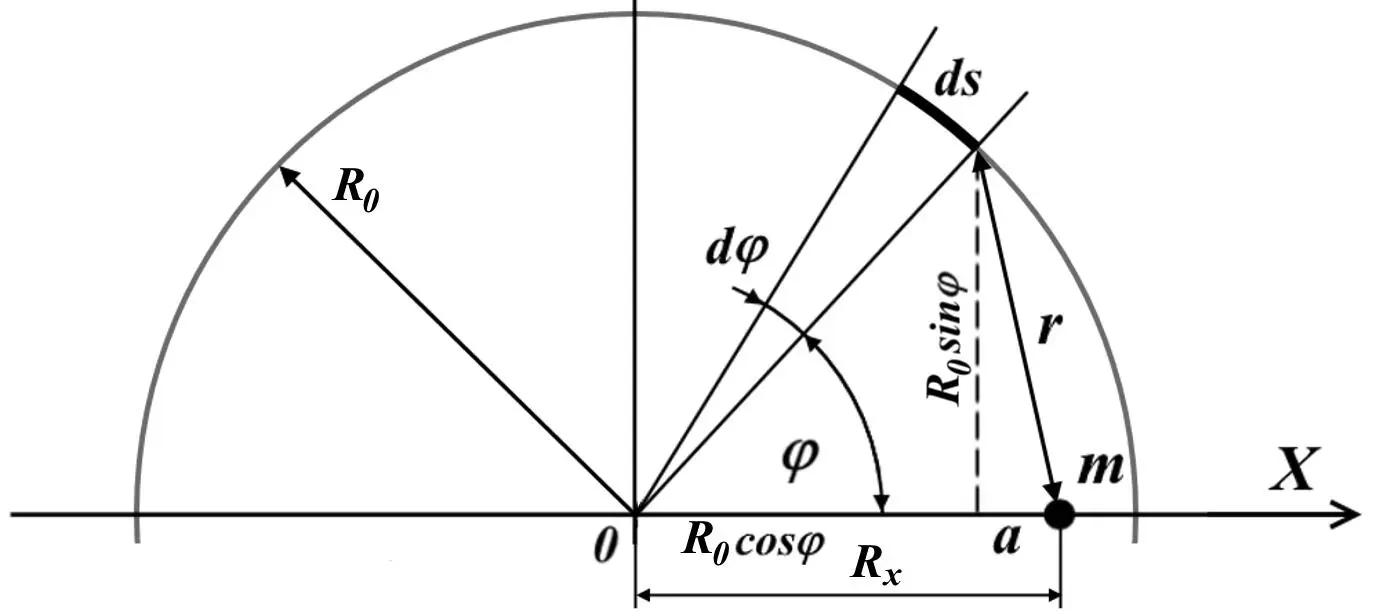
Рис.1.1.Определение силы притяжения тела внутри обруча.

С учетом m = 1, ρ = 1 и вычисленного квадрата радиуса сила притяжения равна

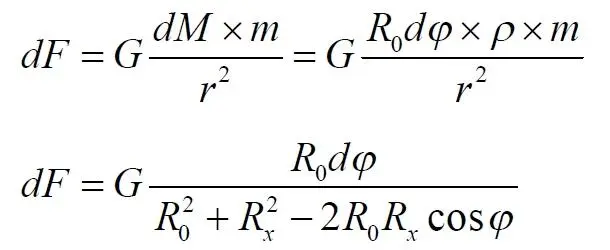
Нас интересует сила, направленная вдоль оси X. Определяем её из соотношения подобных треугольников

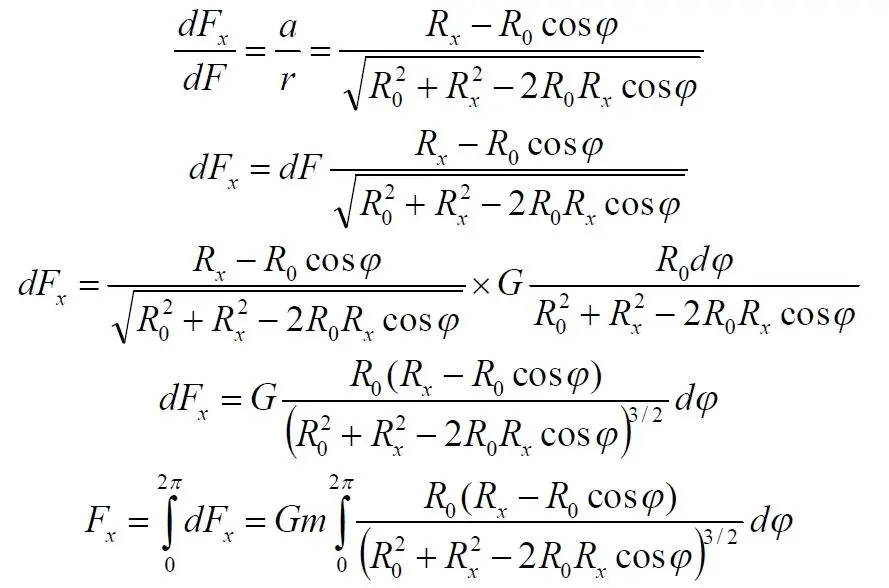
Заменим Rx на долю от R 0, то есть, Rx = kR 0, где, очевидно, k = 0…1

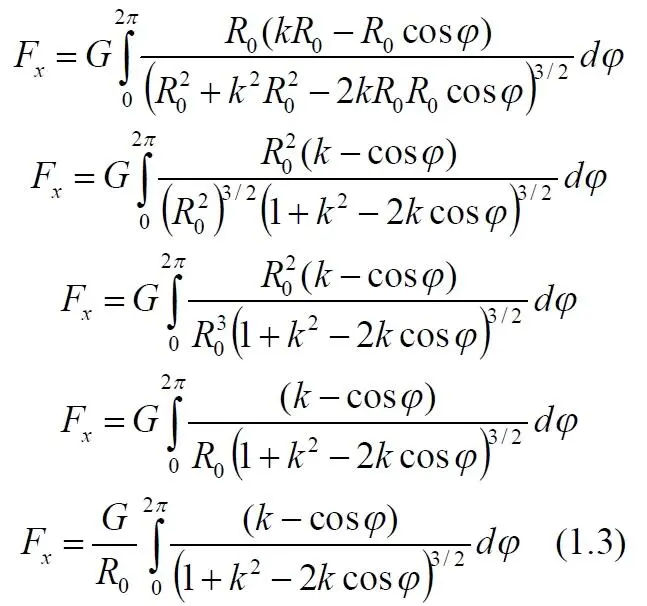
Вычисляем значение силы для каждого значения R xили значения k. Очевидно, что ни одно из значений силы, кроме k = 0, не равно нулю. При этом значении интеграл упрощается до элементарного

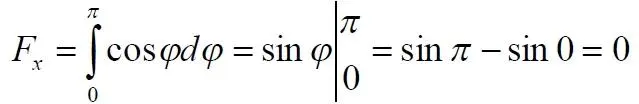
Вероятно, значение силы тем больше, чем ближе R xк R 0. При этом следует ожидать даже бесконечно больших значений при значении k = 1

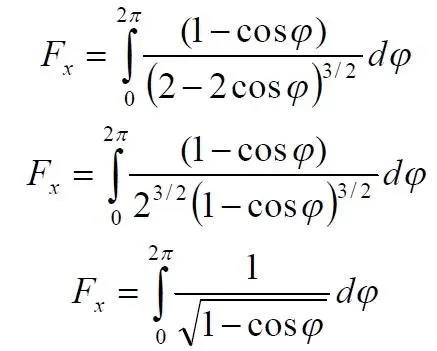
В точке φ = 0 подынтегральная функция обращается в неопределённость, деление нуля – dφ на ноль. Попробуем разрешить эту неопределённость. Поскольку мы производим численное интегрирование, то эта точка соответствует конечным, компьютерным значениям дифференциала и функции φ = dφ =0, то есть, неопределённость 0/0

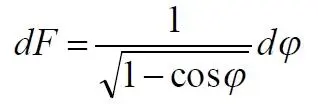
Попробуем разрешить неопределённость аналитически. Вблизи этой точки дифференциал dφ и аргумент φ одинаково стремятся к нулю, поэтом обозначим их одной переменной. Найдём предел отношения подынтегральной функции

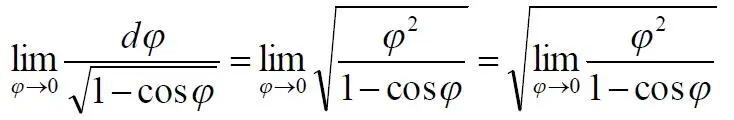
Известно, что предел отношения функций равен пределу отношения их производных

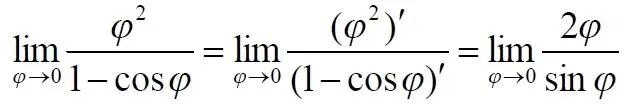
Повторим процедуру замены функций на их производные

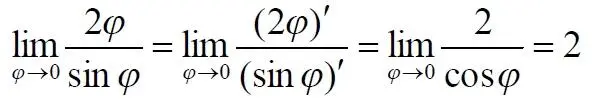
Ранее мы извлекли функцию из-под корня, теперь возвращаем

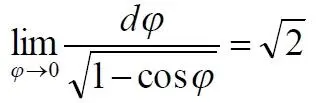
Казалось бы, при нулевом расстоянии между фрагментом обруча и материальной точкой m сила притяжения должна быть равна бесконечность. Однако мы рассматриваем одновременно с уменьшением дистанции и уменьшение длины этого фрагмента, что и привело к конечному значению неопределённости. Другим объяснением может служить то, что расстояние между объектом m и элементом обруча при стремлении его к нулю фактически заменяется в пределе их слиянием . Теперь это не расстояние между ними, это их общий размер. Иначе говоря, два элемента слились своими центрами, а на тело, находящееся в центре массивного объекта, не действуют никакие силы.