Петр Путенихин - Правила счета элементов бесконечного множества

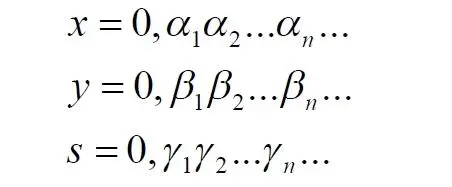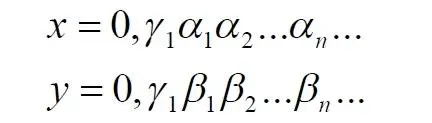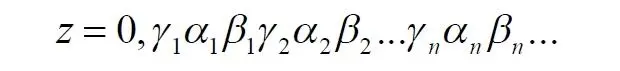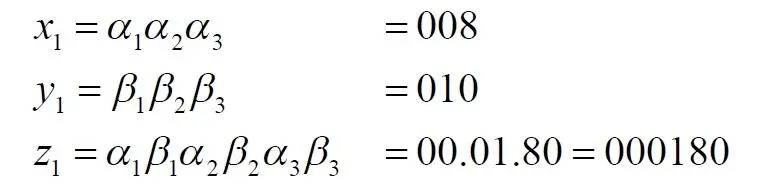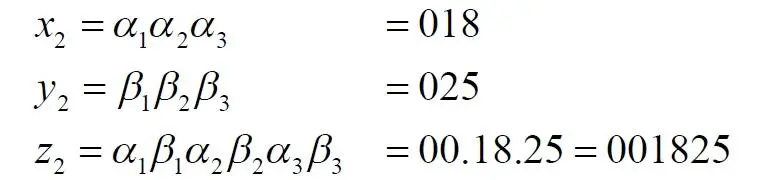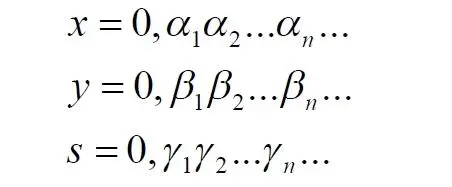
Для простоты, что, вообще-то, усложняет наше опровержение, ослабляет его, возьмём значения этих координат в кратчайшем виде, в виде единственной цифры от 0 до 9 без последующих дополнительных нулей, что во много раз увеличит число таких комбинированных точек, принадлежащих каждому квадрату. Для определенности возьмем в кубе 10 сечений, причем имеющие точное значение координаты s = 0; 0,1; 0,2 … 0,9. Теперь создадим по методу Кантора новые числа для точек каждого квадрата. Согласно этому методу каждая точка квадрата будет описываться новым числом – индексом. Исходные координаты задаём в следующем формате:

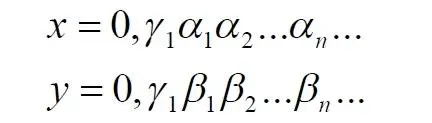
из которых формируем индекс:

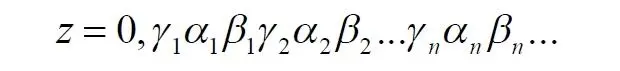
Здесь символом γ обозначен номер квадрата или, что то же самое, его координата в исходном кубе. Например, точки квадрата с номером s = 0,5 будут описываться индексом:

Как видим, закономерно и оправданно все точки и, соответственно, скомбинированные числа отличаются друг от друга, а все точки этого квадрата расположатся на интервале 0,5…0,6 отождествляемой линии и, более того, на линии останется бесконечное число точек, которым не будет соответствовать ни одна точка этого квадрата. Это точки, для которых индекс должен был бы содержать вместо нулей в позициях, кратных трём, другие цифры. Ничего не изменится, если цифру координаты s ставить в тройках последней.

Такая же ситуация будет наблюдаться с индексами и других девяти квадратов. Легко обнаружить, что комбинированные числа каждого квадрата изменяются в диапазонах, соответственно, [0, 0.1), [0.1, 0.2), [0.2, 0.3) и так далее. Таким образом, мы разместили все точки десяти квадратов на одной линии [0, 1]. Получается, что мощность множества, количество точек квадрата имеет меньший порядок, чем мощность множества точек любой линии. В нашем случае – в десять раз. Но мы могли использовать и другое количество квадратов. Тогда и их точки оказались бы во взаимном однозначном соответствии с точками части отрезка. В этом случае соотношение мощностей станет еще больше и даже, по желанию, в любое число раз.

Очевидно, что такой принцип "сколько будет? а сколько надо?", к которому, по сути, сводится метод Кантора, не может служить основой для корректного математического приема. Но в чем же состоит хитрость, изюминка, так сказать, канторовского метода отождествления? По какой загадочной причине происходит такое противоестественное отождествление? В чем его тайный механизм? Ведь мы же четко видим, что каждой точке квадрата можно однозначно привязать каждую точку линии, причем ни одна из точек не останется без своей единственной пары. А тайна, в сущности, предельно проста. Покажем это на еще одном несколько отвлеченном, но подобном примере.

Возьмем для лучшей визуализации квадрат с бесконечным числом точек в количестве… 1000х1000. Конечно, это на самом деле не бесконечность, но число все-таки очень большое – миллион точек, пересчитать которые вручную будет весьма непросто.

Выберем на этом квадрате одну линию, нижнюю грань квадрата. Согласно методу Кантора присвоим какой-то точке квадрата индекс:

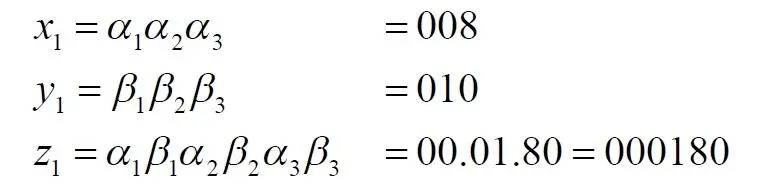
Здесь индекс z сначала представлен с разделительными точками, чтобы было видно, как он образован. Итак, мы получили число z , которое, видимо, точно имеется на отрезке [0, 999]. Правда, настораживает число нулей в этом индексе. Поэтому возьмем для уточнения другую точку на квадрате:

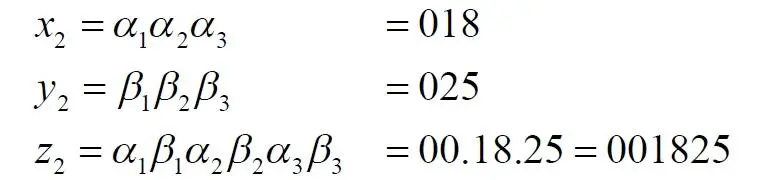
Что-то у нас, как видим, пошло не так. Сразу же можно сделать вывод: на линии [0, 999] такой точки точно нет. В чем же дело? Мы в точности следовали методу Кантора, просто используя отрезок не [0, 1], а более длинный [0, 999]. Принцип тот же, а размеры фигур явно не должны влиять на результат. Иначе получается противоречие: квадрат и линия размером [0, 1] тождественны по мощности, а квадрат и линия [0, 999] имеют уже разные мощности.