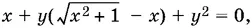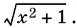9.20.Первые два уравнения системы симметричны относительно x и у . Нужно использовать эту симметрию для того, чтобы получить одинаковые правые части у этих двух уравнений.
9.21.Если второе уравнение возвести в квадрат, то можно сравнить два выражения для ( x + у )². (!)
9.22.В первое уравнение входит у , в последующие уt , yt ² и yt ³ соответственно. Эта закономерность позволяет исключить у .
9.23.Каждый элемент, стоящий в левой части второго уравнения, получается из соответствующего элемента, стоящего в левой части первого уравнения, возведением в квадрат. Нужно использовать это свойство системы.
9.24.Левые части всех трех уравнений симметричны относительно x , у , z . Поэтому, подвергнув какому-то преобразованию любые два уравнения системы, разумно сделать то же самое и с оставшимися двумя парами уравнений.
9.25.Если известна сумма s = x 1+ x 2+ ... + x n , то из каждого уравнения можно найти соответствующее x k .
9.26.Чтобы избежать возведения двучлена в третью и, тем более, в пятую степень, нужно ввести новые неизвестные так, чтобы выражение 7 x − 11 у было одним из этих неизвестных.
9.27.Поскольку 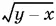 входит в оба уравнения с разными знаками, а √ у — с одинаковыми, то естественно сложить данные уравнения и вычесть. При этом мы приходим к системе, у которой слева стоят сумма и разность одинаковых радикалов, а справа — разные радикалы.
входит в оба уравнения с разными знаками, а √ у — с одинаковыми, то естественно сложить данные уравнения и вычесть. При этом мы приходим к системе, у которой слева стоят сумма и разность одинаковых радикалов, а справа — разные радикалы.
9.28.Чтобы левые части уравнений стали однородными относительно неизвестных, удобно ввести новое неизвестное z = √ у .
9.29.Если каждое из уравнений возвести в квадрат, то получим систему относительно u = x ² и v = у ². Проверка здесь может оказаться довольно сложной, поэтому целесообразно следить за равносильностью в процессе решения. Чтобы в результате возведения в квадрат не появились посторонние решения, достаточно записать ограничения: x > 0, у > 0.
9.30.Все члены системы, содержащие x и у , однородны второй степени относительно x и у . Пусть данная система имеет решения x 1, у 1, z 1Укажите симметричное решение, которое наряду с этим будет иметь система.
9.31.Поскольку вместе с условием x + у = 0 мы получаем три уравнения с двумя неизвестными, то имеет смысл воспользоваться подстановкой у = − x .
9.32.Поскольку данная система должна иметь решение при любом b , то, чтобы сузить область допустимых значений а , можно рассмотреть эту систему при некотором фиксированном b .
9.33.Вначале нужно использовать условие, что система должна иметь только одно решение. Второе уравнение можно рассматривать как четную функцию относительно x и у , т. е. наряду с решением x = x 1, у = у 1оно имеет три симметричных решения: (− x 1, у 1), ( x 1, − у 1), (− x 1, −у 1). Какое из этих решений наряду с ( x 1, у 1) будет удовлетворять первому уравнению?
9.34.Второе уравнение можно преобразовать к виду
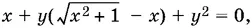
умножив числитель и знаменатель дроби на выражение, сопряженное знаменателю. Легко убедиться, что у ≠ 0. Поэтому можно полученное уравнение разделить на у , после чего нетрудно с помощью первого уравнения системы исключить 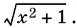
9.35.Представить уравнение в виде
|6 − | x − 3| − | x + 1|| = а ( x + 5) + 4,
построить график функции, стоящей в левой части равенства, и рассмотреть поведение относительно этого графика прямой у = а ( x + 5) + 4 при разных значениях а .
9.36.Обе части нужно возвести в квадрат. Чтобы обеспечить равносильность, в системе с полученным уравнением придется решать неравенство 4 x ² − 3 аx ≥ 0. При этом выражение под вторым радикалом автоматически будет неотрицательным.
В задачах с параметрами, как правило, нарушать равносильность нецелесообразно. Рассуждения, связанные с ОДЗ, не дают строгого решения.
9.37. x = 0 — корень уравнения. Выражения в знаменателях имеют одинаковую составляющую 5 x ² + 6.
9.38.Это система однородных уравнений, и она решается стандартной подстановкой x + у = u , xу = v .
Читать дальше
Конец ознакомительного отрывка
Купить книгу

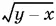 входит в оба уравнения с разными знаками, а √ у — с одинаковыми, то естественно сложить данные уравнения и вычесть. При этом мы приходим к системе, у которой слева стоят сумма и разность одинаковых радикалов, а справа — разные радикалы.
входит в оба уравнения с разными знаками, а √ у — с одинаковыми, то естественно сложить данные уравнения и вычесть. При этом мы приходим к системе, у которой слева стоят сумма и разность одинаковых радикалов, а справа — разные радикалы.