8.15.Если многочлен четвертой степени с коэффициентом 6 при старшем члене делится на x ² − x + q без остатка, то в частном обязательно получится многочлен 6 x ² + аx + b , в котором а и b определяются одновременно с p и q .
9.1.Точки −2, −1, 0 делят числовую ось на четыре интервала, в каждом из которых нужно решить данное уравнение. (!)
9.2.Если рассматривать значения x , обращающие в нуль числа, стоящие под знаками абсолютных величин, то придется разбить числовую ось на пять частей.
Удобнее ввести новое неизвестное у = x ². (!)
9.3.Это уравнение четвертой степени. Следовательно, нужно найти искусственный прием, приводящий к его решению. Удобно воспользоваться тем, что слева стоит сумма квадратов.
9.4.Возвести в куб и сравнить полученное уравнение с данным.
9.5.Свести уравнение к симметрической системе, обозначив первое слагаемое левой части через u , а второе через v . (!)
9.6.Если под радикалами раскрыть скобки, то получим квадратные трехчлены, отличающиеся лишь свободным членом. Поэтому данное в условии уравнение удобно заменить системой, обозначив первое слагаемое его левой части через u , а второе через v .
9.7.Поскольку неизвестное входит в уравнение либо в сочетании x − b , либо в сочетании а − x , то удобно ввести обозначения 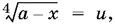
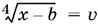 и получить систему алгебраических уравнений.
и получить систему алгебраических уравнений.
9.8.Ввести вспомогательное неизвестное у и свести решение данного уравнения к решению системы уравнений относительно x и у .
9.9.Перенести 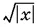 в правую часть уравнения и возвести обе части в квадрат.
в правую часть уравнения и возвести обе части в квадрат.
9.10.Чтобы избавиться от знаков абсолютной величины, можно поступить двояко: либо потребовать, чтобы правая часть уравнения была неотрицательной, и решить уравнения
x ² − 3 x / 2− 1 = − x ² − 4 x + β, x ² − 3 x / 2− 1 = x ² + 4 x − β;
либо рассмотреть два случая: в первом выражение, стоящее под знаком абсолютной величины, неотрицательно, а во втором — отрицательно.
9.11.Рассмотреть различные случаи расположения x и у по отношению к нулю (всего придется рассмотреть четыре случая). (!)
9.12.Решить систему уравнений с параметром k , а затем решить систему неравенств. (!)
9.13.Рассмотреть различные случаи взаимного расположения чисел x и у и чисел x и − у . Это позволит раскрыть знаки абсолютной величины. (!)
9.14.Второе уравнение — уравнение окружности радиуса √ а . Нарисовать кривую, которая определяется первым уравнением.
9.15.Одно решение очевидно: x = у = 0. Если ху ≠ 0, то можно разделить первое уравнение на ху, а второе на x ² у ².
9.16.Если бы во втором и третьем уравнениях не было коэффициентов 2 и 3, то уравнения системы получались бы друг из друга с помощью циклической перестановки неизвестных x , у и z . Однако влияние коэффициентов оказывается столь сильным, что попытка использовать это свойство системы не приводит к успеху. Попытайтесь преобразовать систему в распадающуюся, для чего потребуется отыскать алгебраическое выражение, общее для двух уравнений, и исключить его.
9.17.Если первое уравнение системы записать в виде x + у = − z и возвести в квадрат, то с помощью второго ее уравнения можно найти ху .
9.18.Сопоставьте первое и последнее уравнения. Если записать их в виде
x + у = 1 − z , х ³ + у ³ = 1 − z ³,
то напрашивается способ, с помощью которого можно преобразовать систему в распадающуюся.
9.19.Если раскрыть скобки, то получим систему линейных уравнений относительно u = x + у + z , v = ху + xz + yz , w = xyz. Найдя u , v и w , можно вычислить х ³ + у ³ + z ³, если возвести x + у + z = u в куб: u ³ = х ³ + у ³ + z ³ + 3 uv − 3 w .
Однако такой путь решения, хотя и прост по идее, требует значительных выкладок. Решение можно упростить, если ввести в рассмотрение многочлен M ( t ) = ( t − x )( t − у )( t − z ) + а, который в силу условия задачи имеет корни t = а, t = b , t = с .
Читать дальше
Конец ознакомительного отрывка
Купить книгу

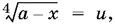
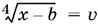 и получить систему алгебраических уравнений.
и получить систему алгебраических уравнений.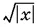 в правую часть уравнения и возвести обе части в квадрат.
в правую часть уравнения и возвести обе части в квадрат.










