Задача существенно упростится, если удастся выбрать в кубе простейшую фигуру, составленную из плоских фигур, которая отбрасывает на плоскость Π ту же самую тень.
5.1.Если точка M принадлежит геометрическому месту точек, то отрезок NО виден из нее под прямым углом. (!)
5.2.Если к треугольнику АМВ применить теорему косинусов, то получим еще одно соотношение, связывающее угол АМВ со сторонами треугольника.
5.3.Поскольку характеристики геометрического места точек содержатся в условии задачи, вполне удобно доказать, что любая точка окружности обладает указанным свойством. Для этого следует применить теорему косинусов к стороне МВ треугольника АМВ .
5.4.При любом выборе точки M треугольники АМВ и ВМС имеют общую сторону ВМ . Использовать условие равновеликости двух треугольников, имеющих общую сторону.
5.5.Пусть точка M зафиксирована. Площадь треугольника АВМ не изменится, если отрезок AB двигать по прямой AB . То же самое можно сказать о треугольнике СDМ . Остается рассмотреть два случая: 1) прямые AB и CD пересекаются, 2) прямые AB и CD параллельны.
5.6.Выясните, какую роль играет в задаче куб. Задачу можно разделить на две: вначале решить ту же задачу для прямых , на которых расположены диагонали куба, а затем высечь часть пространства, ограниченную кубом, и проследить, какие при этом произойдут изменения.
6.1.Воспользоваться тождеством p ² − 1 = ( p − 1)( p + 1).
6.2. Способ 1.Воспользоваться методом математической индукции. (!)
Способ 2.Разбить все числа на классы по модулю 3:
n = 3 k , n = 3 k + 1, n = 3 k − 1,
и проверить утверждение для каждого класса. (!)
6.3.Поскольку 105 = 3 · 5 · 7, то а 105= ( а ³) 35= ( а 5) 21= ( а 7) 15. Воспользуйтесь этим для разложения данного числа на множители.
6.4.Среди чисел от 1 до 500 будет 250 четных, 125 делящихся на 4 и т. д.
6.5.Чтобы данное число приняло более симметричный вид, его удобно умножить на 10. При этом делимость его на 81 не изменится.
6.6.Дополнить выражение n 4+ 4 до полного квадрата и разложить на множители.
6.7.Так как по условию n четное, то нужно сделать подстановку n = 2 k и привести данное выражение к общему знаменателю.
6.8. Способ 1.Дробь 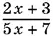 сократима тогда и только тогда, если ее числитель представим в виде pr , а знаменатель — в виде qr , где p , q и r — целые числа и r ≠ ±1.
сократима тогда и только тогда, если ее числитель представим в виде pr , а знаменатель — в виде qr , где p , q и r — целые числа и r ≠ ±1.
Способ 2.Если сократима дробь p / q , то сократима и дробь q / p .
6.9.Использовать сначала признак делимости на 4, а затем признак делимости на 9. (!)
6.10.Если условие, в силу которого число 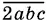 в три раза меньше
в три раза меньше 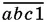 записать символически, то получим уравнение, которое нужно будет решить в целых числах, каждое из которых расположено между 0 и 9.
записать символически, то получим уравнение, которое нужно будет решить в целых числах, каждое из которых расположено между 0 и 9.
6.11.Ясно, что число p нечетное. Одно значение p легко угадать — это p = 3. Есть ли другие?
6.12.Задачу удобнее решать от противного, исходя из предположения, что tg 5° = p / q , где p и q — целые.
6.13.Если меньшее из чисел не оканчивается цифрой 9, то суммы цифр этих чисел различаются на 1. Поэтому обе суммы цифр одновременно делиться на 11 не могут. Нужно искать решение среди чисел, меньшее из которых оканчивается одной или несколькими цифрами 9.
6.14.Нужно правильно использовать условие, в силу которого x и у — целые. Однородное выражение относительно неизвестных нужно оставить слева и попытаться разложить на множители, а число 17 перенести в правую часть равенства.
6.15.Данное уравнение таково, что если x = а , у = b — его решение, то существуют еще три решения: (− а , b ), ( а , − b ), (− а , − b ), если а ≠ b .
6.16.Преобразовать исходное условие к виду 11(4 x − 1) = 69( у − x ) и воспользоваться тем, что x и у — натуральные числа.
7.1.Обе двойки представить как 3 − 1 и сгруппировать члены так, чтобы в числителе можно было вынести за скобки n + 1, а в знаменателе n − 1.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

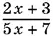 сократима тогда и только тогда, если ее числитель представим в виде pr , а знаменатель — в виде qr , где p , q и r — целые числа и r ≠ ±1.
сократима тогда и только тогда, если ее числитель представим в виде pr , а знаменатель — в виде qr , где p , q и r — целые числа и r ≠ ±1.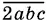 в три раза меньше
в три раза меньше 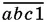 записать символически, то получим уравнение, которое нужно будет решить в целых числах, каждое из которых расположено между 0 и 9.
записать символически, то получим уравнение, которое нужно будет решить в целых числах, каждое из которых расположено между 0 и 9.










