Александр Берлин - Математика рынка. Сборник задач

© Александр Берлин, 2019

ISBN 978-5-4490-2585-2

Создано в интеллектуальной издательской системе Ridero

Эта книга дополняет теоретические положения уже опубликованных книг в [3.1,3.2,3.3].

В ней рассматриваются вопросы, которые возникают на различных этапах функционирования рынка и предлагаются их решения с помощью методов теории массового обслуживания. Применение предлагаемых математических методов позволяет проводить строгие расчеты искомых показателей.

– На начальном этапевнедрения товара на рынок возникают вопросы.

1.Величины спроса на этот товара

2.Возможные доходы.

3.Надёжность возврата кредита (в случае его получения).

– На этапе поставокрассматриваются вопросы конкуренции.

– Как влияет поведение на рынке конкурентов (повышение поставок товаров или их снижение).

– Как влияет на спрос появление на рынке новых конкурентов.

– Как влияют внешние факторы (катастрофы, погода и другие).

– Ценовая политика. Процентные ставки, денежная масса.

– При этом рассматриваются свойства самого рынка.

1 Количество поставщиков.

2.Однородность поставляемых товаров.

3. Зависимость спроса от момента времени.

4. Дисциплина обслуживания товара – без накопления непроданных товаров и накоплением на складах.

5. Стратегия поведения поставщиков в случае перепроизводства.

Практика показала, что подробное последовательное изучение определений и классификация понятий затрудняет понимание сути дела. Потому будем излагать материал, опираясь на интуицию и опыт читателя.

Математические доказательства можно посмотреть в книгах

(1.1, 2.1,3.1,,3.2, 3.3)).

Решение этих вопросов рассмотрим в следующем порядке.

– Вначале рассмотрим предлагаемую математическую модель, которая нам поможет сделать математическую постановку задачи.

– Определим, что такое товар и введём основную единицу измерения, которая позволит нам анализировать любые товары (Что общего между товаром «крокодил» и товаром «идея»? ).

– Рассмотрим формулы, позволяющие определить характеристики спроса и предложения для заданной сети.

– Рассмотрим примеры решения задач для конкретных рынков (например, расчет рынка нефти, вопросы предотвращения перегрузки рынка, определение необходимого числа покупателей для заданного процента потерь).

Для математической оценки процессов, происходящих в экономике необходимо создать модель, которая позволила бы отразить их в математическом виде. Совместно с определением единицы измерения спроса и предложения – относительного потребления, эта модель позволяет получить и обеспечить количественный расчет, анализ и оценку возможного поведения рынка. Предлагаемая модель показана на рис.1.1.

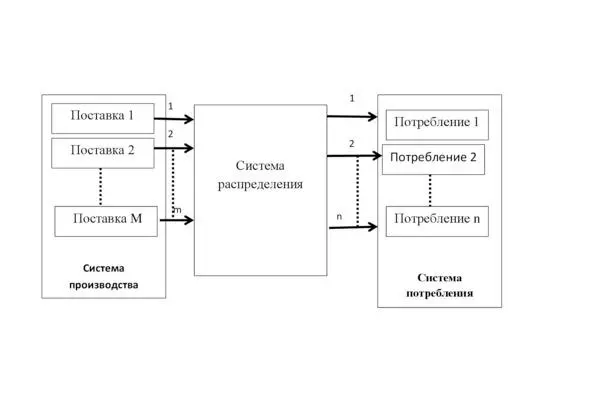
Рисунок 1.1.Математическая модель рынка

Система производства – порождает случайный поток товаров (в общем случае отличающихся друг от друга). Под товаром понимается, любое изделие или услуга, предлагаемая для продажи, в которой имеется потребность, (в дальнейшем будет показано, как определить потребность в числовом виде). Это могут быть предметы питания, например, молоко и другие продукты питания, автомобили, дома, услуги по уборке дома, акции, строительные фирмы, предлагающие услуги по строительству домов и т. д.

Поток поступает в систему распределения.

Система распределения, может обслужить заказ немедленно или с какой-то задержкой. Задержка может быть двух типов:

– отказ в приёме товара из-за отсутствия спроса;

– или установка на ожидание реализации (накопление не проданных товаров)

Возможны два типа систем распределения.

Первые из них ставят задачу максимально быстро реализовать товар без всяких дополнительных условий. В теории массового обслуживания такая система распределения заявок на обслуживание называется полнодоступной, поскольку обеспечивает равный доступ к системе потребления и при расчётах поведения рынка – может не учитываться.

Системы второго типа распределяют товары, учитывая заданные приоритеты и ограничения для отдельных потребителей или систем потребления. Например, продажа табака, алкоголя, оружия… Системы этого типа называются неполнодоступными.