Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

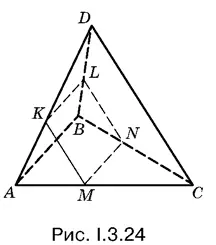
3.24.Чтобы в сечении получился квадрат, плоскость сечения необходимо провести так, чтобы она пересекала все четыре грани пирамиды (иначе мы получили бы в сечении треугольник). Докажите, что если KLNM — квадрат (рис. I.3.24), то плоскость KLNM параллельна двум скрещивающимся прямым AB и СD .

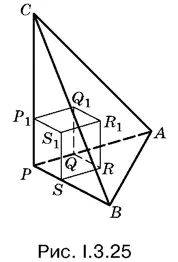
3.25.Для того чтобы найти наиболее рациональное решение задачи, поставьте пирамиду на одну из боковых граней (рис. I.3.25), а затем примените сравнение объемов.

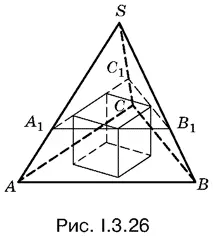
3.26.Вписать в пирамиду куб значит расположить его так, чтобы нижнее основание куба лежало на основании пирамиды, а верхнее основание куба было вписано в треугольник, полученный в горизонтальном сечении пирамиды (рис. I.3.26).

3.27.K решению этой задачи удобно подойти аналитически, рассмотрев общий случай. Предположим, что в сечении образовался некоторый треугольник со сторонами а , b и с . Полезно рассмотреть пирамиду, в основании которой лежит этот треугольник, а вершиной является вершина трехгранного угла.

3.28.По условию задачи попарно равны именно те ребра тетраэдра, которые лежат на скрещивающихся прямых. Использовать это условие можно, если расположить тетраэдр так, чтобы ребро AB лежало в горизонтальной плоскости P , а ребро DС было параллельно этой плоскости.

3.29.Нужно построить расстояние между прямыми AB и CD . Для этого через один из отрезков, например через AB , надо провести плоскость P , параллельную CD .

Решение естественно начать с построения плоскости P , проходящей через одно ребро ( AB ) и параллельной другому ( CD ). Удобный чертеж можно получить, повернув пирамиду вокруг AB так, чтобы плоскость P стала горизонтальной.

Далее нужно построить угол между скрещивающимися прямыми AB и CD . Напомним, что для этого достаточно построить прямую, пересекающую одну из них и параллельную другой.

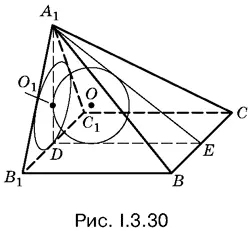
3.30.Плоскость А 1 ВС отсекает от призмы четырехугольную пирамиду. Расположим ее так, как показано на рис. I.3.30. То, что в эту пирамиду вписан шар радиусом R , означает, что в треугольники В 1 А 1 С 1и DА 1 Е вписаны окружности радиусом R .

3.31.В силу соображений симметрии центр шара, о котором идет речь в задаче, совпадает с центром шара, вписанного в правильный тетраэдр.

3.32.Если куб преобразовать подобно, выбрав в качестве центра подобия точку О , то диагональ, проходящая через точку О , сохранит свое направление в пространстве.

3.33.Составным элементом этой задачи является соотношение, связывающее разность углов треугольника, прилегающих к некоторой его стороне, с углом между этой стороной и биссектрисой противоположного угла.

3.34.Диагонали, расстояние между которыми нужно найти, будут лежать на скрещивающихся прямых. Расстояние между скрещивающимися прямыми равно расстоянию между определяемыми ими параллельными плоскостями.

3.35.Так как сфера с центром в точке О расположена симметрично относительно всех трех ребер, выходящих из А , то О должна лежать на диагонали куба.

3.36.Вначале нужно извлечь информацию из того обстоятельства, что проекции каждой стороны четырехугольника на взаимно перпендикулярные плоскости равны. Отсюда следует, что каждая сторона четырехугольника параллельна плоскости, делящей угол между взаимно перпендикулярными плоскостями пополам.

3.37.Задачу можно свести к такой: доказать, что объем конуса меньше куба его образующей. (!)

3.38.Введите линейные элементы, характеризующие конус, например высоту H и радиус основания ρ. Затем величины H , ρ и p выразите через радиусы R и r шаров.

3.39.Чтобы использовать данное в условии отношение объемов двух конусов, нужно выразить радиус основания одного конуса через радиус основания другого. Для этого придется внутренний конус, свободно вращающийся в шаре, закрепить так, чтобы образующие конусов были параллельны.