Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

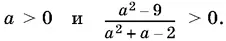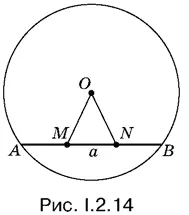
2.15.Так как длина отрезка PQ и несущая его прямая известны, то можно воспользоваться методом параллельного переноса.

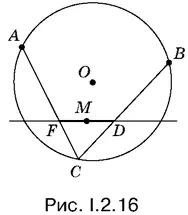
2.16.Нужно построить отрезок FD (рис. I.2.16), делящийся в точке M пополам. Следовательно, его можно рассматривать как одну из диагоналей параллелограмма. В качестве одной из вершин параллелограмма удобно выбрать точку В . Отразив ее симметрично от точки M , получим еще одну вершину.

2.17.Если через точки А и В провести прямую, то она, вообще говоря, должна пересечь прямую PQ в некоторой точке С . Остается воспользоваться свойством секущей и касательной, проходящих через общую точку. Случай, когда AB и PQ параллельны, рассмотрите отдельно. (!)

2.18.Соединить точку M с концами А и В данного диаметра. Рассмотреть получившиеся точки пересечения с окружностью.

2.19.Воспользоваться предыдущей задачей и построить произвольный перпендикуляр к данному диаметру, пересекающий окружность в точках С и D .

2.20.Какую бы точку С на прямой l мы ни взяли, величина | AC − BC | в силу неравенства треугольника не может превзойти длины отрезка AB . Следовательно, существует точка прямой l , отвечающая требованиям задачи. По условию точки А и В лежат по разные стороны прямой l . Принципиально ли это требование, или же можно сформулировать эквивалентную задачу для точек, лежащих по одну сторону прямой l ?

2.21.Для построения естественно воспользоваться обычным методом геометрических мест. Каждая вершина квадрата лежит на внешней половине окружности, построенной на стороне четырехугольника как на диаметре. Чтобы отыскать второе геометрическое место точек, которому принадлежат вершины, нужно выяснить, что связана какая-то из линий, определяющих вершины, с данным четырехугольником. Рассмотрите с этой целью диагональ квадрата.

2.22.Дан отрезок и известно, что его длина 7. Отрезок длины 1 не известен. Если бы он был дан, то отрезок длины √7 можно построить, как только мы построим отрезок длины √3. Затем построим гипотенузу прямоугольного треугольника со сторонами √3 и 2.

2.23.Решение можно искать только при одновременном выполнении условий:

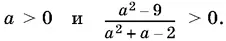
3.1.Чтобы связать участвующие в задаче элементы, нужно отрезок ОА луча, перпендикулярного к ребру, спроецировать на другую полуплоскость. Проекцию ОВ этого отрезка спроецировать в отрезок ОС , лежащий на втором луче.

3.2.Чтобы связать данные углы с величиной угла, который нужно найти, следует спроецировать катеты треугольника на плоскость P и построить искомый угол.

3.3.При проецировании угла α на плоскость P возникает четырехгранный угол, в котором три плоских угла даны, а два двугранных угла прямые. Чтобы установить связь между плоскими углами, нужно пересечь этот четырехгранный угол плоскостью Q , перпендикулярной к плоскости P .

3.4.Если спроецировать искомую прямую, параллельную а , на плоскость, перпендикулярную к а , то мы получим точку. Спроецируйте на эту же плоскость три оставшиеся прямые.

3.5.Начать нужно с построения искомого угла. Для этого прямые AB и SC нужно перенести в одну точку. Если сместить прямую SC , то она «повиснет в воздухе» и угол, который мы получим, не будет связан с треугольником. Поэтому проведем через току C прямую CD , параллельную AB ; угол SCD искомый.

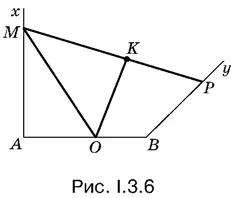
3.6.Лучи Аx и Вy удобно расположить так, как показано на рис. I.3.6. Утверждение, что ОК = АО , равносильно утверждению, что АM = MK (рассмотрите прямоугольные треугольники ОАМ и OKM ).

3.7.Если такое сечение четырехгранного угла существует, то в результате параллельного сдвига плоскости этого сечения мы получим новую плоскость, пересечение которой с четырехгранным углом — тоже параллелограмм. Поэтому строить сечение можно в любой точке ребра четырехгранного угла.