Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

1.40.Из данного отношения площадей треугольников АВС и АDЕ , записанного в виде отношения произведений катетов, и из свойства произведения секущей на ее внешнюю часть найти отношение AE / AB .

1.41.Пусть О 1— центр окружности, радиус которой мы ищем, а О — центр данной окружности. В качестве связующего звена следует рассмотреть треугольник АОО 1.

1.42.Нужно обозначить сторону квадрата через а и составить с помощью теоремы Пифагора биквадратное уравнение для определения а через R и r .

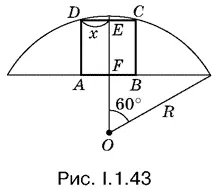
1.43.Вписанный в сегмент квадрат не должен нарушать симметрии сегмента. Поэтому он расположится так, как показано на рис. I.1.43. Обозначим половину стороны квадрата через x и составим уравнение относительно x .

1.44.Чтобы использовать условия задачи, нужно провести радиусы обеих окружностей в точки касания окружностей друг с другом и с нижним основанием. Центр меньшей окружности лежит на биссектрисе угла D .

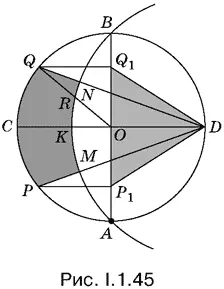
1.45.Вначале для определенности удобно предположить, что точки P и Q лежат по разные стороны от CD . В этом случае диаметр CD разделит фигуры РQNМ и Р 1 Q 1 D на две части (рис. I.1.45). Нужно доказать, что площадь фигуры СQNK равна площади треугольника Q 1 OD . При этом полезен будет следующий факт. Если соединить точки Q и О , то, во-первых, угол QОС вдвое больше угла QDС , а во-вторых, треугольники ОQ 1 D и ОQD равновелики.

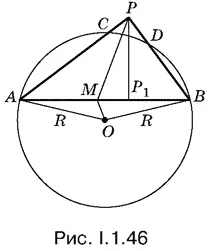
1.46.Соединим точки А и В , P и M и проведем радиусы из центра О в точки А и В (рис. I.1.46). Если длины отрезков AB , АР 1и ОА = R заданы и отрезок AB построен, то прямоугольный треугольник АРВ и положение точки О определяются однозначно. Следовательно, зная длины этих отрезков, можно вычислить длины интересующего нас отрезка РМ .

1.47.Отрезок, соединяющий центр окружности с серединой хорды, перпендикулярен к этой хорде. Зная, что хорда удалена от центра на 3 R / 5, легко выразить ее длину через R .

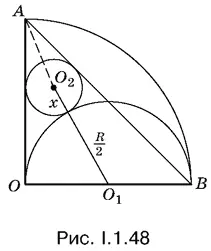
1.48.Использовать геометрически касание окружности О 2с окружностью О 1можно, соединив их центры (рис. I.1.48). Отрезок О 2 О 1пройдет через точку касания. Так как окружность О 2касается сторон угла ОАВ , то ее центр лежит на биссектрисе угла ОАВ .

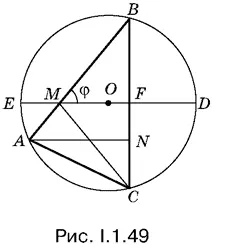
1.49.Если в треугольнике АВС провести высоту АN (рис. I.1.49), то искомая площадь будет равна ½ АN · BC . Соединив точки M и С , разобьем треугольник АВС на равнобедренный треугольник МСВ и треугольник АМС , у которого угол АМС легко выразить через φ.

1.50.Задача вычислительная. Нужно воспользоваться формулой Герона и выражением радиуса R через стороны треугольника и его площадь S , т. е. R = abc / 4 S . Стороны треугольника удобно обозначить: а , а − d , а + d .

1.51.Проведите через точки P и Q прямые, параллельные AC . Первая будет средней линией треугольника АВС , вторая — средней линией треугольника с вершиной В , которому первая средняя линия служит основанием.

1.52.Соединим точки P и T . Данный треугольник разбивается на пять. Пусть QT = m , TL = n , QN = RL = а . Чтобы использовать условия задачи, можно записать соотношения площадей различных треугольников, образовавшихся из данного треугольника PQR .

1.53.Хорда MN — сторона правильного шестиугольника, вписанного в первую окружность, так как опирающийся на MN центральный угол ∠ МО 1 N = 60°. Чем является MN для второй окружности?

1.54.Для вписанного в окружность четырехугольника воспользоваться свойством, в силу которого сумма противоположных его углов равна 180°. Удобно обозначить стороны четырехугольника через а , b , с , d , начиная со стороны AB , а опирающиеся на них углы (проведите диагонали) через α, β, γ, δ.