Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

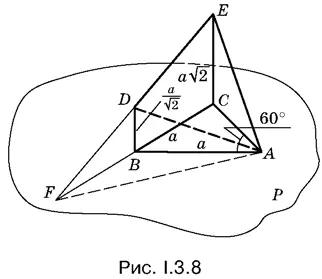
3.8.Если продолжить DE и BC до пересечения в точке F , то BD — средняя линия в треугольнике EFC (рис. I.3.8). Площадь треугольника DEА равна половине площади треугольника FEA .

3.9.Чтобы ответить на вопрос задачи, нужно определить высоту H пирамиды. Каждый из данных двугранных углов можно измерить с помощью линейного угла, опирающегося на высоту H . Остается использовать тот факт, что в основании лежит правильный треугольник.

3.10.Докажите, что высота, проведенная в треугольнике АDВ через вершину D , проходит через середину E основания AB . Тогда интересующий нас двугранный угол измеряется линейным углом DEC .

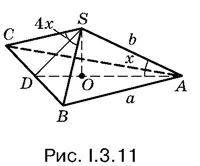
3.11.Условия задачи отражены на рис. I.3.11. Сторона а основания известна, так как известна площадь основания.

3.12.Аналогичное построение на плоскости приводит к образованию треугольника, подобного данному, с коэффициентом подобия ½. Поэтому и здесь следует постараться выяснить, подобны ли рассматриваемые тетраэдры.

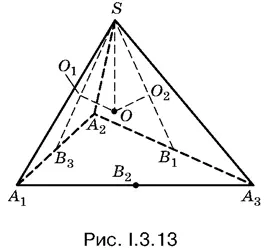
3.13.Если О — центр шара, касающегося боковых граней пирамиды в точках О 1, О 2и О 3(рис. I.3.13), то легко установить, что SB 1= SB 2= SB 3. Если мы сумеем доказать равенство треугольников А 2 SВ 1и А 2 SВ 3, то установим, что в основании пирамиды лежит правильный треугольник.

3.14.Достроить усеченную пирамиду до полной и рассмотреть высоты пирамид, имеющих три основания, о которых идет речь в условии.

3.15.Построить угол между скрещивающимися прямыми можно, если параллельно перенести их так, чтобы они проходили через одну точку. В качестве такой точки удобно выбрать вершину А основания пирамиды. Если мы достроим треугольник АВС , лежащий в основании, до параллелограмма АВСЕ (рисунок сделайте самостоятельно), то угол DАЕ будет искомым. Образовавшаяся в результате четырехугольная пирамида будет состоять из ребер данной длины, за исключением ребра DЕ .

3.16.Тетраэдр разбивается на две пирамиды с общим основанием — плоскостью сечения. Данное отношение объемов позволяет найти отношение высот этих пирамид и, следовательно, отношение синусов искомых углов.

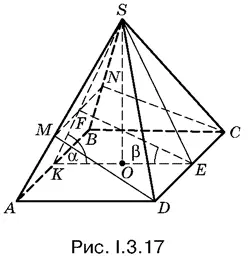
3.17.Условия задачи отражены на рис. I.3.17. Нас интересует отношение площадей треугольников DАМ и DМS , в то время как все известные элементы сосредоточены в плоскости KSЕ . Поэтому нужно связать элементы треугольников DАМ и DМS с элементами треугольника KSЕ .

3.18. Использовать условие задачи, согласно которому высота пирамиды, опущенная из вершины D , проходит через точку пересечения высот основания АВС , с тем, чтобы доказать, что треугольники АDВ и АDС прямоугольные.

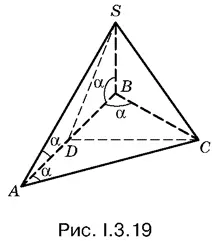
3.19.В пирамиде SАВС (рис. I.3.19) равнобедренные треугольники АSВ и АСВ равны. Следовательно, проведенные в них высоты из вершин S и С упадут в точку D — середину AB .

3.20.Если верхний из двух равных треугольников, лежащих один на другом в плоскости, начать вращать вокруг из общей стороны, то образованный ими двугранный угол может быть как острым, так и тупым. Поэтому придется рассмотреть два случая.

3.21. Если в основании АВС пирамиды провести высоту ВD , то отрезок SD разделит угол АSС пополам.

3.22.Покажите, что отрезки AB и CD взаимно перпендикулярны. Центр описанного шара лежит на их общем перпендикуляре KM , где K — середина СD , M — середина AB .

3.23. Расстояние от основания высоты до бокового ребра измеряется отрезком перпендикуляра, опущенного на боковое ребро. Чтобы связать участвующие в задаче величины, нужно измерить двугранный угол α линейным углом, построенным в точке бокового ребра, которая является основанием этого перпендикуляра. Следовательно, придется построить сечение пирамиды, проходящее через основание высоты и перпендикулярное к боковому ребру пирамиды.