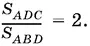Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

1.5.Углы определяют треугольник лишь с точностью до подобия. Если ввести в рассмотрение один линейный элемент и выразить через него обе площади, то при подсчете отношения площадей этот элемент сократится. В качестве такого линейного элемента удобно выбрать радиус r вписанной в треугольник окружности.

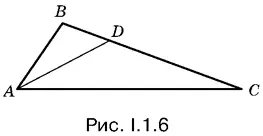
1.6.Так как В = 3 C (рис. I.1.6), то сторона AB меньше стороны AC и можно доказать, что площадь треугольника АВD ( АD — биссектриса треугольника АВС ) меньше площади треугольника ADC . Таким образом по условию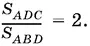

1.7.Применить метод сравнения площадей.

1.8.Все участвующие в задаче величины связаны с площадью треугольника, которая известна. Воспользоваться сравнением площадей.

1.9.В треугольнике даны две биссектрисы и отношение, в котором эти биссектрисы делятся точкой их пересечения. Наряду с данными отношениями естественно воспользоваться свойством отрезков, на которые биссектриса делит противоположную сторону треугольника. Поскольку требуется определить углы треугольника, то от отношений данных линейных величин нужно перейти к отношению сторон данного треугольника.

1.10.Продолжить отрезок QМ до пересечения в точке А с другой стороной угла.

1.11.Известные высоты треугольника естественно связать между собой с помощью его площади. При этом вместо сторон треугольника удобнее рассматривать его углы, выразив стороны через третью высоту.

1.12.В соотношении b + с = k выразить b и с через известную высоту h и тригонометрические функции углов В и С .

1.13. Способ 1.Чтобы решить задачу, нужно установить связь между углом α, сторонами треугольника и его площадью. Однако установить эту связь непосредственно не удается. Поэтому необходимо рассматривать вспомогательные элементы, например перпендикуляры длины x , у и z , опущенные из точки О на стороны а , b , с соответственно.

Способ 2.Чтобы установить связь между углом α, сторонами треугольника и его площадью, можно ввести в рассмотрение длины отрезков: ОА = I , ОВ = m , ОС = n .

1.14.По условию CD = BC − AC ( D — основание высоты). Однако BC и AC можно выразить через CD с помощью тригонометрических функций углов треугольника АВС . Это даст нам уравнение, связывающее углы треугольника АВС .

1.15.Если рассматривать длины сторон AC = b и BC = а, то все участвующие в задаче геометрические величины будут связаны с площадью треугольника ABC.

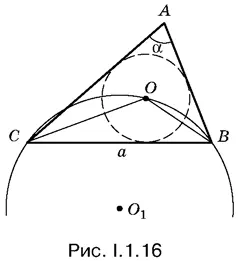
1.16.Чтобы геометрически связать окружность с центром О и окружность с центром О 1, нужно провести отрезки СО и ВО (рис. I.1.16). Окружность О 1описана около треугольника СОВ. Длина хорды СВ известна. Следовательно, для того, чтобы найти радиус, достаточно определить угол СОВ.

1.17.Задачу удобно переформулировать иначе: через центр вписанной окружности проведем прямую, параллельную средней стороне треугольника, и докажем, что она пройдет через точку пересечения медиан, т. е. точка пересечения этой прямой с медианой, опущенной на меньшую сторону, делит медиану в отношении 2 : 1.

1.18.Воспользоваться методом сравнения площадей.

1.19.Точки A , О и L лежат на одной прямой — биссектрисе угла ВАС , аналогично точки В , О и K лежат на биссектрисе угла АВС . Прямая KL делит угол АСМ пополам ( СМ — продолжение BC ).

По условию A = 2 С , а В = 4 С (рисунок сделайте самостоятельно).

1.20.Так как сумма углов в треугольнике равна π, то углы А , В и С нетрудно вычислить.

1.21.Сделать несложное дополнительное построение, чтобы получились подобные треугольники.

1.22.Поскольку отрезки, длины которых входят в правую часть равенства, лежат на одной прямой, нужно выразить длины всех отрезков на той же прямой. Тем самым мы «спрямим» записанное соотношение и сделаем его доказательство простым.