(1 + x ² + х 5) 20= а 0+ а 1 х + а 2 х ² + ... + а 100 х 100.
21.12.Дана последовательность а 1, а 2, а 3, ..., а 10. Сколькими способами, сохраняя фиксированный порядок элементов последовательности, ее можно разбить на группы, каждая из которых состоит из одного элемента или двух рядом стоящих элементов?
21.13.На плоскости проведены m параллельных прямых и n прямых, пересекающих эти прямые и друг друга. Никакие три прямые не проходят через одну точку. На сколько областей (частей) эти прямые разбивают плоскость?
Глава 22
Обратные тригонометрические функции
Определения обратных тригонометрических функций приводят к следующим соотношениям.
Если arcsin x = α (−1 ≤ x ≤ 1), то sin α = x и − π/ 2≤ α ≤ π/ 2.
Если x ≥ 0, то 0 ≤ α ≤ π/ 2; если x ≤ 0, то − π/ 2 ≤ α ≤ 0.
Если arccos x = α (−1 ≤ x ≤ 1), то cos α = x и 0 ≤ α ≤ π.
Если x ≥ 0, то 0 ≤ α ≤ π/ 2; если x ≤ 0, то π/ 2 ≤ α ≤ π.
Если arctg x = α, то tg α = x и − π/ 2< α < π/ 2.
Если x ≥ 0, то 0 ≤ α < π/ 2; если x ≤ 0, то − π/ 2< α ≤ 0.
Если arctg x = α, то ctg α = x и 0 < α < π.
Если x ≥ 0, то 0 < α ≤ π/ 2; если x ≤ 0, то π/ 2 ≤ α < π.
Имеют место следующие соотношения [14] Первое соотношение — неабсолютное тождество, остальные — абсолютные тождества.
:
arcsin x + arccos x = π/ 2; arctg x + arcctg x = π/ 2;
arcsin (− x ) = −arcsin x ; arctg (− x ) = −arctg x ; arccos (− x ) = π − arccos x ; arcctg (− x ) = π − arcctg x .
22.1.Докажите, что
2 arctg ¼ + arctg 7/ 23= π/ 4.
22.2.Представьте выражение
arctg 7/ 9+ arcctg 8 + arcsin √2/ 4
в виде значения функции arcsin x .
22.3.Представьте выражение
arctg (−2) + arcsin ⅓ + arctg (−⅓)
в виде значения лишь одной обратной тригонометрической функции.
22.4.Вычислите сумму
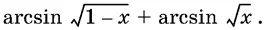
22.5.Найдите
arccos (sin π( x ² + x − З)),
если 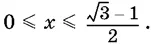
22.6.Докажите, что если 0 ≤ x ≤ 1, то
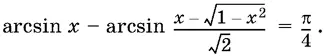
22.7.Докажите, что выражение arcsin 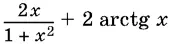 не зависит от x , если x < −1, и упростите его в этом случае.
не зависит от x , если x < −1, и упростите его в этом случае.
Решите уравнения:
22.8.tg (З arcsin x ) = 1.
22.9.arcsin 3 x / 5 + arcsin 4 x / 5 = arcsin x .
22.10.arcsin 2 x + arcsin x = π/ 3.
22.11.arctg (2 + cos x ) − arctg (2 cos² x / 2) = π/ 4.
22.12. 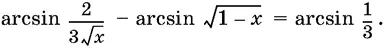
22.13.arctg ( x − 1) + arctg x + arctg ( x + 1) = arctg З x .
Глава 23
Область определения. Периодичность
Областью определения функции может быть вся числовая ось ( у = x ², у = sin x ), луч с принадлежащей ему граничной точкой ( у = √ x , граничная точка x = 0 принадлежит области определения x ≥ 0) и с не принадлежащей ему граничной точкой ( у = lg x ), совокупность интервалов (замкнутых, открытых, полуоткрытых) и отдельных точек.
Важной характеристикой функции является ее периодичность. С помощью периодических функций можно описать явления, повторяющиеся через равные промежутки времени. Функция f ( x ) называется периодической, если существует такое число T ≠ 0, что для любого значения аргумента x ч и ́сла x + T и x − T также являются значениями аргумента и выполняется равенство f ( x + T ) = f ( x ).
Если T — период f ( x ) и x — значение аргумента, то x + nТ , где n — целое число, — также значение ее аргумента, а пТ — период функции f ( x ). В частности, если T — период, то и − T — тоже период.
Наименьший положительный период называется основным периодом.
23.1.Найдите область определения функции 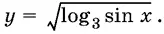
23.2.Найдите область определения функции
log 3log ½( x ² − x − 1).
23.3.При каких значениях x выражение 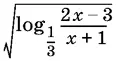 принимает действительные значения?
принимает действительные значения?
Читать дальше
Конец ознакомительного отрывка
Купить книгу

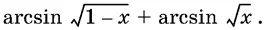
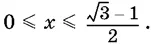
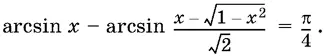
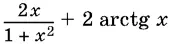 не зависит от x , если x < −1, и упростите его в этом случае.
не зависит от x , если x < −1, и упростите его в этом случае.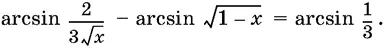
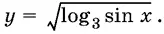
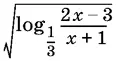 принимает действительные значения?
принимает действительные значения?










