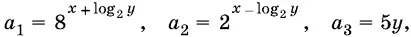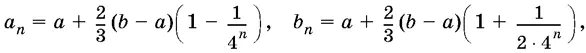19.5.Найдите сумму
S = 7 + 77 + 777 + ... + 777...7,
где последнее слагаемое содержит n цифр.
19.6.Докажите, что 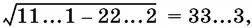 где цифра 1 повторяется 2 n раз, и цифры 2 и 3 только n раз.
где цифра 1 повторяется 2 n раз, и цифры 2 и 3 только n раз.
19.7.При каких значениях x и у последовательность а 1, а 2, а 3, где
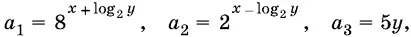
является одновременно арифметической и геометрической прогрессией?
19.8.Пусть х 1и х 2— корни уравнения x ² − 3 х + А = 0, а х 3и х 4— корни уравнения x ² − 12 х + В = 0. Известно, что последовательность х 1, х 2, х 3, x 4является возрастающей геометрической прогрессией. Найдите А и В .
19.9.Решите уравнение
х ³ − 7 х ² + 14 х + а = 0,
зная, что его корни образуют возрастающую геометрическую прогрессию.
19.10.В бесконечно убывающей геометрической прогрессии сумма всех членов вдвое больше суммы первых n членов. Найдите произведение первых n членов, если первый член равен √2.
19.11.Найдите трехзначное число, цифры которого образуют арифметическую прогрессию и которое делится на 45.
19.12.Найдите трехзначное число по следующим условиям: его цифры образуют геометрическую прогрессию; если из него вычесть 594, то получится число, записанное теми же цифрами, но в обратном порядке; если цифры искомого числа увеличить соответственно на 1, на 2 и на 1, то получится арифметическая прогрессия.
19.13.Имеющиеся в колхозе комбайны, работая вместе, могут убрать урожай за одни сутки. Однако по плану комбайны возвращались с других полей и вступали в работу последовательно: в первый час работал лишь один комбайн, во второй — два, в третий — три и т. д. до тех пор, пока не начали работать все комбайны, после чего в течение нескольких часов перед завершением уборки урожая действовали все комбайны. Время работы по плану можно было бы сократить на 6 ч, если бы с самого начала уборки постоянно работали все комбайны, за исключением пяти. Сколько было комбайнов в колхозе?
19.14.Три брата, возрасты которых образуют геометрическую прогрессию, делят между собой некую сумму денег пропорционально своему возрасту. Если бы они это проделали через 3 года, когда самый младший окажется вдвое моложе самого старшего, то младший получил бы на 105, а средний на 15 p. больше, чем сейчас. Сколько лет каждому из братьев?
19.15.Три отличных от нуля действительных числа образуют арифметическую прогрессию, а квадраты этих чисел, взятые в том же порядке, образуют геометрическую прогрессию. Найдите всевозможные знаменатели этой геометрической прогрессии.
19.16.Даны два числа а и b . Составим последовательность а , b , a 1, b 1, a 2, b 2, ..., а n , b n , ..., каждый член которой, начиная с третьего, равен среднему арифметическому двух предшествующих. Докажите, что
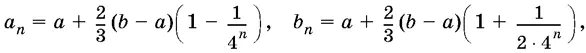
и найдите предел этой последовательности.
19.17.Найдите все положительные значения а , для которых все неотрицательные значения x , удовлетворяющие уравнению
cos [(8 а − 3) x ] = cos [(14 а + 5) x ]
и расположенные в порядке возрастания, образуют арифметическую прогрессию.
При решении задач, связанных с последовательностями, приходится доказывать утверждения такого типа: «Для любого целого n ≥ p (где p — целое) справедливо...»
Доказательство этих утверждений базируется на аксиоме индукции.
Пусть для некоторого утверждения А доказаны две теоремы.
Теорема 1.Утверждение А справедливо для n = p .
Теорема 2.Из условия, что утверждение А справедливо для всех p ≤ n ≤ k, следует, что оно справедливо для n = k + 1.
Тогда в качестве аксиомы (она называется аксиомой индукции) принимают, что утверждение А справедливо для всех n ≥ p ( n , p и А — целые числа).
Метод доказательства, основанный на использовании аксиомы индукции, называется методом математической индукции .
С помощью метода математической индукции можно доказать формулы
Читать дальше
Конец ознакомительного отрывка
Купить книгу

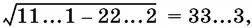 где цифра 1 повторяется 2 n раз, и цифры 2 и 3 только n раз.
где цифра 1 повторяется 2 n раз, и цифры 2 и 3 только n раз.