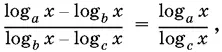18.18.Завод должен получить 1100 деталей. На базе имеются комплекты по 70, 40 и 25 деталей. Стоимость пересылки одного комплекта равна соответственно 20, 10 и 7 p. Какие комплекты и в каком количестве следует заводу заказать, чтобы расходы по пересылке были наименьшими? Переупаковка комплектов на базе не допускается.
Глава 19
Последовательности и прогрессии
Рассмотрим функцию натурального аргумента а n = f ( n ), где либо n = 1, 2, 3, ..., k , либо n = 1, 2, 3, ..., k , ... . Если при любых натуральных i и j , таких, что i < j , значение а j считается последующим по отношению к а i , то множество значений а n этой функции образует последовательность .
Последовательность обозначают, записывая ее члены а n один за другим в порядке возрастания номера n : а 1, a 2, а 3, ... .
Если номер n принимает значения n = 1, 2, 3, ..., k , то последовательность называется конечной. Если же n = 1, 2, 3, ... (т. е. n пробегает все натуральные числа), то последовательность называется бесконечной.
а n = f ( n ) называется общим членом последовательности. Если для любых i и j , таких, что i < j , выполняется неравенство а i < а j , то последовательность называется возрастающей. Если при тех же условиях будет а i > а j , то последовательность называется убывающей. Если же при любых i и j , таких, что i < j , выполняется неравенство а i ≤ а j ( а i ≥ а j ), то последовательность называется неубывающей ( невозрастающей ).
Последовательность, в которой
а i + 1= а i + d
при всех натуральных i , называется арифметической прогрессией. Число d называется разностью арифметической прогрессии. Имеют место формулы:
2 а n = а n + 1+ а n − 1; а n = а 1+ d ( n − 1);
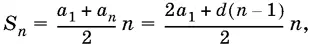
где S n — сумма n первых членов прогрессии.
Последовательность, в которой
a i + 1= qa i
при всех натуральных i , причем q ≠ 0 и a i ≠ 0, называется геометрической прогрессией , а число q называется ее знаменателем .
Для геометрической прогрессии имеют место формулы:
a n = a 1 q n − 1; 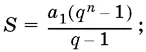 a ² n = a n − 1 a n + 1.
a ² n = a n − 1 a n + 1.
Вторая формула верна, если q ≠ 1. Бесконечная геометрическая прогрессия, у которой | q | < 1, называется бесконечно убывающей .
Бесконечно убывающая геометрическая прогрессия не обязательно является убывающей последовательностью. Она может быть возрастающей, например, при a 1= −1, q = ½ , а может быть колеблющейся: a 1= 1, q = −½ .
Если для бесконечной последовательности существует конечный предел последовательности ее сумм S n , т. е. существует 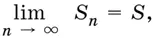 , то S называется суммой всех членов этой бесконечной последовательности.
, то S называется суммой всех членов этой бесконечной последовательности.
Для того чтобы бесконечная геометрическая прогрессия имела сумму всех своих членов, необходимо и достаточно, чтобы она была бесконечно убывающей. В этом случае
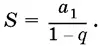
19.1.Общий член последовательности 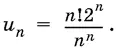 Является эта последовательность возрастающей или убывающей?
Является эта последовательность возрастающей или убывающей?
19.2.Докажите, что если члены a p, a q, a r, a s арифметической прогрессии образуют геометрическую прогрессию, то последовательность p − q , q − r , r − s является геометрической прогрессией.
19.3.Докажите, что если положительные числа a , b , с — соответственно m -й, n -й и p -й члены как арифметической, так и геометрической прогрессии, то
a b − сb с − aс a − b = 1.
19.4.Докажите, что если а , b , с образуют геометрическую прогрессию, то
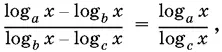
где x > 0, x ≠ 1, а , b , с — различные положительные числа, отличные от единицы.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

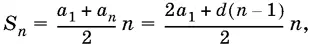
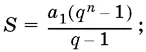 a ² n = a n − 1 a n + 1.
a ² n = a n − 1 a n + 1.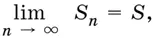 , то S называется суммой всех членов этой бесконечной последовательности.
, то S называется суммой всех членов этой бесконечной последовательности.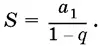
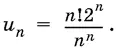 Является эта последовательность возрастающей или убывающей?
Является эта последовательность возрастающей или убывающей?