Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

7.2.Прежде чем выполнять действия в скобках, следует упростить дроби, разложив числители и знаменатели на множители.

7.3.Перед нами сумма из трех слагаемых. Если первые два привести к общему знаменателю, то в числителе произойдут существенные упрощения.

7.4.Прежде чем производить вычитание, следует упростить дробь.

7.5.Если вынести за скобки х 2 m , то в скобках останется x в степени, содержащей множителями m − n и 1/ mn . Это упростит дальнейшие преобразования. (!)

7.6.Каждое из подкоренных выражений является полным квадратом.

7.7.Обратить внимание на то, что

9 + 4√2 = 8 + 4√2 + 1 = (2√2 + 1)².

7.8.Каждую из вторых скобок разбить на два слагаемых x ² − u ² и z ² − у ², после чего собрать все члены, содержащие множитель x ² − u ², и все члены, содержащие z ² − у ². (!)

7.9.Если обозначить левую часть через z , то, освобождаясь от радикалов, можно получить уравнение относительно z .

7.10.Равенство, которое нужно доказать, представляет собой однородное выражение седьмой степени. Возвести в степень

а + b + с = 0 и а + b = − с .

7.11.Задача сводится к разбору случаев, позволяющих раскрыть знаки абсолютной величины. Количество рассматриваемых случаев можно уменьшить, если заметить, что равенство, о котором идет речь, не меняется при замене x на − x .

7.12.Можно разобрать различные случаи взаимного расположения чисел x , у и 0. Однако проще возвести каждую часть в квадрат. Так как обе части неотрицательны, то мы получим равенство, равносильное данному. (!)

7.13.Условие можно записать в виде а ⅓+ b ⅓= − с ⅓и возвести это соотношение в куб.

7.14.Данный трехчлен тождественно равен выражению

( ax + b )³ − ( сх + d )³, где а > 0, b > 0, с > 0, d > 0.

8.1.Поскольку выражения, стоящие в скобках, расположены симметрично относительно значения x = 5, удобно ввести новое неизвестное у = x − 5. После того как мы раскроем скобки, произойдут значительные упрощения. (!)

8.2.Можно перемножить скобки по две, чтобы получить квадратные трехчлены, отличающиеся только свободным членом.

8.3.Если записать уравнение в виде x ² − 17 = 3 у ², то возникает мысль доказать, что левая часть ни при каких целых x не делится на 3. (!)

8.4.Если целое у зафиксировать, то получим квадратное уравнение относительно x . Поэтому естественно обратить внимание на те ограничения, которые накладывает на у условие неотрицательности дискриминанта этого уравнения. (!)

8.5.Остаток следует искать в виде аx + b , а частное удобно обозначить через Q ( x ). Следуя определению деления, записать тождество.

8.6.Если переписать уравнение в виде

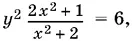
то благодаря условию целочисленности решений можно ограничить возможные значения у рассмотрением нескольких случаев.

8.7.Если подставить известный корень в уравнение, найти коэффициенты при рациональной и иррациональной частях, то получим систему двух уравнений для определения а и b .

8.8.Ответьте на вопрос: достаточно ли воспользоваться теоремой Виета, в силу которой свободный член и второй коэффициент должны быть положительными?

8.9.Если обозначить первый корень через x 1, а знаменатель прогрессии через q , то останется применить теорему Виета. (!)

8.10.С помощью теоремы Виета получить зависимость между α 1, α 2, α 3и коэффициентами данного уравнения. (!)

8.11.Разделить x ³ + аx + 1 на x − α по правилу деления многочлена на двучлен.

8.12.Ясно, что остаток нужно искать в виде аx + b . Если данный многочлен обозначить через P ( x ), а частное от его деления на ( x − 2)( x − 3) — через Q ( x ), то мы сможем воспользоваться определением деления многочленов.

8.13.Если многочлен x 4+ 1 разделится на x ² + рx + q , то в частном мы получим многочлен второй степени, т. е. x ² + аx + b .

8.14.Если данный многочлен делится на ( x − 1)³, то после замены x − 1 = у получим многочлен, который должен делиться на у ³.