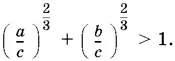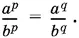Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

10.1.Из условия а + b = 2 следует, что числа а и b расположены симметрично относительно единицы. Использовать этот факт.

10.2.Условие а 1 а 2... а n = 1 можно использовать при преобразовании левой части неравенства, умножая или деля ее на произведение а 1 а 2... а n . Поскольку число множителей 1 + а i совпадает с показателем степени в правой части неравенства и все множители равноправны, то следует доказать, что каждый из них не меньше двух.

10.3. Способ 1.Поделить данное в условии равенство а + b = с почленно на с ⅓.

Способ 2.Доказать эквивалентное неравенство:

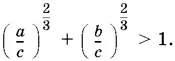
10.4.Избавиться от дробей и использовать условие 0 ≤ x ≤ 1. Это условие обеспечивает выполнение таких неравенств, как x k + 1 ≤ x k , 1 − x k ≥ 0 при любом натуральном k . (!)

10.5.Оценить каждый корень с помощью неравенства между средним геометрическим и средним арифметическим двух чисел, взяв в качестве первого числа подкоренное выражение, а в качестве второго единицу.

10.6.Предположить, что b ≤ а , и оценить левую часть данного неравенства, заменив b на а . (!)

10.7.Если бы между правой и левой частями стоял знак равенства, то мы имели бы производную пропорцию от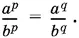

10.8.Воспользоваться неравенством между средним арифметическим и средним геометрическим двух чисел.

10.9. Способ 1.Если обозначить три положительных слагаемых в левой части неравенства через u , v и w , то uvw = 1. Следовательно, среди чисел u , v и w есть одно большее единицы и одно меньшее единицы, например, u > 1, v < 1. Тогда (1 − u )( v − 1) > 0.

Способ 2.Если u , v и w — положительные числа, причем w — наименьшее, то u > w , v > w . Неравенство v > w можно умножить на положительное число u − w и полученное неравенство разделить почленно на uw.

Способ 3.Если с < b < а , то можно записать, что b = с + d 1, а = b + d 2, где d 1и d 2— положительные числа. Подставьте в левую часть неравенства вместо а и b их выражения с + d 1и b + d 2— соответственно.

10.10.Преобразования удобно начать с записи S по формуле Герона. Величину S нужно оценить так, чтобы прийти к выражению, симметричному относительно а, b и с . Поскольку из четырех множителей p , p − а , p − b , p − с первый удовлетворяет этому требованию (2 р = а + b + с ), следует подвергнуть преобразованиям три других множителя. При этом полезно обратить внимание на то обстоятельство, что их сумма равна p :

p − а + p − b + p − с = 3 р − ( а + b + с ) = p .

10.11.Если перемножить крайние и средние скобки, то получатся два трехчлена, отличающиеся только свободным членом. Это позволяет оценить левую часть, выделив квадрат трехчлена, свободный член которого находится посередине между свободными членами первого и второго трехчленов. (!)

10.12.Данные уравнения симметричны относительно у и z и не симметричны (второе) относительно x . Если воспользоваться вторым уравнением и из первого выразить у + z через x , то мы получим простую систему относительно у и z , где x выступает в роли свободного члена.

10.13. Данные уравнения можно переписать в виде

у + z = 5 − x , yz + x ( z + y ) = 8,

после чего можно получить уравнение, корнями которого будут у и z , а коэффициенты будут зависеть от x .

10.14.Нужно рассмотреть три случая, в зависимости от того, положителен, отрицателен или равен нулю дискриминант трехчлена. Затем обратить внимание на знак старшего коэффициента. (!)

10.15.Так как коэффициент при x ² положителен, то ветви параболы направлены вверх. Рассмотреть возможное расположение корней параболы относительно отрезка 1 < x < 2.

10.16.Воспользоваться теоремой Виета и рассмотреть случаи, когда х 1и x 2одного знака и разных знаков.