10.17.Определить направление ветвей параболы и расположение ее корней относительно точек −1 и +1, чтобы условия задачи выполнялись.
10.18.Если m ≠ 0 (случай m = 0 следует рассмотреть отдельно), то ветви параболы у = mx ² − 4 x + 3 m + 1 должны быть направлены вверх.
10.19.Рассмотреть случаи, позволяющие раскрыть знаки абсолютной величины. Удобнее записать это неравенство как совокупность двух систем: в первой выражение, стоящее под знаком абсолютной величины, неотрицательно, а во второй системе оно отрицательно. (!)
10.20.Чтобы избавиться от знаков абсолютных величин, достаточно вспомнить о том, как они могли быть получены, например 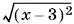 = | x − 3|. (!)
= | x − 3|. (!)
10.21.Чтобы упростить данное неравенство, его нужно умножить на 4 x . Поскольку результат будет зависеть от знака x , необходимо рассмотреть два случая: x < 0 и x > 0. (!)
10.22.Если перенести 3 в левую часть неравенства и привести полученное выражение к общему знаменателю, то получим дробь, которая должна быть отрицательной.
10.23.Неравенство можно упростить, если перенести все в одну сторону, привести выражения, стоящие под радикалами, к общему знаменателю и вынести за скобки неотрицательный множитель 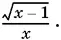
10.24.Удобно рассмотреть два случая: x > 0 и x < 0 (при x = 0 сразу видно, что неравенство не выполняется).
10.25.В неравенство входит сумма двух выражений: √ x , 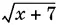 — и их удвоенное произведение. Кроме этого, в правой части стоит член −2 x , который после перенесения его в левую часть можно использовать для образования суммы квадратов этих выражений.
— и их удвоенное произведение. Кроме этого, в правой части стоит член −2 x , который после перенесения его в левую часть можно использовать для образования суммы квадратов этих выражений.
10.26.Поскольку второе слагаемое всегда неотрицательно, целесообразно рассмотреть два случая: x > 0 и x ≤ 0.
10.27.Если привести обе части неравенства к основанию 2, то можно заметить симметрию показателей.
10.28.Если перенести все влево и сгруппировать члены, содержащие иррациональное выражение в показателе степени, то это поможет разложить левую часть на множители. (!)
10.29.Придется разобрать два случая: x > 0 и x ≤ 0. Когда x > 0, данное неравенство равносильно такому:
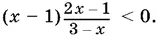
10.30.Чтобы сравнить показатели степени, необходимо выяснить, как основание расположено по отношению к единице.
10.31.Так как обязательно x > 0, то можно упростить неравенство, разделив обе его части на x .
10.32.При x > 0 получаем равносильное неравенство
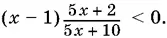
Что будет при x < 0?
10.33.При возведении в квадрат нужно потребовать, чтобы подкоренное выражение было неотрицательным. (!)
10.34.Выражение, стоящее под знаком логарифма, должно быть положительным . Абсолютная величина выражения неотрицательна . Как видите, это не совсем одно и то же. (!)
10.35.При решении логарифмических неравенств удобнее иметь дело с одинаковыми основаниями логарифмов. Если вы выбрали в качестве такого основания число 5, то обратите внимание на правую часть неравенства. Осуществив в ней почленное деление числителя на знаменатель, вы обнаружите, что 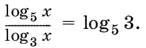 При этом появляются ограничения x > 0, x ≠ 1. Существенны ли они в процессе решения?
При этом появляются ограничения x > 0, x ≠ 1. Существенны ли они в процессе решения?
10.36.Перейти к одному основанию и получить под знаками логарифма одинаковое число. (!)
10.37.Неравенство легко приводится к виду
log | x + 6|( x ² − x − 2) ≥ 1. (!)
10.38.Если обозначить log а x = у, то получим простое неравенство относительно у .
10.39.Перейти к общему основанию k .
10.40.Вообще говоря, нужно рассмотреть случаи, когда основание x больше единицы и когда оно находится между нулем и единицей. Однако внимательное изучение данного неравенства позволяет рассмотреть только один из этих случаев.
10.41.Поскольку основание логарифма больше единицы, данное неравенство эквивалентно требованию, чтобы число, стоящее под знаком логарифма, было не меньше единицы.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

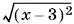 = | x − 3|. (!)
= | x − 3|. (!)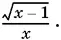
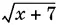 — и их удвоенное произведение. Кроме этого, в правой части стоит член −2 x , который после перенесения его в левую часть можно использовать для образования суммы квадратов этих выражений.
— и их удвоенное произведение. Кроме этого, в правой части стоит член −2 x , который после перенесения его в левую часть можно использовать для образования суммы квадратов этих выражений.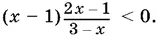
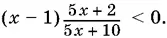
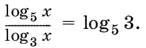 При этом появляются ограничения x > 0, x ≠ 1. Существенны ли они в процессе решения?
При этом появляются ограничения x > 0, x ≠ 1. Существенны ли они в процессе решения?










