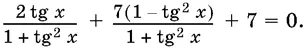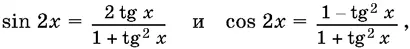Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Например, применение неабсолютного тождества [5] Под применением тождества мы понимаем замену его левой части на правую.

log x + log у = log xy

приводит к следствию, в то время как применение этого же тождества справа налево

log xy = log x + log у

может повлечь за собой потерю решений. В первом случае в результате замены log x + log у на log xy мы можем приобрести решения, лежащие в области x < 0, у < 0. Во втором случае решения из той же самой области могут быть потеряны.

При решении большинства уравнений угроза приобретения посторонних корней не должна нас пугать, так как в наших руках есть такое надежное средство, как проверка. Гораздо более опасной является перспектива потери корней.

Избежать потери корней можно, если вместо неабсолютных тождеств, сужающих область определения, пользоваться неабсолютными тождествами, расширяющими область определения уравнения.

Вернемся к рассмотренному только что примеру с суммой логарифмов. Когда при решении уравнения приходится потенцировать, то неабсолютное тождество

log x + log у = log xу

не приводит к потере корней. Если же по ходу преобразований возникла необходимость прологарифмировать произведение, то нужно воспользоваться другим неабсолютным тождеством

log xу = log | x | + log | у |,

применение которого может лишь расширить область определения уравнения.

Есть второй прием, позволяющий избежать потери решений, который мы поясним на примере уравнения: sin 2 x + 7 cos 2 x + 7 = 0. Воспользуемся формулами, позволяющими выразить sin 2 x и cos 2 x через tg x . Получим

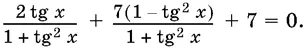
Приведя к общему знаменателю и отбросив знаменатель, который всегда отличен от нуля, получим простое уравнение

tg x = −7,

откуда x = −arctg 7 + π k , где k — любое целое число.

Хотя все произведенные преобразования кажутся «законными», мы легко убедимся в том, что целая серия корней x = π/ 2+ k π потеряна. Достаточно подставить эти значения неизвестного в исходное уравнение.

Корни были потеряны в результате применения неабсолютных тождеств

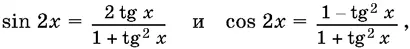
левые части которых существуют всегда, а правые теряют смысл

именно при x = π/ 2+ k π.

Если по каким-то причинам мы не могли избежать применения неабсолютных тождеств, грозящих потерей корней, то нам не остается ничего иного, как проверить те значения неизвестного, которые оказались исключенными из области определения входящих в уравнение выражений. В нашем примере, как и в большинстве тригонометрических уравнений, это нетрудно сделать.

Наконец, отметим такой важный момент при решении уравнений, как правильное использование условий.

Уравнение

lg (1 + x ) + 3 lg (1 − x ) = lg (1 − x ²) − 2

удобнее всего решать, преобразовав lg (1 − x ²) в сумму логарифмов. Чтобы оградить себя от возможной потери корней, мы должны написать

lg (1 − x ²) = lg |1 + x | + lg |1 − x |.

Однако подобная осторожность в этом примере является излишней. Поскольку в уравнение наряду с выражением lg (1 − x ²) входят lg (1 + x ) и lg (1 − x ), то 1 + x и 1 − x должны быть положительными, чтобы левая часть уравнения имела смысл. Поэтому вместо lg |1 + x | и lg |1 − x | можно написать lg (1 + x ) и lg (1 − x ). Таким образом, данное уравнение принимает вид

lg (1 + x ) + 3 lg (1 − x ) = lg (1 + x ) + lg (1 − x ) − 2.

Приведя подобные члены, получим

2 lg (1 − x ) = −2,

откуда x = 0,9 — единственный корень данного уравнения.

На этом примере мы видим, что правильное использование условия позволяет быстрее достичь цели, чем в случае чисто формальных преобразований.

Однако достаточно ли обоснованным было приведенное выше решение? Чтобы убедиться в этом, решите самостоятельно такое уравнение

lg (1 + x ) + 3 lg (1 − x ) = lg (1 − x ²) + 2.

Оно отличается от предыдущего лишь знаком последнего члена. Поэтому, повторив все приведенные только что рассуждения, получим

2 lg (1 − x )= 2,

откуда x = −9. Подставив это значение x в исходное уравнение, убеждаемся в том, что нами найден посторонний корень. Произошло это потому, что уравнения

lg (1 + x ) + 3 lg (1 − x ) = lg (1 + x ) + lg (1 − x ) + 2