§ 2. Конденсатор на больших частотах
А теперь обсудим подробнее поведение конденсатора — геометрически идеального конденсатора,—когда частота становится все выше и выше. Мы проследим за изменением его свойств. (Мы предпочли рассматривать конденсатор, а не индуктивность, потому что геометрия пары обкладок много проще геометрии катушки.) Итак, вот конденсатор (фиг. 23.4, а), состоит он из двух параллельных круговых обкладок, соединенных с внешним генератором парой проводов. Если зарядить конденсатор постоянным током, то на одной из обкладок появится положительный заряд, на другой — отрицательный, а между обкладками будет однородное электрическое поле.
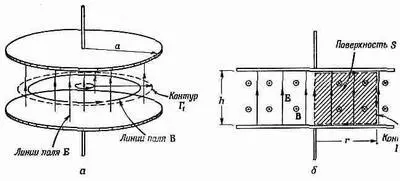
Фиг. 23.4. Электрическое и магнитное поля между обкладками конденсатора.
Представим теперь, что вместо постоянного тока к обкладкам приложено переменное напряжение низкой частоты. (После мы увидим, какая частота «низкая», а какая «высокая».) Конденсатор, скажем, соединен с низкочастотным генератором. Когда напряжение меняется, то с верхней обкладки положительный заряд убирается и прикладывается отрицательный. В момент, когда это происходит, электрическое поле исчезает, а потом восстанавливается, но уже в обратную сторону. Заряд медленно плещется туда-сюда, и поле поспевает за ним. В каждый момент электрическое поле однородно (фиг. 23.4, б); есть, правда, небольшие краевые эффекты, но мы намерены ими пренебречь. Величину электрического поля можно записать в виде
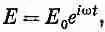
(23.2)

где Е 0 — постоянно. Но останется ли это справедливым, когда частота возрастет? Нет, потому что при движении электрического поля вверх и вниз через произвольную петлю Г 1проходит поток электрического поля (фиг. 23.4, а). А, как вам известно, изменяющееся электрическое поле создает магнитное. Согласно одному из уравнений Максвелла, при наличии изменяющегося электрического поля (как в нашем случае) обязан существовать и криволинейный интеграл от магнитного поля. Интеграл от магнитного поля по замкнутому кругу, умноженный на с 2, равен скорости изменения во времени электрического потока через поверхность внутри круга (если нет никаких токов):
(23.3)
Итак, сколько же здесь этого магнитного поля? Это узнать нетрудно. Возьмем в качестве петли Г 1круг радиуса r. Из симметрии ясно, что магнитное поле идет так, как показано на рисунке. Тогда интеграл от В равен 2prВ. А поскольку электрическое поле однородно, то поток его равен просто Е, умноженному на pr 2, на площадь круга:
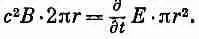
(23.4)
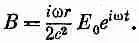
Производная Е по времени в нашем переменном поле равна iwE 0 e i w t , Значит, в нашем конденсаторе магнитное поле равно
(23.5)
Иными словами, магнитное поле тоже колеблется, а его величина пропорциональна w и r.
К какому эффекту это приведет? Когда существует магнитное поле, которое меняется, то возникнут наведенные электрические поля, и действие конденсатора станет слегка похоже на индуктивность. По мере роста частоты магнитное поле усиливается: оно пропорционально скорости изменения Е, т. е. w. Импеданс конденсатора больше не будет просто равен 1/i w С.
Будем увеличивать частоту и посмотрим повнимательнее, что происходит. У нас есть магнитное поле, которое плещется то туда, то сюда. Но тогда и электрическое поле не может, как мы раньше предполагали, остаться однородным! Если имеется изменяющееся магнитное поле, то по закону Фарадея должен существовать и контурный интеграл от электрического поля. Так что если существует заметное магнитное поле (а так и бывает на высоких частотах), то электрическое поле не может быть на всех расстояниях от центра одинаковым. Оно должно так меняться с r , чтобы криволинейный интеграл от него мог быть равен изменяющемуся потоку магнитного поля.
Посмотрим, сможем ли мы представить себе правильное электрическое поле. Это можно сделать, подсчитав «поправку» к тому, что было на низких частотах,— к однородному полю. Обозначим поле при низких частотах через Е 1 , и пусть оно по-прежнему равно Е 0 е i w t , а правильное поле запишем в виде
Читать дальше


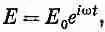

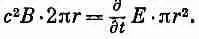
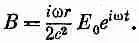



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
