Ричард Фейнман - 6a. Электродинамика

В самом деле, она выглядит так, как будто поле на высокой частоте все время старается обратиться в нуль где-то при с/w, примерно равном половине а. Давайте посмотрим, действитель­но ли функция J 0проходит через нуль и становится отрицатель­ной. Сперва испытаем х=2:

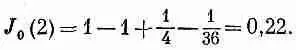
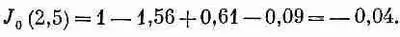
Это еще не нуль; но попробуем число побольше, скажем x=2,5. Подстановка дает

В точке x=2,5 функция J 0 уже перешла через нуль. Результаты при х=2 и при х=2,5 выглядят так, как будто J 0 прошла через нуль на одной пятой пути от 2,5 до 2. Поэтому надо проверить число 2,4:

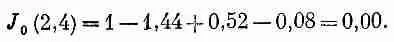
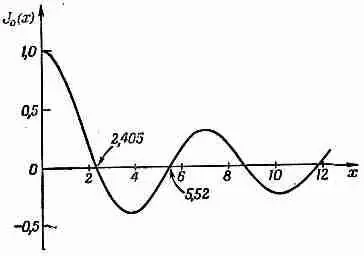
Фиг. 23.6. Функция Бесселя J 0(x).

С точностью до двух знаков после запятой получился нуль. Если рассчитывать точнее (или, поскольку функция J 0извест­на, если разыскать ответ в книжке), то обнаружится, что J 0" проходит через нуль при x=2,405. Мы провели расчет собствен­норучно, чтобы показать вам, что вы тоже способны открывать подобные вещи, а не заимствовать их из книг.

А если уж вы посмотрели про J 0в книжке, то интересно выяс­нить, как она идет при больших значениях х; она напоми­нает кривую на фиг. 23.6. Когда х возрастает, J 0(x) колеблется от положительных значений к отрицательным и обратно, по­степенно уменьшая размах колебаний.

Мы получили интересный результат: если достаточно увели­чить частоту, то электрические поля в центре конденсатора и у его края могут быть направлены в противоположные стороны. Например, пусть w так велико, что x=wr/с на внешнем краю кон­денсатора равно 4; тогда на фиг. 23.6 краю конденсатора отве­чает абсцисса x=4. Это означает, что наш конденсатор работает при частоте w=4с/а. И на краю обкладок электрическое поле будет довольно велико, но направлено не туда, куда можно было ожидать, а в обратную сторону. Эта ужасная вещь может про­изойти с конденсатором на больших частотах. При переходе к очень большим частотам электрическое поле по мере удаления от центра конденсатора много раз меняет свое направление. Кроме того, имеется еще связанное с этими электрическими по­лями магнитное поле. Не удивительно, что наш конденсатор при высоких частотах уже не напоминает идеальной емко­сти. Можно даже задуматься над тем, на что похож он силь­нее: на емкость или на индуктивность. Надо к тому же под­черкнуть, что на краях конденсатора происходят и более сложные эффекты, которыми мы пренебрегли. Например, там проис­ходит еще излучение волн за края конденсатора, так что настоя­щие поля куда сложнее тех, которые мы рассчитали. Впрочем, мы не будем сейчас заниматься этими эффектами.

Можно было бы, конечно, попробовать представить себе для конденсатора эквивалентную цепь, но, вероятно, будет лучше, если мы просто примем, что тот конденсатор, который мы сконструировали для низко­частотных полей, больше не го­дится, когда частоты слишком велики.

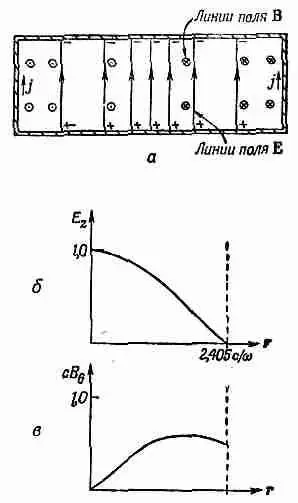
Фиг. 23.7. Электрическое и магнит­ное поля в закрытой цилиндрической банке.

И если мы хотим изу­чить, как действует такой объект на высоких частотах, нам нужно оставить те приближения к уравнениям Максвелла, которые мы делали, изучая цепи, и вер­нуться к полной системе уравне­ний, полностью описывающей поля в пространстве. Вместо того чтобы манипулировать о идеализированными элементами цепи, надо оперировать с реаль­ными проводниками, с такими, какие они есть на самом деле, учитывая все поля в пространстве между ними. Например, если нам нужен резонансный контур на высокие частоты, то не нужно пытаться его сконструировать с помощью одной катушки и плоского конденсатора.

Мы уже упомянули, что плоский конденсатор, который мы рассматривали, похож, с одной стороны, на емкость, а с другой— на индуктивность. От электрического поля возникают заряды на поверхностях обкладок, а от магнитного — обратные э.д.с. Не может ли оказаться, что перед нами уже готовый резонанс­ный контур? Оказывается, да. Представьте, что мы выбрали такую частоту, при которой картина электрического поля падает до нуля на каком-то расстоянии от края диска; иначе говоря, мы выбрали w a/с большим, чем 2,405. Всюду на окружности, центр которой лежит на оси обкладок, электрическое поле об­ратится в нуль. Возьмем кусок жести и вырежем полоску такой ширины, чтобы она как раз поместилась между плоскими обкладками конденсатора. Затем изогнем ее в форме цилиндра та­кого радиуса, на котором электрическое поле равно нулю. Раз там нет электрического поля, то по вставленному в конден­сатор цилиндру никаких токов не потечет, и ни электрические, ни магнитные поля не изменятся. Мы, стало быть, смогли закоротить друг на друга обкладки конденсатора, ничего не из­менив в нем. И посмотрите, что получилось: вышла настоящая цилиндрическая банка с электрическим и магнитным полями внутри, причем никак не связанная с внешним миром. Поля внутри не изменятся, даже если отрезать выступающие края обкладок и провода, ведущие к конденсатору. Останется только закрытая банка с электрическим и магнитным полями внутри нее (фиг. 23.7,а). Электрические поля колеблются то вперед, то назад с частотой w , которая, не забывайте, определила собою диаметр банки. Амплитуда колеблющегося поля Е меняется с расстоянием от оси банки так, как показано на фиг. 23.7,6. Кривая эта — просто первая дуга функции Бесселя нулевого порядка. В банке есть еще и круговое магнитное поле, которое колеблется во времени со сдвигом по фазе на 90° относительно электрического поля.