где E 2 — поправка из-за изменения магнитного поля. При любых w мы будем задавать поле в центре конденсатора в виде E 0 e i w t (тем самым определяя Е 0 ), так что в центре поправки не будет: E 2=0 при r=0.
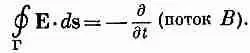
Чтобы найти Е 2 , можно использовать интегральную форму закона Фарадея
Интегралы берутся просто, если вычислять их вдоль линии Г 2, показанной на фиг. 23.4,б и идущей сперва по оси, затем по радиусу вдоль верхней обкладки до расстояния r, потом вертикально вниз на нижнюю обкладку и обратно к оси по радиусу. Контурный интеграл от Е 1 вдоль этой кривой, конечно, равен нулю; значит, в интеграл дает вклад только Е 2 , и интеграл равен просто — E z (r)h, где h — зазор между обкладками. (Мы считаем Е положительным, когда оно направлено вверх.) Это равно скорости изменения потока В, который получится, если вычислить интеграл по заштрихованной площади S внутри Г 2(фиг. 23.4,6). Поток через вертикальную полосу шириной dr равен B(r)hdr, а суммарный поток
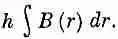
Полагая — d/dt от потока равным контурному интегралу от E 2, получаем
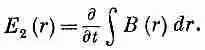
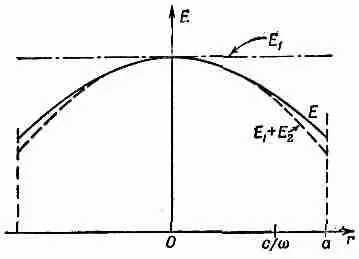
Фиг. 23.5. Электрическое поле между обкладками конденсатора на высоких частотах. Краевыми аффектами пренебрегли.
Заметьте, что h выпало: поля не зависят от величины зазора между обкладками.
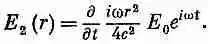
Используя для В(r) формулу (23.5), получаем
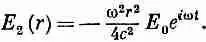
Дифференцирование по времени даст нам просто еще один множитель iw:
(23.7)
Как и ожидалось, наведенное поле стремится свести на нет первоначальное электрическое поле. Исправленное поле Е = Е 1 +Е 2 тогда равно
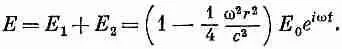
(23.8)
Электрическое поле в конденсаторе больше уже не однородно; оно имеет параболическую форму (штриховая линия на фиг. 23.5). Вы видите, что наш простенький конденсатор уже слегка усложняется.
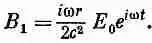
Наши результаты можно использовать для того, чтобы подсчитать импеданс конденсатора на больших частотах. Зная электрическое поле, можно подсчитать заряд обкладок и узнать, как ток через конденсатор зависит от частоты оз. Но эта задача нас сейчас не интересует. Нас больше интересует другое: что станется, если частота будет продолжать повышаться, что произойдет на еще больших частотах? Но разве мы уже не кончили наш расчет? Нет, потому что раз мы исправили электрическое поле, то, значит, магнитное поле, которое мы раньше подсчитали, больше уже не годится. Приближенно магнитное поле (23.5) правильно, но только в первом приближении. Обозначим его В 1, а (23.5) перепишем в виде
(23.9)
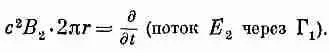
Вспомните, что это поле появилось от изменения Е 1. А правильное магнитное поле будет создаваться изменением суммарного электрического поля Е 1+Е 2. Если магнитное поле представить в виде В=В 1+В 2 , то второе слагаемое — это просто добавочное поле, создаваемое полем Е г .Чтобы узнать В 2, надо повторить все те же рассуждения, которые приводились, когда подсчитывали В 1: контурный интеграл от B 2вдоль кривой Г 1равен скорости изменения потока Е 2через Г 1. Опять получится то же уравнение (23.4), но В в нем надо заменить на В 2, а Е — на E 2:
Поскольку Е 2 с радиусом меняется, то для получения его потока надо интегрировать по круговой поверхности внутри Г 1. Беря в качестве элемента площади 2prdr, напишем этот интеграл в виде
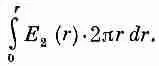
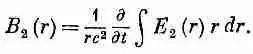
Читать дальше

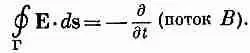
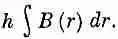
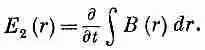

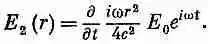
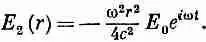
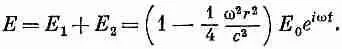
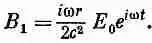
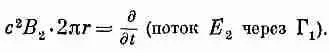
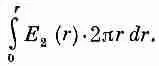
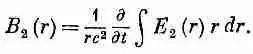



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
