Ричард Фейнман - 6a. Электродинамика

(22.33)

Заметьте еще, что, когда DL и D С стремятся к нулю, гранич­ная частота w 0=Ц4/LC уходит в бесконечность. У идеальной передающей линии нет граничной частоты.

§ 8. Другие элементы цепи

До сих пор мы определили только идеальные импедансы це­пи — индуктивность, емкость и сопротивление, а также идеаль­ный генератор напряжения. Теперь мы хотим показать, что дру­гие элементы, такие, как взаимоиндукция, или транзисторы, или радиолампы, можно описать, пользуясь теми же основными элемен­тами.

Фиг. 22.26. Эквивалент­ная схема взаимной индук­ции.

Пусть имеются две катушки, и пусть (это сделано нарочно или как-нибудь иначе) поток от одной из кату­шек пересекает другую (фиг. 22.26,а). Тогда возникает взаимная ин­дукция М двух ка­тушек, так что, когда ток в одной катушке меняется, в другой гене­рируется напряжение. Можно ли в наших эквивалентных контурах учесть такой эффект? Можно, поступив следующим образом. Мы видели, что наведенная в каждой из двух взаимодействующих катушек э. д. с. может быть пред­ставлена в виде суммы двух частей:

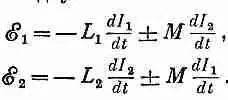
(22.34)

Первое слагаемое возникает из самоиндукции катушки, а второе — из ее взаимоиндукции с другой катушкой. Перед вторым слагаемым может стоять плюс или минус, смотря по тому, как поток от одной катушки пронизывает вторую. Делая те же приближения, как и тогда, когда мы описывали идеальную индуктивность, мы можем сказать, что разность потенциалов на зажимах каждой катушки равна э. д. с. катушки. И тогда оба уравнения (22.34) совпадут с теми, которые получились бы из цепи фиг. 22.26, б, если бы э. д. с. в каждом из двух начерченных контуров зависела от тока в противоположном контуре следую­щим образом:

(22.35)

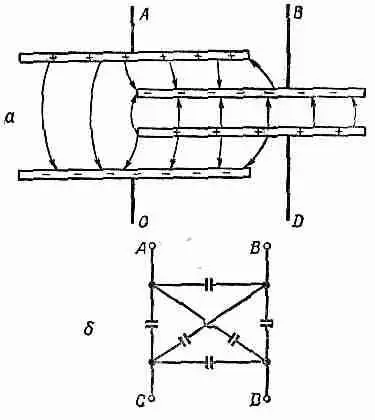
Фиг. 22.27. Эквивалентная схема взаимной емкости.

Значит, можно пред­ставить действие самоин­дукции нормальным обра­зом, а действие взаимной индукции заменить вспо­могательным идеальным генератором напряжения. Надо, конечно, иметь еще уравнение, связывающее эту з. д. с. с током в ка­кой-то другой части цепи; но, поскольку это урав­нение линейно, мы просто добавляем к нашим уравнениям цепи еще одно линейное уравнение, и все наши прежние выводы насчет эквивалентных схем и тому подобного все равно остаются правильными.

Кроме взаимной индукции, можно еще говорить и о вза­имной емкости. До сих пор, говоря о конденсаторах, мы всегда представляли, что у них только по два электрода, но во мно­гих случаях (скажем, в радиолампах) могут быть и по не­скольку электродов, расположенных вплотную друг к другу. Если на один из них поместить электрический заряд, то его электрическое поле наведет заряды на всех остальных электродах и повлияет на их потенциал. В качестве примера рассмотрим расположение четырех пластин (фиг. 22.27, а). Представим, что эти четыре пластины соединяются с внешней цепью провода­ми А, В, С и D. Так вот, пока нас интересуют только электро­статические эффекты, эквивалентную схему такого расположе­ния электродов можно считать такой, как на фиг. 22.27,6. Элект­ростатическое взаимодействие электродов (всякого со всяким) эквивалентно емкости между этой парой электродов.

И, наконец, посмотрим, как нужно представлять в цепях переменного тока такие сложные устройства, как транзисторы или радиолампы. Надо сначала подчеркнуть, что эти устройства часто действуют так, что связь между токами и напряжениями отнюдь не линейна. В этих случаях часть сделанных нами рань­ше утверждений, а именно те, которые зависят от линейности уравнений, естественно, перестают быть правильными. Но во многих приложениях рабочие характеристики в достаточной мере линейны — так что и транзисторы и лампы можно считать линейными устройствами.

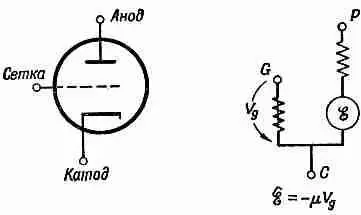
Фиг. 22.28. Низкочастотная эквивалентная схема вакуум­ного триода.