Нужно, однако, заметить, что из этого добавочного предположения вытекает интересное следствие: мы теряем при этом симметрию относительно времени, которая есть у уравнений Максвелла. Как исходные уравнения для Е и В, так и вытекающие из них волновые уравнения при изменении знака t не меняются. Эти уравнения утверждают, что любому решению, которое отвечает волне, бегущей в одну сторону, отвечает столь же правильное решение для волны, бегущей в обратную сторону. И утверждая, что мы намерены брать в расчет только расходящиеся сферические волны, мы делаем тем самым важное дополнительное предположение. (Очень тщательно изучалась такая электродинамика, в которой обходятся без этого дополнительного предположения. Как это ни удивительно, но во многих обстоятельствах она не приводит к физически абсурдным результатам. Однако обсуждение этих идей теперь увлекло бы нас чересчур в сторону. Мы поговорим об этом подробнее в гл. 28.)
Нужно упомянуть еще об одном важном факте. В нашем решении для расходящейся волны (20.35) функция ш в начале координат бесконечна. Это как-то необычно. Мы бы предпочли иметь такие волновые решения, которые гладки повсюду. Наше решение физически относится к такой ситуации, когда в начале координат располагается источник. Значит, мы нечаянно сделали одну ошибку: наша формула (20.35) не является решением свободного волнового уравнения (20.33) повсюду; уравнение (20.33) с нулем в правой части решено повсюду, кроме начала координат. Ошибка вкралась оттого, что некоторые действия при выводе уравнения при r=0 «незаконны».
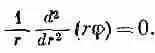
Покажем, что ту же самую ошибку легко сделать и в электростатике. Допустим, что нам нужно решить уравнение электростатического потенциала в пустом пространстве С 2j=0. Лапласиан равен нулю, потому что мы предположили, что никаких зарядов нигде нет. Но как обстоит дело со сферически симметричным решением уравнения, т. е. с функцией j, зависящей только от r? Используя для лапласиана формулу (20.32), получаем
Умножив это выражение на r, приходим к уже интегрировавшемуся уравнению
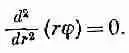
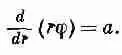
Проинтегрировав один раз по r , мы увидим, что первая производная rj равна постоянной, которую мы обозначим через а;
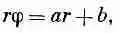
Еще раз проинтегрировав, мы получим для rj формулу
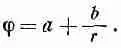
где b — другая постоянная интегрирования. Итак, мы обнаружили, что решение для электростатического потенциала в пустом пространстве имеет вид
Что-то здесь явно не так. Мы же знаем решение для электростатического потенциала в области, где нет электрических зарядов: потенциал всюду постоянен. Это соответствует первому слагаемому в решении. Но имеется еще и второй член, подсказывающий нам, что в потенциал дает вклад нечто, меняющееся как 1/r. Мы знаем, однако, что подобный потенциал соответствует точечному заряду в начале координат. Стало быть, хоть мы и думали, что нашли решение для потенциала в пустом пространстве, наше решение фактически дает нам также поле точечного источника в начале координат. Вы замечаете сходство между тем, что сейчас произошло, и тем, что произошло тогда, когда мы искали сферически симметричное решение волнового уравнения? Если бы в начале координат действительно не было ни зарядов, ни токов, то не возникли бы и сферически расходящиеся волны. Сферические волны должны вызываться источниками в начале координат. В следующей главе мы исследуем связь между излучаемыми электромагнитными волнами и вызывающими их токами и напряжениями.
Глава 21
РЕШЕНИЯ УРАВНЕНИЙ МАКСВЕЛЛА С ТОКАМИ И ЗАРЯДАМИ
§ 1. Свет и электромагнитные волны
§ 2. Сферические волны от точечного источника
§ 3. Общее решение уравнений Максвелла
§ 4. Поля колеблющегося диполя
§ 5. Потенциалы движущегося заряда; общее решение Льенара и Вихерта
§ 6. Потенциалы заряда, движущегося с постоянной скоростью;
формула Лоренца
Повторить: гл. 28 (вып. 3) «Электромагнитное излучение»; гл. 31 (вып. 3)
Читать дальше

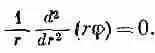
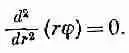
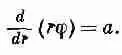
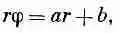
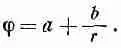



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
