Если некоторый объект движется, мы можем обозначить как x 1его координату в момент времени t 1и как x 2 – его координату в момент t 2. Представьте, что на самом деле это два события. Скорость нашего объекта такова: v = ( x 2− x 1)/( t 2− t 1) = Δ x /Δ t . В другой системе отсчета: V = ( X 2− X 1)/( T 2− T 1) = Δ X /Δ T . Мы можем воспользоваться преобразованием Лоренца, чтобы сравнить эти две величины. Обозначим буквой u относительную скорость двух СО, чтобы можно было использовать v и V для обозначения скорости объекта в каждой из двух систем. Запишем преобразование для двух событий и вычтем одно из другого:
Δ X = X 2− X 1= γ[( x 2− x 1) − u ( t 2− t 1)] = γ[Δ x − u Δ t ];
Δ T = T 2− T 1= γ[( t 2− t 1) − u ( x 2− x 1)/ c ²] = γ[Δ t − u Δ x / c ²].
А теперь разделим одно уравнение на другое, чтобы исключить γ:
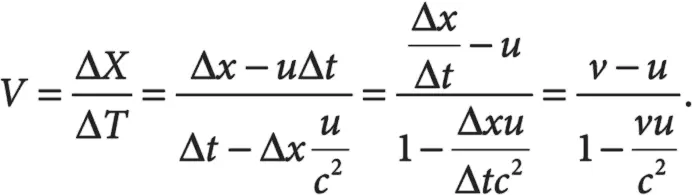
Это уравнение для преобразования скорости, позволяющее выразить скорость V во второй системе отсчета через v – скорость в первой системе отсчета.
Пусть v = c , то есть объект (к примеру, фотон) движется со скоростью света в первой СО. Во второй системе отсчета его скорость равна:
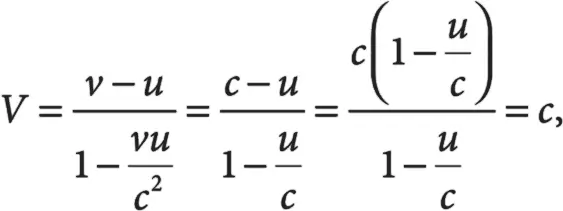
вне зависимости от u , относительной взаимной скорости двух систем отсчета. Если v = c , то V = c . Объекты, движущиеся со скоростью света в какой-то одной системе отсчета, движутся с той же скоростью и во всех остальных системах. Попробуйте подставить в уравнение v = − c и посмотрите, что получится. Удивлены?
Аналогичный вывод показывает, что c не меняется даже при произвольном направлении света [277].
Этот результат объясняет неудачу опыта Майкельсона−Морли в 1887 году, когда исследователи хотели обнаружить разницу скорости света в двух направлениях, первое из которых параллельно движению Земли, а второе – перпендикулярно этому движению.
Очень интересные вещи происходят, если два разделенных события близки по времени. Воспользуемся еще одним уравнением (взятым из приведенных выше рассуждений об одновременности):
Δ T = γ(Δ t − v Δ x / c ²) = γΔ t [1 − (Δ x /Δ t )( v / c ²)].
Определим ∆ x /∆ t = V E. Это псевдоскорость, которая «соединяет» два события. Записанное нами вовсе не означает, что чему-то действительно придется двигаться от одного события к другому; это просто скорость, с которой нужно было бы двигаться, чтобы присутствовать при обоих событиях. Может ли V Eбыть больше c ? Да, конечно. Любые два разделенных события, которые происходят одновременно, имеют бесконечную V E. Это не физическая скорость. Используя эту новую величину, мы можем записать:
Δ T = γΔ t (1 − V E v / c ²).
Будем считать для примера, что разность ∆ t положительна. Уравнение показывает, что ∆ T , в принципе, может быть и отрицательной. Для этого нужно всего лишь, чтобы отрицательное слагаемое в скобках было по модулю больше 1. Это означает, что в новой системе порядок событий может смениться на обратный. Такой результат может повлечь за собой самые разные следствия для причинной зависимости.
Чтобы V E v / c ² было больше единицы, V E/ c должно быть больше, чем c / v . Не забывайте, v – это скорость, связывающая две системы отсчета; она в любых обстоятельствах должна быть меньше c . Это означает, что c / v всегда будет больше единицы. Это уравнение говорит, что если V E/ c больше, чем c / v (что тоже делает его больше единицы), то порядок событий в двух системах отсчета меняется на обратный. Еще раз обратите внимание, что величина V Eничем не ограничена, поскольку это всего лишь псевдоскорость, призванная «соединить» два события, и что для двух сильно разнесенных в пространстве событий, но происходящих одновременно, величина V Eбудет бесконечна.
Математика парадокса шеста и сарая
Обратимся вновь к главе 4. В системе отсчета, связанной с сараем, шест входит концом в дверь и продолжает двигаться, пока не упрется в заднюю стену. Определим t 1= 0 как момент, когда передний конец шеста доходит до задней стены, и выберем систему координат так, что в этой точке x 1= 0. Из-за лоренцева сжатия в системе отсчета, связанной с сараем, задний конец шеста поравняется с дверью в этот же момент, при t 2= 0, в точке x 2= −6 м.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

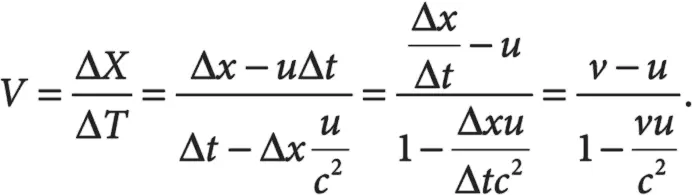
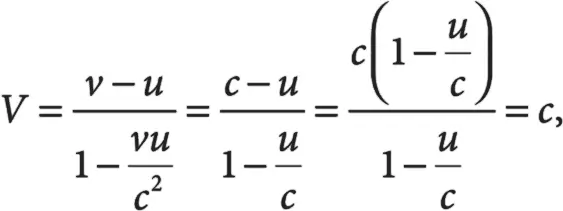






![Ричард Тукер - Гробница времени [Забытая палеонтологическая фантастика. Том XIV]](/books/407046/richard-tuker-grobnica-vremeni-zabytaya-paleontolog-thumb.webp)



